线性规划和网络流的单纯形法
线性规划
线性规划问题
求
网络流是线性规划的特殊形式。
在 \(m=m_1+m_2+m_3\) 个的前三约束中至少有 \(n\) 个约束以等号满足的可行解称为基本可行解。
线性规划基本定理：若线性规划存在最优解，则存在基本可行最优解。
上述定理的重要意义在于，它把一个最优化问题转化为一个组合问题。
若一个线性规划只有等号约束，称其具有标准形式。如果在每个等式中，至少有一个变量的系数为正，且变量只在此出现。这样的线性规划问题叫做约束标准型线性规划问题。
每个方程中找到一个这样的变量，称为基本变量，剩下的是非基本变量。
单纯形法
这样，问题被分成了两个部分：把线性规划转为约束标准型，求解约束标准型线性规划。
先解决约束标准型线性规划。
思路：求出一组解，经过调整（转轴）得到最优解。
先置所有非基本变量为 \(0\)，求出基本变量的解。
有所谓单纯形表，自行体会，，，
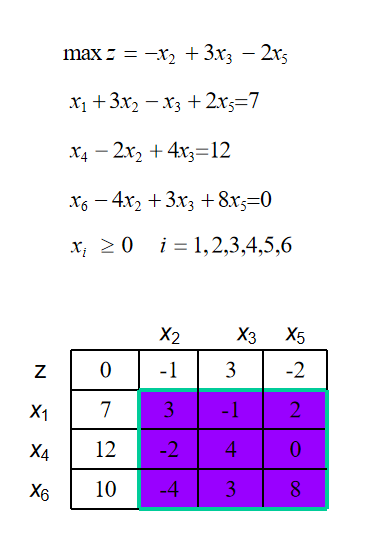
第一步：选出其增加也使目标函数增加的，下标最小的非基本变量作为入基变量。找不到则目前就是最优解。此处 \(x_3\) 对应系数是正数，符合条件。\(x_3\) 是入基变量。
第二步：考察限制入基变量的变量中最要紧的限制，让其离基。
如果入基变量所在列的所有元素都是负值，则目标函数无界，已经得到了问题的无界解。
受限的增加量可以用正的入基变量所在列的元素（称为主元素）去除主元素所在行的“常数列”（最左边的列）中元素而得到。所得到数值越小说明受到限制越要紧。
例如此处 \(x_3\) 入基，即要求找到最小的常数除以正对应列值。如果此最大值是负数，即没有限制，那么解无界。比方说，这里 \(x_1\) 主元素是负值不予考虑，\(x_4\) 对应 \(12/4=3\)，\(x_6\) 对应 \(10/3\)，\(3\) 是最小的，取 \(x_4\) 离基。
第三步：转轴变换。目的是执行入基、离基过程并修正单纯形表。
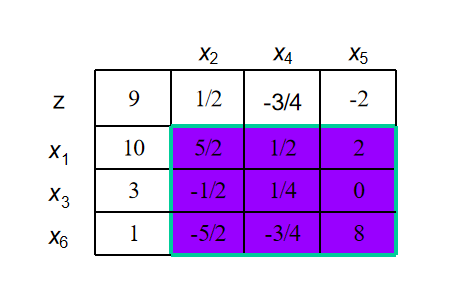
这就是转轴变换后的单纯形表。
对于离基变量的那个方程表示入基变量：
在其他行和目标函数消去 \(x_3\)，\(x_3\) 的位置变为 \(x_4\)。
第四步：返回第一步，递归知道得到无界或最优解。
转化方法
看起来，一般线性规划比约束标准型线性规划困难许多，但是我们现在声称这是等难的。
首先把不等式转为等式。每个不等式引入不影响答案的松弛变量即可：例如：
引入"人工基" \(z_i\)，把第 \(i\) 个等式约束加上 \(z_i\)。
采用大 \(M\) 法，即把答案变量的 \(z_i\) 系数设为 \(-\infty\)，来强制其在答案中为 \(0\)。
例题&代码 P3980
这里使用了对偶变换（也可以不）。
主要内容可见 link。
// Problem: P3980 [NOI2008] 志愿者招募
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3980
// Memory Limit: 125 MB
// Time Limit: 2000 ms
// UOB Koala'
//
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+5,maxm=1e4+5,INF=1e9;
int n,m;
int id[maxn+maxm];
#define db double
const db eps=1e-8;
db mp[maxm][maxn],b[maxm],*c=mp[0],ans[maxn+maxm];
//mp 是单纯形表
void pivot(int r,int c){//转轴
db coe=1/mp[r][c];
swap(id[n+r],id[c]);
mp[r][c]=1.0;
for(int i=1;i<=n;i++)mp[r][i]*=coe;
b[r]*=coe;
for(int i=0;i<=m;i++){
if(i==r)continue;
coe=mp[i][c];mp[i][c]=0.0;
for(int j=1;j<=n;j++)mp[i][j]-=coe*mp[r][j];
b[i]-=coe*b[r];
}
}
bool simplex(){
while(1){
int A=0,B=0;
db mn=INF;
for(int i=1;i<=n;i++)if(c[i]>c[B])B=i;//入基
if(!B)return 1;//找到解
for(int i=1;i<=m;i++){
if(mp[i][B]>eps&&b[i]/mp[i][B]<mn){
mn=b[i]/mp[i][B],A=i;
}
}
if(!A)return 0;//无界
// cout<<A<<" "<<B<<endl;
pivot(A,B);//A出基 B入基
}
}
signed main(){
// ios::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>c[i];
for(int i=1;i<=m;i++){
int l,r;cin>>l>>r>>b[i];
for(int j=l;j<=r;j++)mp[i][j]=1;
}
if(simplex())cout<<(int(-b[0]))<<endl;
return 0;
}
网络流单纯形
大概步骤是：
1.找到残量网络上的生成树（支撑树）
2.枚举边，判断支撑树加上这条边是否构成费用权的负环。不是，就枚举下一条边；否则进入 3。
3.将这条边入基，找到构成的负环上剩余流量最小的边出基。在这个过程中，将这个边推流，即把负环上所有边的流量加上这个值（最小的残量）。
4.继续枚举下一条边。重复 2~4 直到不可执行。
另外，为了满足线性规划的约束标准型，需要先从 \(T\) 向 \(S\) 连容量为 \(\infty\)，费用 \(-\infty\) 的边。
#include<bits/stdc++.h>
using namespace std;
#define int long long
namespace MCMF{
const int maxn=1e5+5,INF=1e9;
struct edge{
int u,v,f,w;
};
vector<edge> G;
void init(){
G.push_back({0,0,0,0});
G.push_back({0,0,0,0});
}
vector<int> E[maxn];
void add_edge(int u,int v,int f,int w){
G.push_back({u,v,f,w});
G.push_back({v,u,0,-w});
E[u].push_back(G.size()-2);
E[v].push_back(G.size()-1);
}
int pre[maxn],fa[maxn],fe[maxn],cir[maxn],tag[maxn];
int now=0,S,T;
void init_zct(int x,int e,int nod=1){
fe[x]=e,fa[x]=G[e].u,tag[x]=nod;
for(auto g:E[x]){
if(tag[G[g].v]!=nod&&G[g].f)init_zct(G[g].v,g,nod);
}
}
int sum(int x){
if(tag[x]==now)return pre[x];
tag[x]=now,pre[x]=sum(fa[x])+G[fe[x]].w;
return pre[x];
}
int push_flow(int x){
int rt=G[x].u,lca=G[x].v,cnt=0,del=0,P=2;
++now;
while(rt)tag[rt]=now,rt=fa[rt];
while(tag[lca]!=now)tag[lca]=now,lca=fa[lca];
int F=G[x].f,cst=0;
for(int u=G[x].u;u!=lca;u=fa[u]){
cir[++cnt]=fe[u];
if(F>G[fe[u]].f)F=G[fe[u]].f,del=u,P=0;
}
for(int u=G[x].v;u!=lca;u=fa[u]){
cir[++cnt]=fe[u]^1;
if(F>G[fe[u]^1].f)F=G[fe[u]^1].f,del=u,P=1;
}
cir[++cnt]=x;
for(int i=1;i<=cnt;i++)cst+=F*G[cir[i]].w,G[cir[i]].f-=F,G[cir[i]^1].f+=F;
if(P==2)return cst;
int u=G[x].u,v=G[x].v;
if(P==1)swap(u,v);
int lste=x^P,lstu=v,tmp;
while(lstu!=del){
lste^=1,--tag[u];
swap(fe[u],lste);
tmp=fa[u],fa[u]=lstu,lstu=u,u=tmp;
}
return cst;
}
int minc=0;
int simplex(){
add_edge(T,S,INF,-INF);
init_zct(T,0,++now);
tag[T]=++now,fa[T]=0;
bool run=1;
while(run){
run=0;
for(int i=0;i<G.size();i++){
if(G[i].f&&G[i].w+sum(G[i].u)-sum(G[i].v)<0)minc+=push_flow(i),run=1;
}
}
minc+=G[G.size()-1].f*INF;
return G[G.size()-1].f;
}
}
using MCMF::add_edge;
using MCMF::simplex;
using MCMF::minc;
using MCMF::S;
using MCMF::T;
int n,m;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;S=1,T=n;
MCMF::init();//Important!!1
for(int i=1;i<=m;i++){
int u,v,a,b;cin>>u>>v>>a>>b;
add_edge(u,v,a,b);
}
int f=simplex();
cout<<f<<" "<<minc<<endl;
return 0;
}
