代数学引论的 pdf 可以联系我要（

群，环，域

半群和幺半群

定义

对于一个映射 $*\mapsto X\times X\to X$，叫做 $X$ 上的二元代数运算。称 $(X,*)$ 为一个代数系统或代数结构。

对这样的运算，可以定义交换律和结合律。如果 $*$ 满足结合律，那么称 $(X,*)$ 是半群，有些时候只说 $X$。

单位元 $e\in X$ 是 $*$ 的单位元，当且仅当 $\forall x\in X,x*e=e*x=x$。显然，单位元不多于一个。

存在单位元的半群又叫做幺半群。

带有运算 $*$ 的半群 $X$ 的子集 $X'$ 称为 $X$ 的子半群，若 $\forall a,b\in S',a*b\in S'$。若单位元也在里面，则称为子幺半群。

例子

所有映射 $X\to X$ 构成幺半群 $M(X)$，运算为 $\circ$。$M(X)$ 的任意子幺半群叫做变换幺半群（好像在自动机里见过），

一个集合的所有子集和交或者并运算构成幺半群。

所有实矩阵和乘法或者加法构成幺半群，记作 $M_n(\R)$；$\R$ 实际上可以是一个交换环。

简单性质

若 $\cdot$ 结合，则 $x_1x_2x_3\dots x_k$ 添加括号与结果无关。

证明：

考虑归纳证明。

只需要证明

考虑归纳：

若 $\cdot$ 结合，对于若干相同元素乘起来定义方幂 $x^n$。若 $ab=e=ba$，称 $b=a^{-1}$。

根据上面结论：$x^mx^n=x^{m+n},(x^m)^n=x^{mn},\forall m,n\in \Z$。

不难归纳证明：

$\forall n\in \N,(xy)^n=x^ny^n,(xy)^{-n}=y^{-n}x^{-n}$。

群

全体元素可逆的幺半群叫做群。

同样有子群和真子群。

一个群的任意子群交起来也是其子群，这一结论可以扩展到环、域上。

例子和性质

特殊群

$GL_n(\R)$ 是行列式不为 $0$ 的 $n$ 阶实方阵，$SL_n(\R)$ 是行列式为 $1$ 的 $n$ 阶实方阵。根据线性代数中 $\det A\times B=\det A\times \det B$ 的结论，这是群。

$S(X)$ 称作对称群，是 $X$ 全体置换的群，乘法是复合。

群 $G$ 是循环群，当且仅当 $\exists g\in G,\text{s.t. }\forall a\in G,\exists n,a=g^n,n\in \Z$。可以简记为 $\left \langle a \right \rangle$。

在循环群中，$\forall m,n\in \Z$，

由于存在逆元，所以导致了不同（$m,n\in \Z$）。而此结论是容易证明的。

若 $a\in G$，设 $q$ 是满足 $a^q=e$ 的最小正整数。如果不存在，称 $a$ 是无限阶元，否则称 $q$ 是 $a$ 的阶。

容易根据上面的方幂法则证明 $\left\langle a\right\rangle=q$。

同构和同态

两个群 $(G,*),(G',\circ)$ 同构当且仅当存在双射 $f\mapsto G\to G'$，满足

此时称 $f$ 是同构。如果去掉双射条件，称 $f$ 是同态（存在一些平凡同态）。

同构的单位元对应，逆元对应。其逆映射也是同构。

任何同阶循环群同构，只需构造 $f(g^k)=g'^k$ 即可。

凯莱定理：任何群 $G$ 和其对称群 $S_G$ 的某个子群同构。

设 $L_a(g)=ag$，由于群的性质这是置换；构造 $f(a)=L_a$ 即可。

$G'=G$ 时的同构称为自同构。自同构群 $Aut(G)$ 是 $S_G$ 的子群。

同态 $f$ 的核 $\ker f=\{g\in G\mid f(g)=e'\}$ ，其中 $e'$ 是 $G'$ 的单位元。

不难证明， $\ker f$ 是 $G$ 的子群。

例子：$GL_n(\R)$ 到 $\R$ 乘法群的一个同态是 $f:=\det$。而 $SL_n(\R)=\ker f$。

$Aut(G)$ 甚至 $\varphi \in Aut(G)$ 都可能带来 $G$ 的重要信息。

例子：设 $G$ 有限，存在一个自同构 $\varphi$ 满足没有非单位元的不动点，且 $\varphi^2=1$，$\varphi(a)a^{-1}=\varphi(b)b^{-1}$。

此时，可以证明：$G$ 是阿贝尔群。

环和域

定义

在 $R$ 上定义两种运算（加法和乘法），满足：

$(R,+)$ 是阿贝尔群，$(R,\cdot)$ 是半群，$\cdot$ 对 $+$ 有左右分配律。

则称 $R$ 是环。

若 $(R,\cdot)$ 是幺半群，称此环具有单位元，若 $(R,\cdot)$ 是交换半群，则称此环是交换环；若 $(R-\{0\},\cdot)$ 是群，则称此环是除环（可以除法）。这里不叫阿贝尔环（？）

子环需要满足同时是加法的子群和是乘法的子半群。

域是交换除环。

例子和性质

环

$M_n(\R)$ 是环，更进一步地， $M_n(R)$ 是环，其中 $R$ 是交换环。

对于分配律，有广义分配律：

对于交换环，牛顿二项式定理（对于整数）成立。

剩余类环是模 $m$ 意义下的剩余类和模意义加法乘法构成的环。

环的同构 $f$ 需要同时满足加法和乘法的条件。此时，有 $f(0)=0',f(na)=nf(a),\forall n\in \Z$。

不难证明，环的核 $\ker f=\{a\in R\mid f(a)=0'\}$ 是 $R$ 的子环。

如果 $a,b\in R,a,b\neq 0,ab=0$，$a,b$ 称为左、右零因子。如果一个环无零因子且 $1\neq 0$，那么 $R$ 称为整环。

有单位元的非平凡交换环是整环当且仅当 $\forall a,b,c\in R$，

环上容易定义可逆元素。在有单位元的环 $R$ 上，全体可逆元素构成群。

以上结论证明是容易的。

域

域上可以定义分式：当 $b\neq 0$ 的时候，$ax=b$ 的唯一解是 $x=ba^{-1}$，记作 $\dfrac ab$。

分式的运算规则是我们知道的：下面证明

设 $x=a/b,y=c/d$。

域可以定义子域，要求其子环是域。比如，$\Q\subset \R$。

当域 $F\subset P$ 时，称 $P$ 是 $F$ 的扩域。若 $a\in P,a\not\in F$，取 $P$ 中所有包含 $\{a\}\cup F$ 的子域的交 $F_1$，则显然 $F_1$ 是包含 $\{a\}\cup F$ 的最小子域，记为 $F(a)$。在 P5320 一题中，即应用了 $\Z_{998244353}(\sqrt 5)$ 这个 $\Z_{998244353}$ 的扩域。

$\Z_p$ 是域当且仅当 $p$ 是素数。根据裴蜀定理及其逆定理知道。

$p\in\mathcal P,\Z_p$ 上注意到 $\{m,2m,\dots,(p-1)m\}=\{1,2,\dots,p-1\}$，且 $\Z_p$ 是整环，可证明费马小定理。

如果一个域不包含任意真子域，则称其为素域。

一个域 $P$ 包含且只包含一个素域 $P_0$。证明：如果有两个不同的素域，那么其交也是不同于它们的素域。矛盾。显然 $P_0$ 也是所有子域的交。

$P_0\simeq \Q$ 或 $\Z_p,p\in\mathcal P$。

证明：考虑映射 $f\mapsto \Z\to P$，$f(n)=n\cdot1$。显然 $f$ 是同态，$\ker f=m\Z$。且 $m\in \mathcal P\cup \{0\}$。

若 $m=0$，显然 $P_0\simeq \Q$；否则考虑 $\hat f(k)=(k\bmod m)\cdot 1$。$P_0\simeq \Z_m$。

此时称 $m$ 为 $P$ 的特征，记作 $char P=m$。

例子：证明域 $Q(\sqrt 2)$ 和 $Q(\sqrt 3)$ 不同构。

设存在同构 $f\mapsto Q(\sqrt 2)\to Q(\sqrt 3)$。

设 $f(\sqrt2)=\alpha$，则 $f(2)=\alpha^2$。而 $f(0)=0$，$f(1)=f(1\times 1)=f(1)^2$。在 $Q(\sqrt 3)$ 内 $f(1)$ 只有 $0,1$ 两个解，不能为 $0$，故 $f(1)=1,f(2)=2=\alpha^2$。而 $\alpha$ 在 $Q(\sqrt 3)$ 内无解，矛盾。

多项式和复数

复数域

引入和构造

是一个大家都知道的方程。我们可以把解记为 $\pm\sqrt{-1}$。问题是，这样的 $\sqrt{-1}$ 有什么意义。

我们希望把 $\R$ 加以扩张，使得新域中这个方程有解。

我们用一个同构的域来考虑它：

这样的 $2$ 阶方阵的集合记作 $P$。不难验证，$P$ 及矩阵加法乘法是域。

而令

则

我们知道域 $P$ 有子域 $P'=\{aE\mid a\in \R\}\simeq \R$。

而注意到

中 $J\in P$ 在同构意义下，就是这个 $\sqrt{-1}$，而 $P\simeq \C,P'\simeq \R$。

因而无需神秘地将 $J$ 当作“虚构的量”。

这样，没有任何神秘的东西，无需假设，我们找到了和复数域同构但是复数域 $\C$ 是一个和 $P$ 同构的域。$\C=\{(x,y)\mid x,y\in \R\}$。运算等不再赘述。

不难验证若干域的公理。现在，我们写下 $x+iy$ 的表达。同构意义下 $\Q\subset \R\subset \C$。

一些复数的知识已经被我们知道，不再重复。

简单性质

唯一性定理：

$\R$ 上任意二维向量空间 $K$，如果还是结合、交换、具有单位元且无零因子的环，则 $K\simeq \C$。

核心思想是找到 $j^2=-1$。

不妨认为 $\R\subset K$。设 $e\in K-\R$ 和 $1$ 构成一组基。那么可设 $e^2=\alpha\cdot 1+2\beta\cdot e$，其中 $\alpha,\beta\in \R$。设 $f=e-\beta\not\in \R,f^2=\gamma\in \R$。此处如果 $\gamma>0$，否则 $f\in \R$。那么 $\exists \delta\in\R,\text{s.t. }\delta^2=-\gamma^{-1}$。此时令 $j=\delta f$ 即可。找到之后构造映射 $\varphi :\C\to K,\varphi(x+iy)=x+jy$。

二次域 $\Q(\sqrt{d}),d\in \Z$ 是 $\C$ 的子域。不难证明这样的数是所有 $\alpha=a+b\sqrt{d},a,b\in\Q$。

这样的数的范数是 $N(\alpha)=a^2-db^2=\alpha f(\alpha)$。

范数在一定意义下可以代表原数：$N(\alpha)=0\iff \alpha =0,N(\alpha\beta)=N(\alpha)N(\beta)$。

有一个有趣的域是 $\C$ 的子域：$CS$，可构作域。这个域由从 $(0,0)$ 和 $(1,0)$ 出发，平面上可以尺规构作的点得到。

注意到一个点 $(x,y)$ 可构作等价于 $(0,y)$ 和 $(x,0)$ 可构作。通过相似三角形和四点共圆，可以构作数轴上的积和商（就可以构作两复数乘积）；而显然和是可构作的。这样就证明了是子域。此域的子域一般被称作可构作数域。

多项式环

定义

设 $R$ 是带单位元的交换环，$A$ 是某个子环。对于 $t\in R$，$R$ 中包含 $A,t$ 的最小带单位元子环的元素形如：

我们把这个这个新的交换环记为 $A[t]$。我们关心系数：元素可以记为 $(a_0,a_1,a_2,\dots)$。元素叫多项式。

事实上，我们不关心 $t$。所以把 $t$ 改为一个符号 $X$。这只是一个符号。不一定 $\in R$。

可以定义多项式的度数 $\deg$。$0$ 的度数记为 $-\infty$。

多项式乘法和加法的法则是我们知道的，可以验证其构成交换环。

可以定义同构 $\varphi :\varphi(a)=(a,0,0,\dots)$，而 $\{a,0,0,\dots\}$ 是 $A[X]$ 的子环。所以可以认为 $A\subset A[X]$。

不难定义多变元多项式，但是这里我们只讨论单变元多项式。

性质

当且仅当 $f,g$ 最高项系数乘积不为 $0$，$\deg fg=\deg f+\deg g$。

所以，$A[X]$ 是整环，当且仅当 $A$ 是整环。

到现在，我们还不知道多项式和我们一般的多项式函数有什么关系；这个 $X$ 不过是个符号。但是 $X$ 也可以有“$=t$ 时 $f$ 的值”。原因：

设交换环 $A\subset R$，$\forall t\in R$，存在唯一的同态 $\Pi_t:A[X]\to R$，使得：

证明：首先假设此同态存在。

由于 $\Pi_t(X)=t,\Pi_t(X^a)=t^a$，

不难发现此同态满足同态性质，由于广义分配律。

下面记 $\Pi_t(f)=f(t)$，称为 $f$ 在 $X=t$ 时的值。

令 $x\in A$，$\Pi_x$ 乃是联系多项式研究的函数观点和代数观点的一个纽带。

$t\in R$ 称为 $A$ 上的代数元，若 $\exists f\in A[X],f(t)=0$。若 $\Pi_t$ 是一个单射，则称 $t$ 是 $A$ 上的超越元。

当 $A=\Q,R=\C$ 时，我们叫代数数和超越数。

带余除法

设 $A$ 是整环，$g\in A[X]$，首项可逆。那么

且此 $q,r$ 唯一。

证明：

设

如果 $n<m$ 是平凡的。

归纳。边界条件不难验证。考虑消掉 $f$ 的第一项。

根据归纳假设，$\overline f=\overline qg+r$。

令

这样就找到了 $q,r$。

证明唯一性。设 $qg+r=q'g+r'=f$。

$(q-q')g=(r-r')$。根据 $A[X]$ 是整环，$q=q',r=r'$。

因式分解和整除

设 $R$ 是整环，定义整除关系 $a\mid b$，若存在 $c\in R,b=ac$。

若 $a\mid b$ 且 $b\mid a$，$a,b$ 称为相伴元，此时 $b=ua$，$u\mid 1$。

$p\in R$ 称为素元，若 $p\not\mid 1$，且 $\not\exists a,b\not\mid 1,p=ab$。$R[X]$ 的素元称为既约多项式。

下面给出几项性质：

较为显然。

整环 $R$ 叫做唯一因子分解环，若 $\forall a\in R$，

其中 $u\mid 1$，$p_1,p_2,\dots ,p_r$ 是素元（不必不等）。且如果

那么 $r=r'$，且存在 $r$ 阶排列 $\pi$，使得 $\forall i\in \Z\cap [1,r],p_{\pi_i}=u_ip'_{i}$，$u_i\mid 1$。

环上的：一个每个元素都有素因子分解的整环是唯一因子分解环，当且仅当每个整除 $ab(a,b\in R)$ 的素元 $p\in R$ 一定整除 $a$ 或 $b$。

先证前者推出后者。

设 $ab=pc$，

是 $a,b,c$ 的素因子分解。则 $\prod a_i\prod b_j=p\prod c_k$ 代表 $p$ 一定相伴于某个 $a_i$ 或者 $b_j$。那么 $p\mid a$ 或 $p\mid b$。

再证 后者推出前者。

归纳法。设 $n$ 个素元乘起来满足条件。

这里 $m\ge n$。

则 $p_{n+1}$ 应该是某个 $r_i$ 的因子。不妨认为是 $r_{m+1}$ 的。$r_{m+1}=up_{n+1},u\mid 1$。

两边去掉最后一个，根据归纳假设即证。

$\gcd$ 和 $\operatorname{lcm}$ 在环上是可以定义的（尽管环上不一定有序）。

设 $R$ 是整环，$a,b\in R$，$\gcd(a,b)$ 是这样的元素（相伴意义下）$d$：$d\mid a,b$，且 $c\mid a,b\Rightarrow c\mid d$。

$\operatorname{lcm}(a,b)$ 类似，是这样的 $d$：$a,b\mid d$，且 $a,b\mid c\Rightarrow d\mid c$。

不难证明：

且满足结合律、交换律。

$a,b\neq 0,m=\operatorname{lcm}(a,b),ab=dm\Rightarrow d=\gcd(a,b)$。

证明：验证两条定义即可。

若 $\gcd(a,b)=1$，称 $a,b$ 互素。

（写到这里突然忘了整环是交换环，没绷住）

整除性判别法：

在唯一因子分解整环中，认为所有因子取自相同素元（可能出现 $0$ 指数），$a\mid b$ 当且仅当 $a$ 的每个素元的指数都小于等于 $b$ 的。$\gcd$ 即取 $\min$,$\operatorname{lcm}$ 即取 $\max$。

我们知道整数求 $\gcd$ 有辗转相除法。我们尝试扩充他的使用范围。首先，必须可以带余除法；然后，这一过程必须有限。于是，诞生了欧几里得环的辗转相除法。

设 $R$ 是一个整环，存在一个映射

使得：

且 $\delta(r)<\delta(b)$ 或 $r=0$。

这样的 $\delta$ 保证了递降。

比方说，在 $P[X]$ 上，不难构造 $\delta=\deg$。

则称 $R$ 是欧几里得环（欧氏环）。在这样的环上，可以进行辗转相除法。

注意辗转相除法的过程，得到以下定理：

在欧式环 $R$ 中，任意两个数 $a,b$ 都有 $\gcd,\operatorname{lcm}$。并且 $\exists u,v\in R$，使得

特别地，

推论：

证明是不困难的。

欧氏环是唯一分解环。

先证存在分解。利用 $b=qa+r$ 不难证明，若 $b$ 是 $a$ 的真因子且不相伴，$\delta(a)>\delta(b)$。于是显然存在因子分解。

只需证明： $p\mid bc,p\in \mathcal P\Rightarrow p\mid b\lor p\mid c$。

设 $d=\gcd(b,p)$，则 $d$ 和 $1$ 或 $p$ 相伴。由上推论得知正确。

这样，我们证明了算术基本定理（在所有欧氏环中）。

既约多项式

重申定义：不能被任何度数更小的度数大于零的多项式整除的多项式。

依靠定义，一次多项式总是既约的。

下面，可以认为首一多项式分解出来一定是首一多项式，如果不是，其首项显然可逆，化为首一多项式即可。

任意域上的首一多项式有无限多。

仅考虑有限域。设得到了所有首一既约多项式 $p_1,p_2,\dots p_n$。而 $1+\prod p_i$ 显然是新的首一既约多项式或存在新的既约多项式因子。

由于有限域的一定次数的多项式有限，所以有限域上存在任意高次既约多项式。

设 $f=a_0+a_1X+\dots a_nX^n$ 容度 $d(f)=\gcd(a)$。

高斯引理：设 $R$ 是唯一因子分解环，$f,g\in R[X]$，则

在相伴意义下。

只需证明：本原多项式的积是本原多项式（容度为 $1$ 的多项式）。

设

设存在素元 $p$ 整除 $d(fg)$。选择最小下标 $s,t$，使得 $p\not\mid a_s,p\not\mid b_t$。这样的下标是存在的。

那么 $[X^{s+t}]fg$ 只有 $a_sb_t$ 项不含整除 $p$ 的乘数。而 $p\mid [X^{s+t}]fg$。那么 $p\mid a_sb_t$。那么 $p\mid a_s\lor p\mid a_t$，矛盾。

根据此引理，$\Z[X]$ 上的既约多项式在 $\Q[X]$ 上既约。反证即可。

艾森斯坦判别法：

设

是 $\Z$ 上的首一多项式。若 $p\mid a_1,a_2,\dots a_n,p^2\not\mid a_n$，则 $f(X)$ 在 $\Q$ 上既约。

设

在模 $p$ 意义下做这个。

得到所有 $b_i,c_i$ 应为 $0$。

此时 $s_n=a_sb_t$，整除 $p^2$，矛盾。

例子：

在 $\Q$ 上既约。

证明：

注意到等价于 $f(X+1)$ 既约即可。而 $f(X+1)$ 适用艾森斯坦判别法。

整环的分式域

我们已经知道，在域上有分式。但是整环也可以扩充出一个域，由分式构成。

设 $R$ 是整环。容易发现，$(a,b),a\in R,b\in R-\{0\}$ 在等价关系下的等价类和 $\dfrac{a}{b}$ 那些熟悉的运算规则构成了域。等价关系：$(a,b)$ 和 $(c,d)$ 等价当且仅当 $ad=bc$。这样的域记为 $Q(R)$，叫做分式域。可以认为 $R\subset Q(R)$。

不难证明，当 $P$ 是域时，$P\simeq Q(P)$。

设 $P$ 是域，$Q(P[X])$ 记为 $P(X)$，叫做 $P$ 的有理函数域。

有理函数 $f/g$ 的次数是 $\deg f-\deg g$。若 $\deg f/g<0$，称为真分式。

任何有理函数都可以唯一地表示成一个多项式和一个真分式的和。

证明：带余除法即可。容易证明唯一性。

最简分式：$f/g\in P(X)$ 称为最简的，如果 $g=p^n,n\ge 1,p\in p[X]$ 是既约多项式，且 $\deg f<\deg g$。

有理函数基本定理：

真分式可以唯一地表示为最简分式的和。

证明：

设 $f/g$ 是给定的真分式，不妨设 $g$ 是首一的。

引理 $1$：设 $g=g_1g_2$ 是两个互素的首一多项式乘积，那么：

且右侧两个分式是真分式，且唯一。

证明：

可以找到 $1=u_1g_1+u_2g_2$。那么 $f=fu_1g_1+fu_2g_2$。

设 $fu_2=qg_1+f_1$（带余除法），$f_2=fu_1+qg_2$，那么 $f=f_1g_2+f_2g_1$。

那么用 $g_1g_2$ 除就得到了原式。根据构造，$f_1/g_1\in P_0(X)$（真分式环），而 $f_2/g_2=f/g-f_1/g_1$，是真分式。

证明唯一是不难的（$g_1,g_2$ 互素）。

引理 $2$：设 $g$ 有分解

其中 $p_i$ 是两两不同的首一既约多项式。

则存在唯一确定的表达式：

其中 $f_i/p_i^{n_i}$ 是真分式（又叫准素分式）。

用引理 $1$ 归纳即可。

我们可以开始证明原定理：只需证明，所有真准素分式 $a/p^n$ 都可以唯一表示为最简分式之和。

不断做带余除法（已知 $\deg a<n\deg p$）：

所以：

这显然是唯一的。

证毕。

多项式的根

根和插值

定义

设 $A$ 是带单位元的交换环，$A\subset R$，$R$ 是整环。

定义多项式 $f\in A[X]$ 的根 $c\in R$，若 $f(c)=0$。注意根可以在某多项式所在域的扩域中。

Bezout 定理：元素 $c\in A$ 是 $f\in A[X]$ 的根，当且仅当 $(X-c)\mid f$。

证明：做带余除法即可。

元素 $c\in A$ 叫做 $f\in A[X]$ 的 $k$ 重根，若 $(x-c)^k\mid f,(x-c)^{k+1}\not\mid f$。

设 $A$ 是整环，$f\neq 0\in A[X]$，$c_{1:r}$ 分别是 $f$ 的 $k_{1:r}$ 重根。则：

证明：若此环不是域，引入分式域，利用唯一因子分解性，包含后面那个 $\prod$，然后容易说明 $g(X)\in A[X]$。

并且此时有：若 $f,g\in A[X]$ 是两个次数 $\le n$ 的多项式，如果它们在 $A$ 中有 $n+1$ 个不同元素取值相同，则 $f=g$。这是前面说明的。

多项式函数和插值

我们已经知道多项式 $f\in A[X]$ 对应一个函数

这样函数的集合构成环 $A_{pol}$，叫做多项式函数环，是点加和点乘为运算的全部 $A^A$ 函数环的一个子环。

我们知道，$\mathbb F_2$ 上的多项式 $X^2+X$ 对应零函数（尽管不是零多项式）。一般地，若 $f(X)=(X^P-X)g(X)\in \mathbb F_p(X),p\in \mathcal P$，$\tilde f$ 是零函数，由费马小定理。那么任意多项式可以通过模 $(X^P-X)$ 来得到 $\deg \le p-1$ 的多项式，函数意义等价。那么 $\varphi(f)=f\bmod (X^P-X)$ 就是一个 $\mathbb F_P[X]$ 到 $\mathbb {F_p}_{pol}$ 的环同态。

而如果这不是有限域而是无限元素的整环，则多项式环 $A[X]$ 到 $A_{pol}$ 的映射 $f\to\tilde f$ 是一个环同构，这是显然的。

我们已经知道在整环上 $n+1$ 个点唯一确定一个 $\deg \le n$ 的多项式（如果可能）。而在域上，下面的拉格朗日插值公式告诉我们此问题一定有（唯一）解。

设 $P$ 是域，希望找到 $\deg\le n$ 的多项式 $f\in P[X]$，使得 $\forall i\in \Z\cap [0,n],f(c_i)=b_i$。

这个公式给出了解。同时，显然可以利用这个公式做到 $O(n^2)$ 求出原多项式（不只是点值）。

P4781

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353,maxn=2005;
int qp(int a,int b){
	if(b==0)return 1;
	int T=qp(a,b>>1);T=T*T%mod;
	if(b&1)return T*a%mod;
	return T;
}
int b[maxn],c[maxn],n,k;
signed main(){
	cin>>n>>k;
	n--;
	for(int i=0;i<=n;i++)cin>>c[i]>>b[i];
	int res=0;
	for(int i=0;i<=n;i++){
		int cur=b[i],s=1;
		for(int j=0;j<=n;j++){
			if(i==j)continue;
			cur=cur*(k-c[j]+mod)%mod;
            s=s*(c[i]-c[j]+mod)%mod;
		}
		(res+=cur*qp(s,mod-2))%=mod;
	}
	cout<<res<<endl;
	return 0;
} 

最后指出，每一个既约分式 $f/g\in P(X)$ 和含有无限多元素的 $P$ 的扩域 $F$ 中，$f/g$ 和 $\widetilde{f/g}$ 是一一对应的。

微分和对称函数

下面设 $P$ 是域。

定义

由于多项式所在的任意环上难以定义微分（就像我们在数学分析做的那样），所以直接根据 $\R$ 上 $\dfrac{d(x^n)}{dx}=nx^{n-1}$ 定义多项式微分：

容易验证：

直接推出

设任意映射 $D:R\to R$ 满足：

称 $D$ 为导子。

设 $R=P[X]$：

归纳可以证明：

那么多项式环的导子由 $DX$ 唯一确定。微分算子是 $DX=1$ 的导子。

如果 $char P=0$，那么 $\deg f'=\deg f-1$。

重因式

用 $(X-c)^2$ 对 $f\in P[X]$ 做带余除法，其中 $c\in F\supset P$。

所以，$c\in F$ 是 $f$ 的重根，当且仅当 $f(c)=f'(c)=0$。

下面设 $char P=0$。

设 $p(X)$ 是 $f\in P[X]$ 的 $k$ 重既约因式（$k,\deg p(X\ge 1$），则 $p(X)$ 是 $f'$ 的 $k-1$ 重因式。

证明：设 $f(X)=p(X)^kg(X),\gcd(p(X),g(X))=1$。

则

只需证明 $p(X)\not\mid kp'(X)g(X)$。而由于多项式环是欧氏环，$\gcd(p(X),g(X))=1$，那么

而 $\deg kp'(X)<\deg p(X)$，证毕。

设

其中 $p_i(X)$ 是 $k_i$ 重既约因式。

那么

证明：根据上面的定理，

其中 $\gcd(u(X),p_i(X))=1$。显然（根据整除性判别法）。

韦达定理和对称函数

设 $n$ 次首一多项式 $f\in P[X]$ 在 $F\supset P$ 中有 $n$ 个根 $c_{1:n}$。

不难发现

写成

令两者相等，得到：

这就是韦达定理。它还引出了对称多项式和初等对称函数，因为这个式子在 $c$ 置换作用下不变。

下面定义了 $\pi\in S_n$ 作用在 $\tilde f(x_{1:n})$ 的结果：

如果 $\forall \pi\in S_n,\widetilde{\pi\circ f}=\tilde f$，称 $f$ 是对称的。

定义 初等对称函数 $s_k(c_{1:n})=(-1)^ka_k$，即：

以及相似的初等对称多项式。不难证明，全体初等对称多项式构成环。

据此，可以证明威尔逊定理：

对于 $\mathbb F_p,p\in \mathcal P$ 上的多项式

当 $p>2$ 时，根据韦达定理：

即 $(p-1)!\equiv -1\pmod p$。这是威尔逊定理。不难证明其逆定理成立。

对称多项式基本定理

定义多项式 $g(s_{1:n})$ 的权 $w(g)$ 是其所有单项式

的权的最大值。

对称多项式基本定理：

设 $f\in A[X_{1:n}]$ 是整环 $A$ 上全次数为 $m$ 的对称多项式，那么存在唯一权为 $m$ 的多项式 $g\in A[s_{1:n}]$，使得 $f=g$，且 $g$ 的系数是 $f$ 在 $\Z$ 的线性组合。

证明：

首先不妨认为 $f$ 是齐次的：把多项式拆分成齐次的方法是唯一的。

把 $f$ 的单项式按 $X_1$ 到 $X_n$ 的指数从大到小字典序排序，设第一个单项式是 $f$ 的首项，记作 $FT(f)$。

引理 1：若 $h=h_1h_2\dots h_r$，$FT(h)=FT(h_1)FT(h_2)\dots FT(h_r)$。

从前到后归纳即可。

称单项式是单调的，若其 $X_1$ 到 $X_n$ 指数不降。

引理 2：对称多项式 $f$ 的首项是单调的。不难发现。

下面开始证明原命题：

设 $u=aX_1^{i_1}X_2^{i_2}\dots X_n^{i_n}=FT(f)$。

考察对称多项式：

而 $w(as_1^{i_1-i_2}s_{2}^{i_2-i_3}\dots s_n^{i_n})=\deg f$，$FT(as_1^{i_1-i_2}s_{2}^{i_2-i_3}\dots s_n^{i_n})=u$。

这样，$FT(f)>FT(f_{(1)})$。而 $f_{(1)}$ 的系数形如 $c-qa$，其中 $c,a$ 是 $f$ 的系数。

这样的过程不能无限进行（递降），证明 $g$ 存在性。也说明了且 $g$ 的系数是 $f$ 在 $\Z$ 的线性组合。

下面证明唯一性。

不难发现，$g(s_{1:n})$ 的所有不同单项式的首项是不同的。因此若 $g(s_{1:n})=0$，其系数全为 $0$。

证毕。

这也意味着 $s_{1:n}$ 是代数无关的，所以环 $A[s_{1:n}]$ 和 $A[X_{1:n}]$ 同构。

设 $P$ 是域，$f(X)=X^n+a_1X^{n-1}+\dots +a_n\in P[X]$，在 $F\supset P$ 上有 $n$ 个根 $c_{1:n}$。设 $h(X_{1:n})\in P[X_{1:n}]$，是对称多项式。则 $h(c_{1:n})\in P$。

证明：

而 $s_k(c_{1:n})=(-1)^k a_k$。故 $g(s_{1:n})\in P[X_{1:n}]$，$h(c_{1:n})\in P$。

待定系数法和牛顿公式

我们希望得到一个对称多项式分解出初等对称多项式的方法。

设整环 $A=\Z$ 或 $\R$，$v$ 是单项式，$S(v)$ 是 $v$ 经过变元的置换得到的不同单项式的和。例如：$S(X_{1:k})=s_k$。

以下默认 $S(v)$ 中的 $v$ 是单调的（不影响答案）。显然，对于任何 $A$ 上的对称多项式，

通常这样的表达方式一眼就可以看出来。

每个单调的单项式 $v=\displaystyle\prod_j X_j^{i_j}$ 对应一个初等对称多项式：

取所有单调的 $<v$ （字典序意义下）的单项式集合 $M_v$。我们已经知道：

其中 $n_w\in \Z$。将若干整数代入 $X$，可以解出 $n_w$。这是待定系数法。

设幂和 ${\bf p}_k(X_{1:n})=S(X_1^k)=\sum X_i^k$。

牛顿公式：

若 $1\le k\le n$：

若 $k>n$：

现在来挑战 P4500 吧！

证明：首先不难证明，对于 $k\ge n$，有：

对其求和得到 $k\ge n$ 时的公式。考虑 $k<n$：

进而考察齐次对称多项式 $f_{k,n}$：

对 $n-k$ 归纳。

依靠归纳假设，不难证明 $f_{k,n}(X_1,X_2,\dots ,X_{n-1},0)=0$。

所以 $X_n\mid f_{k,n}$。所以 $s_n\mid f_{k,n}$。而 $\deg f_{k,n}<\deg s_n$，故 $f_{k,n}=0$。

判别式和结式

考察 $P[X_{1:n}]$ 中的对称多项式

$Dis$ 是根据对称多项式基本定理搞出来的多项式，称为判别式。

显然，判别式能够判别是否有重数。

发现这个形式是范德蒙德矩阵的行列式：

考虑 $\det AB=\det A\det B$，而 $\det A^T=\det A$，所以 $Dis(s_{1:n})=\Delta_n\Delta^T_n$。（就是把上面的矩阵转置）

乘起来得到：

一个多项式 $f=X^n+a_1X^{n-1}+\dots +a_n\in P[X]$ 的判别式 $D(f)\in P$ 是对其根的判别式，即 $s_k=(-1)^ka_k$。

不难发现 $D(f)=0\iff f(X)=0$ 有重根。

设

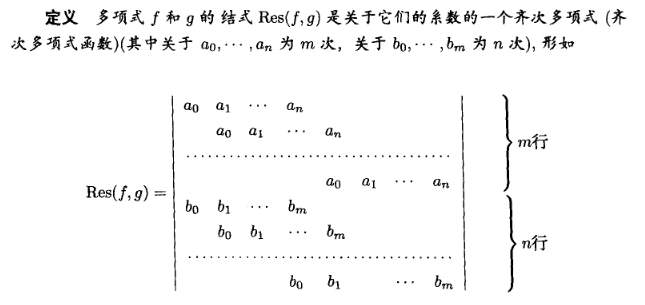
不会打矩阵，，，

不难发现 $Res(g,f)=(-1)^{mn}Res(f,g)$。

证明：

引理：

证明：

设 $h=\gcd (f,g),\deg h>0$。则$f=hf_1,g=-hg_1$ 满足条件。

若 $\gcd(f,g)=1$，根据 $P[X]$ 分解唯一，$fg_1=-gf_1\Rightarrow f\mid f_1,g\mid g_1$。此时只能 $a_0=b_0=0$。

回到原命题证明。

考虑

考虑 $fg_1+gf_1$ 多项式的系数：可以列出方程：

显然全 $0$ 是一个解。而存在其他解的充要条件是系数矩阵行列式非零。注意到系数矩阵的转置是 $Res(f,g)$。证毕。

设 $f,g\in P[X]$ 可以在 $P[X]$ 中分解成线性因式。

则：

没看懂证明在说什么。

不难发现。

域 $\C$ 的代数封闭性

域 $P$ 是代数封闭的，如果 $P[X]$ 的每个多项式都可以分解为线性因式的乘积。

如果任意多项式在 $P$ 上至少有一个根，那么 $P$ 是代数封闭的，根据归纳法。

代数封闭的逸车。

定理（代数基本定理）：$\C$ 是代数封闭的。

首先，我们必须引入两个数学分析的结论：

每个复多项式

是在平面 $\C$ 任意一点都连续的函数。

每个在紧集 $K\subset R^2$ 上的连续函数 $f:K\to \R$ 都在 $K$ 上达到自己的最小值（我们用的的是 $|z|\le r$ 的圆）。

带几何直观的证明

引理 1：$\exists r\in \R^+\text{ s.t. }|f(z)|>|f(0)|,\forall |z|>r,z\in \C$。

对于 $z\neq 0$，$|f(z)|=|z|^n|a_0+g(z^{-1})|$，其中 $g\in C[u]$。因为 $g$ 在 $0$ 连续，$\exists \delta>0,|g(u)|\le \dfrac{|a_0|}2,\forall |u|< \delta$。那么：

$\forall |z|>\delta^{-1}$。

选取 $r>\delta^{-1}$ 且 $|a_0|r^n>2|a_n|$ 即可。

引理 2：设 $k\in \N^+,h\in \C[z],h(0)\neq 0$。那么 $\forall a\in \C^*$，$\exists b\in \C$，使得

$\exists \delta>0\in \R,|h(z)-h(0)|<\dfrac{|h(0)|}{2},\forall |z|<\delta$。那么 $\forall |z|<\delta$：

取 $b\in\C$ 使得 $h(0)b^k=-ta,t\in (0,1)$。

那么

令 $t<|h(0)a^{-1}|\delta^k$，这样保证了 $|b|<\delta$。

引理 3（达朗贝尔-阿尔冈引理）：设 $f(z)$ 是 $\C$ 上的正次数多项式。那么 $\forall f(c)\neq 0,c\in \C,\exists c'\in \C$，使

证明：考虑把 $f(c+z)$ 按 $z$ 展开：

其中 $\deg h(z)\le n-k$。

把 $a=f(c)\neq 0$ 代入引理 2 即证。

引理 4（关于最小值的柯西引理）：$\forall f\in \C[z],\exists z_0\in \C,|f(z_0)|=\inf_{z\in C}|f(z)|$。

根据所给出的数学分析的命题，连续函数 $|f(z)|$ 在圆 $D_r=\{z\in\C\mid |z|\le r\}$ 取到最小值。即 $\exists z_0\in D_r,|f(z_0)|=\inf_{z\in D_r}|f(z)|$。而 $|f(z_0)|\le |f(0)|$，根据引理 $1$，$r$ 是可以被选取使得 $|f(0)|\le \inf_{z\in \C-D_r}|f(z)|$。所以 $|f(z_0)|=\inf_{z\in C}|f(z)|$。

根据引理 $4$：存在 $z_0\in\C$ 使得 $z\in \C$ 有 $|f(z_0)|\le |f(z)|$。若 $|f(z_0)|\neq 0$，$\exists z_0'\in \C,|f(z_0')|<|f(z_0)|$，矛盾。故 $f(z_0)=0$，找到了一个根 $z_0$。证毕。

为什么说这个证明带几何直观呢？因为引理 $3$ 是说，如果在曲面 $w=f(z)$ 上存在一个严格在 $w=0$ 上方的点，必然存在另一个点和 $w=0$ 更近。

关于最高次项模的引理

设 $f(z)\in \C[z]=\sum_ia_iz^{n-i}$。令 $A=\max(|a_i|),r=\dfrac{A}{|a_0|}+1$。

当 $z>r$ 时有：

证明：则 $|a_0|\ge \dfrac A{|z|-1}$。不难放缩得到。

推论：实系数的奇次数多项式必有实根。不难发现。

还有个承认存在分裂域基础上的神秘代数证明，先不管了。

实系数多项式

设 $f\in \R[X]$，对于任意复根 $f(c)=0\iff \overline f(\overline c)=0\iff f(\overline c)=0$。所以 $(x-c),(x-\overline c)\mid f$。而若 $c\in \R$，$(x-c)$ 是 $f$ 的一次既约因式。否则，$(x-c)(x-\overline c)$ 是二次既约因式。由 $\C$ 的代数封闭性知道，$f$ 唯一地分解为若干一次因式和判别式小于零的二次因式的乘积。

隔根与斯图姆组

定义一个实数序列 $S=\{c_i\}_{i=1}^m$ 的变号数为

如果有 $0$，先去掉 $0$。

下面假设多项式无重根。

定义非零实数多项式的有限序列

叫做 $f(x)$ 在闭区间 $[a,b]$ 上的斯图姆组，如果：

显然相邻的多项式没有共同根。

记

斯图姆定理：次数 $n\ge 1$ 的实多项式 $f(x)$ 在开区间 $(a,b)$ 上的根数目等于 $V_a-V_b$，这两个对应一个斯图姆组。

证明：

设这些斯图姆组里面的多项式的实根撒在 $[a,b]$ 上，把他分成了若干个子开区间 $(a_j,a_{j+1})$，满足 $a=a_0<a_1<\dots <a_m=b$。在这些子开区间中任何多项式 $f_i$ 都没有根。

取 $c\in (a_0,a_1)$。根据柯西中值定理，$f_i(a_0)f_i(c)\ge 0,\forall i$。若 $f_k(a_0)=0$，必有 $\forall k\in [1,s-1]\cap\Z,f_{k-1}(a_0)f_{k+1}(a_0)<0$。而相邻的多项式没有共同根，$f_{k-1}(a_0)f_{k-1}(c)>0,f_{k+1}(a_0)f_{k+1}(c)>0$。所以 $f_{k-1}(c)f_{k+1}(c)<0$。这表明（由于变号数去 $0$）$V_c=V_{a_0}$。

类似的讨论适用于同样的情况：$c\in (a_{m-1},a_m)\Rightarrow V_c=V_{a_m}$。

设 $c\in (a_{j-1},a_j),c'\in (a_j,a_{j+1})$，那么 $V_c=V_{c'}$？

不正确！前面由于有 $f(a)\neq 0$ 的限制得到 $V_c=V_{a_0}(c\in (a_0,a_1))$。当 $f(a_j)=0$ 时，出现不一致。由于性质 $4$，得到 $V_c-V_{c'}=1$。否则， $V_c=V_{c'}$。

所以，如此实多项式 $f(x)$ 在开区间 $(a,b)$ 上的根数目等于 $V_a-V_b$。

接下来的问题：如何对多项式 $f(x)$ 构造斯图姆组呢？

取 $f_0(x)=f(x),f_1(x)=f'(x)$。

根据定义，$f_s(x)=\gcd(f,f')$ 是非零常数，因为 $f$ 没有重根。如果我们无法确定这一点，所有项除去 $f_s(x)$ 即可（$\gcd(f,f')$ 即是重根相乘）。

上述构造出了一组斯图姆组。

证明：逐条验证即可。

接下来的内容是代数学引论（第 $3$ 卷）的。仅会选取一部分内容。

群论的构造

比较 OI 相关的部分。（？）

陪集

设同态 $f:G\to G'$，则 $\ker f$ 总是 $G$ 的子群，且不难验证有：

它引出了正规子群的定义：群 $G$ 的一个子群 $K$ 称为正规的，当且仅当：

同态核总是正规的。

而考虑这样的集合 $a\ker f$：不难验证，这等于 $\{x\in G\mid f(x)=f(a)\}$。这表明，形如 $a\ker f$ 这样的集构成了 $G$ 的分割。这引出了陪集的定义。

设 $H\subset G$，子群 $gH, g\in H$ 称为 $H$ 的左陪集。$g$ 称为该陪集的代表元。

定理：$H$ 的两个左陪集要么相等要么没有公共元。因此 $H$ 的左陪集构成了对 $G$ 的分割，也给出了 $G$ 中的一个等价关系。

证明：

设 $a\in g_1H\cap g_2 H,a=g_1h_1=g_2h_2$，那么 $g_2=g_1h_1h_2^{-1}$，$g_2x=g_1 (h_1 h_2^{-1}x)$，那么 $g_2 H\subset g_1 H$。从而 $g_2H=g_1 H$。

同一子群的左右陪集的分割集合大小相等。不难验证，取左陪集分割集合的代表元集合 $\{e,x,y,z\dots\}$，右陪集的就是 $\{e,x^{-1},y^{-1},z^{-1},\dots\}$。

记 $G/H$ 是分割集合。记 ，称为 $H$ 在 $G$ 中的指数。$|G/H|=(G:H)$。不难验证，对于左陪集 $gH$，$f:H\to gH,f(x)=gx$ 是双射，因此 $|gH|=|H|$。那么有公式：

这里 $(G:e)$ 表示对单位子群的陪集个数，也就是这个群的大小。

立即得到拉格朗日定理：

有限群的阶被其子群的阶整除。

推论：$p,p\in \mathcal P$ 阶群 $G$ 同构意义下唯一。

我们已经知道相同阶循环群同构。只需证明 $p$ 阶群是循环群。考察任意一个非单位元生成的循环子群 $\lang x\rang$，其阶 $\#\langle x\rangle>1,\#\lang x\rang| p$，故 $\#\lang x\rang=p$，$\lang x\rang=G$。而 $\lang x\rang$ 是循环群，故 $G$ 也是。

群作用、Burnside 引理

设 $G$ 是群，$\Omega$ 是一个集合。考虑 $G$ 在 $\Omega$ 上的作用，可以先考虑同态 $\Phi:G\to S(\Omega)$。记 $g\in G$ 对应的变换是 $\Phi_g:\Omega\to\Omega$，那么有 $\Phi_{gh}=\Phi g\circ \Phi_h$。不妨把这样的 $\Phi_g(x)$ 记为 $gx$。那么：

此时说是 $G$ 作用在 $\Omega$ 上。

若 $\ker \Phi=\{e\}$，那么称为忠实的作用。

我们发现，$\Omega$ 内两个元素具有这样的等价关系：$x_1,x_2$ 等价，如果 $\exists g\in G,x_1=gx_2$。这样的等价关系的诸性质不难验证。因此，群作用把集合分为了若干等价类，称为轨道。

记 $x_0\in \Omega$ 的轨道是 $G(x_0)=\{gx_0\mid g\in G\}$。

定义 $x_0\in \Omega$ 的稳定子群（稳定子）

不难根据同态性质验证其是子群。

考虑

所以稳定子群的左陪集 $gSt(x_0)$ 和轨道 $G(x_0)$ 的点一一对应。

所以

使用拉格朗日定理知道，任何轨道长是 $|G|$ 的因子。

利用前面的公式，进一步得到所谓轨道-稳定子定理：

设 $x_0'\in G(x_0),x_0'=gx_0$。那么：

那么 $g^{-1}St(x_0')gx_0=x_0$，即：

而 $|St(x_0)|=|St(x_0')|$，那么：

称两个子群 $H,H'$ 共轭，若 $\exists g\in G,gHg^{-1}=H'$。

那么有：

定理：

若 $x_0,x_0'$ 位于同一轨道，那么其稳定子群共轭。

若 $G$ 是有限群，

是 $\Omega$ 以 $x_i$ 为代表元的轨道的分割，那么：

老实说我不觉得这两个东西有关联

在上式的基础上，我们可以证明 Burnside 引理：

设 $\Omega/G$ 是轨道集合，$N(g),g\in G$ 是 $g$ 作用下的不动点个数，有：

证明：

这一部分的讨论中，我们把 $\Omega$ 的元素当成 $\{1,2,\dots n\}$。

如果群 $G$ 在 $\Omega$ 上的作用满足：$\forall i,j\in [1,n],\exists g,g(i)=j$，那么称 $G$ 在 $\Omega$ 上是可迁作用。同样，在 $\Omega^k$ 上满足条件的称为 $k-$ 可迁作用。

记 $g_i(i)=1$（$G$ 不一定只有 $g_i$），则不难验证：$St(i)=g_iSt(1)g_i^{-1}$。那么 $|St(i)|=|St(j)|$。根据前面的定理知道， $|G|=n|St(i)|,\forall i$。

同时不难验证，$g_i$ 可以选为 $St(j)$ 左陪集的代表元：

定理：

如果 $G$ 在 $\Omega$ 上是可迁群：

不难证明。

如果 $G$ 在 $\Omega$ 上是 $2-$ 可迁群：

证明：

则 $St(1)$ 在 $\Omega'=\Omega-\{1\}$ 上是可迁群。那么

这里 $N'(g)$ 指在 $\Omega'$ 上的。

而 $\forall g\in St(1),N(g)=N'(g)+1$，那么：

显然这对其他 $x\in \Omega$ 适用。对其求和，得到：

证毕。

群同态、同构定理

下面，定义两个集合的积 $AB=\{ab\mid a\in A,b\in B\}$。

$H$ 是 $G$ 的正规子群，记为 $H\triangleleft G$。

此时，注意到曾经提到过的根据陪集是否相等划分的等价类具有更好的性质：若 $aH=bH,cH=dH$，则不难验证 $acH=bdH$。

那么：这样定义的乘法 $(aH)\cdot (bH)=abH$ 使 $G/H$ 成为一个群。称为 $G$ 模 $H$ 的商群。

若 $f$ 是同态，我们已经知道，$\ker f\triangleleft G$。此时的商群具有非常浩的性质。具体地：

群同态基本定理：

（1）对于同态 $\varphi :G\to H$，设 $K=\ker \varphi$，则 $K\triangleleft G$，且 $G/K\cong Im \varphi$。

（2）同样地，对于 $K\triangleleft G$，则 $H=G/K,\exists \pi :G\to H,\ker \pi =K$。

先证明 （1）。

构造

不难验证这是同态。而显然 $Im \overline \varphi=Im\varphi$。只需证明此同态单。

证毕。

对于 （2），构造 $\pi(g)=gK$ 即可。

群同构第一定理：

设群 $H,K\subset G,K\triangleleft G$，则：

证明：

$(1)$：

由于 $gK=Kg,\forall g\in G$，显然有 $HK=KH$。

只需证明 $HK$ 是子群。$(HK)^2=HKHK=H(KH)K=HHKK=HK$，而 $(hk)^{-1}=h^{-1}(hkh^{-1})^{-1}\in h^{-1}K\subset HK$。

$(2)$：显然 $K\triangleleft HK$，所以存在商群 $HK/K$。

根据群同态基本定理，考虑满同态 $f:G\to G/K$。其在 $H$ 中的 $f_0=f\mid _H$ 显然也是同态。

考虑 $x\in \ker f_0\iff xK=K\iff x\in K$。故 $\ker f_0=(H\cap K)\triangleleft H$。

$(3)$：

显然 $Im f_0=HK/K$，根据群同态基本定理，$H/(H\cap K)\cong HK/K$。

群同构第二定理（对应定理）：

设 $K\triangleleft G,K\subset H\subset G$。记 $\Omega(S)=\{S'\mid S'\subset S\},\Omega(S,K)=\{S'\mid K\subset S'\subset S\}$，$\overline S=S/K$.

那么：

（2）记 $\pi(S)=\overline S$，则 $\pi:\Omega(G,K)\to \Omega(\overline G)$ 是双射。

（3）$H\triangleleft G\iff \overline H\triangleleft\overline G$，如果成立，则：

（1）显然。

（2）

先验证其单射。考虑 $H_1,H_2\in \Omega(G,K),H_1/K=H_2/K$。

对于任意 $h_1\in H_1$，$\exists h_2\in H_2,h_1K=h_2K$。则 $h_1=h_2k,h_1\in H_2$。那么 $H_1=H_2$。

再验证其满射。设 $K\subset S,\overline S\in \Omega(\overline G),S=\{g\in G\mid gK\in \overline S\}$。那么：

而

所以 $S\subset G$，$\overline S=S/K$。故其满射。

（3）

先证 $H\triangleleft G\Rightarrow \overline H\triangleleft \overline G$。 $gKhKg^{-1}K=ghg^{-1}K=h'K\in \overline H$。

再证 $H\triangleleft G\Leftarrow \overline H\triangleleft \overline G$。 $ghg^{-1}K=gKhKg^{-1}K=(gK)\cdot (hK)\cdot (gK)^{-1}=h'K$。

考虑自然满同态

$\sigma$ 显然是同态。

所以根据群同态基本定理：

此时我们迫切地需要一个例子。我们举循环群的例子。设 $n=dm,n\in \N,d>1$。显然有 $n\Z\subset d\Z$。设 $H=d\Z,G=\Z,K=n\Z$。

考虑 $f:\Z\to d\Z/n\Z,f(x)=dx+n\Z$ 显然是满同态，核为 $m\Z$。由群同态基本定理，

根据群同构第二定理：

即

由拉格朗日定理：所有循环群及其子群必同构于 $H,K$。那么我们得到循环群的子群和商群都是循环群。

当然这只是一个例子，这个结果可以不用同态定理得出。