卡方检验随笔
一 什么是卡方检验
考虑这样一个场景：有一枚硬币，我们希望知道，这枚硬币是否是均匀的。于是我们抛了100次，查看正面和反面的次数，根据这个结果来判断这个硬币是否为均匀的。
1）有50次正面，50次反面，那么我们觉得基本上这个硬币是均匀的；
2）有55次正面，45次反面，我们也觉得硬币差不多是均匀的；
3）有80次正面，20次反面，那么我们觉得这个硬币似乎没有那么均匀；
4）有99次正面，1次反面，那么我们就觉得这个硬币基本不均匀了。
这就是我们面对投掷结果的主观判断。但是这样的结果都是基于经验产生的，是否有一种可以量化的数学方法呢？这就引出了卡方检验。卡方检验就是将上述四句话中标出的经验性判断，量化成具体的数值，让我们的结果有理可循。
-- By Brisk yu 2022-05-19
二 怎么计算卡方值
卡方检验的目的就在于计算一个称为“卡方”的值：X2。通过介个值，我们就可以判断出“硬币是否为均匀的”。那么下面首先看一下，这个值的计算公式：
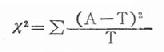
其中A为观测值，T为期望值。在抛掷硬币的例子中，比如有80次正面，20次反面，但是我们期望正反面均为50次，那么此时的X2为：(80-50)2/50 + (20-50)2/50 = 36。具体来说，对于每种情况的值如下：
1）(50-50)2/50 + (50-50)2/50 = 0
2）(55-50)2/50 + (45-50)2/50 = 1.0
3）(80-50)2/50 + (20-50)2/50 = 36.0
4）(99-50)2/50 + (1-50)2/50 = 96.04
显然，从直观上我们已经可以看出来，X2值越小，硬币越可能是均匀的。因为这里我们的期望是正反50次，即硬币是均匀的，因此我们就说：值越小，越符合期望；值越大，越不符合期望。
三 怎么根据卡方值确定结果
还是抛掷硬币的例子，上面的结论只是一个趋势，那么我们究竟如何根据卡方值来确定硬币是否为均匀的呢？
历史上牛逼的科学家发现X2值这玩意服从一个称为卡方分布的东西，那么我们就可以根据卡方分布计算出某个卡方值出现的概率。并且我们提前设定一个阈值，来判断结果是否符合期望（即，硬币是均匀的）。
卡方分布的图像如下：
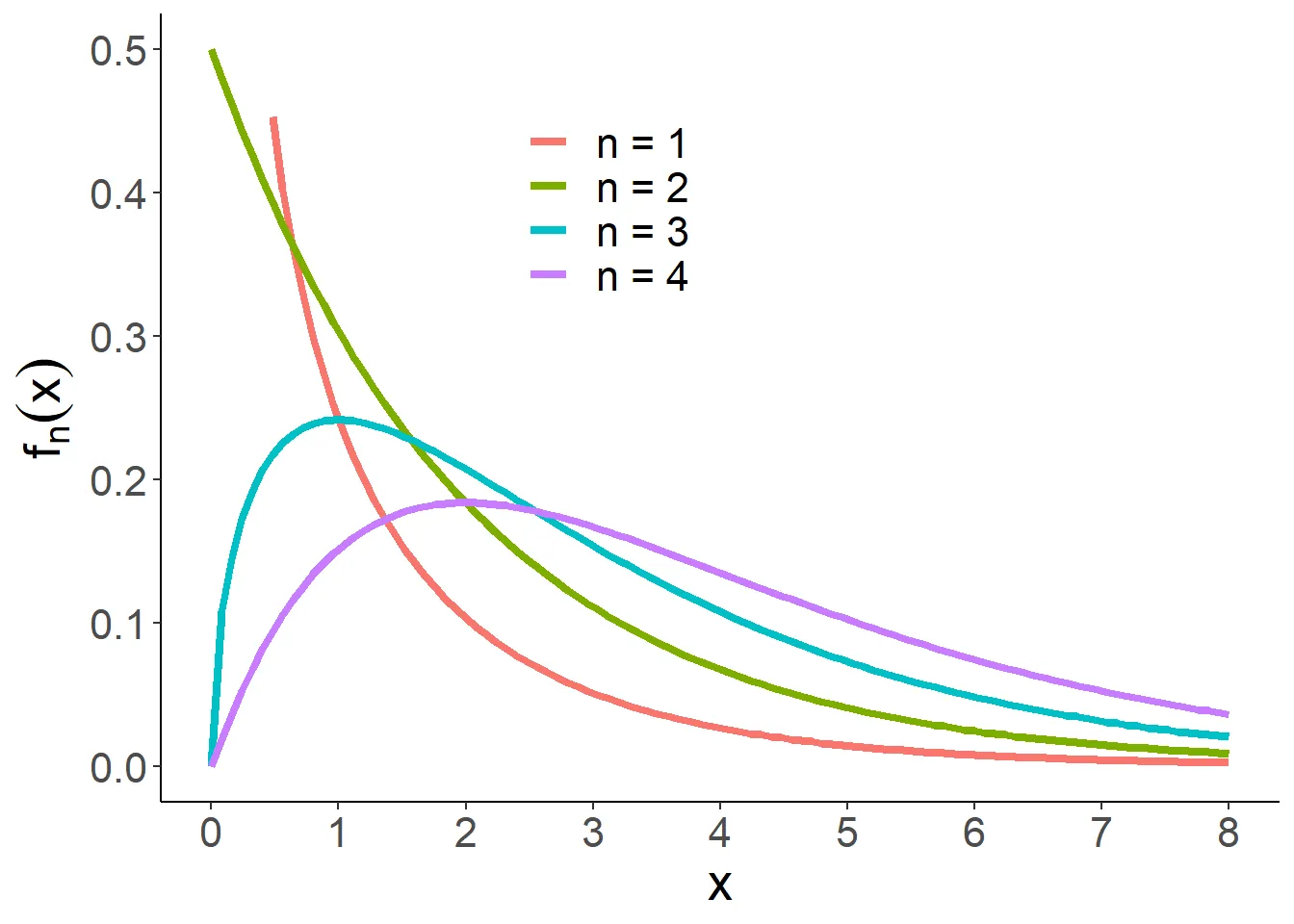
水平座标即为卡方值。可以看出，如果希望计算出这个卡方值出现的概率，则还需要n这个值。n在这里称为自由度，即可以自由确定的变量个数。考虑在抛掷硬币的实验中，假设我们抛掷100次，正面的次数自由确定后，反面的次数显然为 (100-正面次数) ，因此自由度为1。
有了自由度，有了卡方值，我们就可以获取该卡方值出现的概率。这里我们一般使用查表法，下图为自由度为1的卡方分布表：
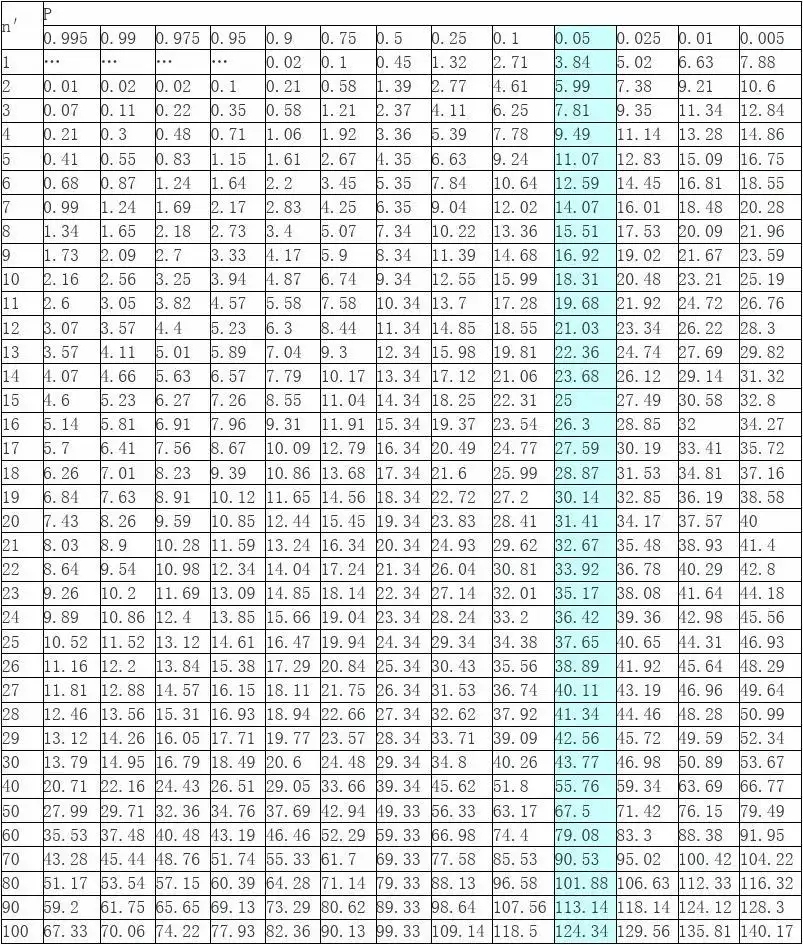
针对一开始的四种情形，结合卡方分布表，我们大致可以得出每种情况出现的概率：
1）卡方值=0<0.02，P>0.9，这种情况出现的概率大于0.9；
2）卡方值=1.0 在0.45和1.32之间，P在0.5和0.25之间，这种情况出现的概率大于0.25小于0.5；
3）卡方值=36.0>7.88，P小于0.005，这种情况出现的概率小于0.005；
4）卡方值=96.04，同上。
因此，我们可以看出，如果我们设定一个阈值，比如0.05，我们就会说：假设硬币是均匀的，置信度为0.05，如果出现1)2)，则在P在置信区间内，接受原假设；如果出现3)4)，则P在置信区间外，拒绝原假设。
四 总结
这里只是举了投掷硬币的例子。其实卡方检验具有广泛的应用场景，比如机器学习特征选择中的相关性检验。当我们计算两个特征是否具有相关性时候，可以先假设两个特征具有相关性，然后再使用卡方检验判断是否接受假设。
