判断正整数各个数位上的数字关系（算法）

问题描述：

示例：

 

解题思路：

1. 首先解决输入的数据和各组数据的上下边界：
   

   // main method
   BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
   String NStr = br.readLine();
   int N = Integer.parseInt( NStr );
   
   int[] aN = new int[ N ];
   int[] bN = new int[ N ];
   // 读取各组数据
   for( int i = 0; i < N; i++ ) {
       String[] data = br.readLine().split(" ");
       aN[i] = Integer.parseInt( data[0] );  // 区间的左边界
       bN[i] = Integer.parseInt( data[1] );  // 区间的右边界
   }

2. 接下来对 [A, B] 区间进行遍历，对该区间内的所有数进行检查（调用 check 函数），如果返回的 score 比现有的 score 大，则更新现有的 score：
   
   

   public static int find( int A, int B ) {
       int score = 0;
   
       for( int n = A; n <= B; n++ ) {
           String nStr = String.valueOf( n );
           int tmpScore = check( nStr );  // 检查 n 字符串是不是 cc number，并且返回它的 score
           if( tmpScore > score )
               score = tmpScore;
       }
       return score;  // 返回的是 A-B 区间内的 CC Number 的最大 Score
   }

3. 核心算法，检查这个数是否为 CC number，若是，则计算并返回它的 score：
   

   public static int check( String nStr ) {
       char cp, cb;  // pre, back
       int score = 0;
       int up1Start = -1, down1Start = -1, down1End = -1;
       int up2Start = -1, down2Start = -1;
       boolean isCCNumber = false;
       for( int j = 0; j < nStr.length() - 1; j++ ) {
           cp = nStr.charAt( j + 1 );
           cb = nStr.charAt( j );  // current char
   
           if( up1Start == -1 ) {
               if( cp > cb) {
                   // start up1
                   up1Start = j;
               }
           }
           else {
               if( down1Start == -1 ) {
                   // on up1
                   if( cp == cb ) {
                       up1Start = -1; // reset up1start
                   }
                   else if( cp < cb ) {
                       // start down1
                       down1Start = j;
                   }  // no need to process case cp > cb again
   
               }
               else {
                   if( down1End == -1 ) {
                       // on down1
                       if (cp >= cb) {
                           down1End = j; // finish down1
                       } // no need to process case cp < cb
                   }
                   else {
                       // check up-down second time
                       if( up2Start == -1 ) {
                           if( cp > cb && cb != '0' ) {
                               // start up2, cb can not be '0'
                               up2Start = j;
                               if( up2Start - down1End != 1 ) {
                                   up1Start = -1;
                                   down1Start = -1;
                                   down1End = -1;
                                   up2Start = -1;
                                   continue;
                               }
                           }
                       }
                       else {
                           if( down2Start == -1 ) {
                               // on up2
                               if( cp == cb ) {
                                   up2Start = -1; // reset up1start
                               }
                               else if( cp < cb ) {
                                   // start down2
                                   down2Start = j;
                                   isCCNumber = true;
                                   break; // no need to know where down2 ends
                               }  // no need to process case cp > cb again
   
                           } 
                           // else {
                           //    if( down2End == -1 ) {
                           //        // on down2
                           //        if (cp >= cb) {
                           //            down2End = j;
                           //        } // no need to process case cp < cb
                           //    }
                           // }
                       }
                   }
               }
           }
       }
       if( isCCNumber ) {
           score = calcScore( nStr );
       }
   
       return score;
   }

    

4. 计算 score 的函数，只需要将该数字对应的字符串上每个字符与 '0' 字符的差值相加即可：
   

   public static int calcScore( String nStr ) {
       char c;
       int score = 0;
       for( int i = 0; i < nStr.length(); i++ ) {
           c = nStr.charAt( i );
           score += ( c - '0' );
       }
       return score;
   }

完整代码：

https://github.com/BriFuture/blog-code-example/blob/master/18-06to09/ccnumber/Main.java

核心步骤算法（check 方法）说明：

对于每个给定的数，要判断它是否为 CC number，有以下步骤：

从左往右（index 从 0 到 length - 1）依次判断相邻位数上的数字大小关系（循环），将当前数位上的数位 numCurr（对应代码中的 nb），下一个数位上的数标记为 numNext（对应代码中的 np）

每次循环从第 1 步开始：

1. 若 up1Start 尚未被标记：
       - 判断 numNext > numCurr，若为 true 说明开始处于第一段 up 区域，将 up1Start 记为当前索引，执行第 2 步；
   若 up1Start 已被标记，执行第 2 步；
   
   
2. 如果 down1Start 尚未被标记，判断 numNext 与 numCurr 的关系：
       - 若 numNext == numCurr，清除 up1Start 的标记，返回第 1 步；
       - 若 numNext < numCurr，将 down1Start 记为当前索引，执行第 3 步；   
   如果 down1Start 已被标记，执行第 3 步；
   
   
3. 如果  down1End 尚未标记判断 numNext 与 numCurr 的关系：
       - 若 numNext >= numCurr，将 down1End 记为当前索引，执行第 4 步；
       - 否则继续执行第 3 步；
   如果  down1End 已被标记，执行第 4 步，
   
   
4. 如果 up2Start 尚未标记，进行判断：
       - 若 numNext > numCurr 并且 numCurr 不为 0（C number 的最高位不能为 0），
         判断当前索引与 down1End 的差值，
            * 若差值不为 1，则需要重置所有标志位，执行第 1步，
            * 否则执行第 5 步；
       - 否则继续执行第 4 步；
   否则执行第 5 步；
5. 如果 down2Start 尚未标记，判断 numNext 与 numCurr 的关系：
       若 numNext == numCurr，清除 up2Start 的标记，返回第 4 步；
       若 numNext < numCurr，将 down2Start 标记为当前索引，标记 isCCNumber 为 true，跳出循环；
       否则继续执行第 5 步;

上述步骤结束后，判断 isCCnumber，若为真的话说明这个数字是 CC number，计算它的 score 并返回，否则返回 0。

 

关于算法的思考，

做题的时候没有仔细思考这个题目，思路比较直接，其实这个位置的解法步骤有点复杂，实际上可以把它当做有限状态机来做：

public enum State { Start, Stage1Up,Stage1Down, StageNext, Stage2Up, /*Stage2Down*/};
public static int checkWithFSM( String nStr ) {
    State currState = State.Start;
    char cp, cb;  // pre, back
    int j = 0;
    while( j < nStr.length() - 1 ) {
        cp = nStr.charAt( j + 1 );  // next char
        cb = nStr.charAt( j );      // current char
        switch ( currState ) {
            case Start:
                if( cp > cb )
                    currState = State.Stage1Up;  // state State1Up
                else
                    currState = State.Start;
                break;
            case Stage1Up:
                if( cp == cb )
                    currState = State.Start;  // reset
                else if( cp < cb )
                    currState = State.Stage1Down; // end of Stage1Up
                // else Stage1Up
                break;
            case Stage1Down:
                if( cp >= cb ) {
                    currState = State.StageNext;  // end of Stage1Down
                }
                // else Stage1Down
                break;
            case StageNext:
                if( cp > cb && cb != '0' )  // maximum number can not be '0'
                    currState = State.Stage2Up;  // start  State2Up
                else
                    currState = State.Start;  // Stage1Down 和 Stage2Up 不相邻，reset
                break;
            case Stage2Up:
                if( cp == cb ) {
                    currState = State.Start; // not on up, reset currState
                }
                else if( cp < cb ) {
//                        currState = State.Stage2Down; // start down
                    return calcScore( nStr );
                }
                // else Stage2Up
                break;
//                case Stage2Down:  // no need to care about Stage2Down state

        }
        j++;
    }

    return 0;
}

换成 FSM 来做之后流程更加清楚了，具体细节也就不再赘述，流程图如下：

 

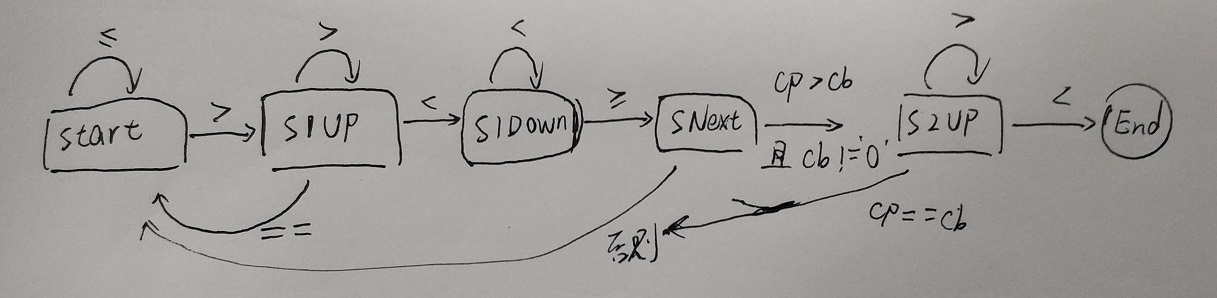
回顾问题：

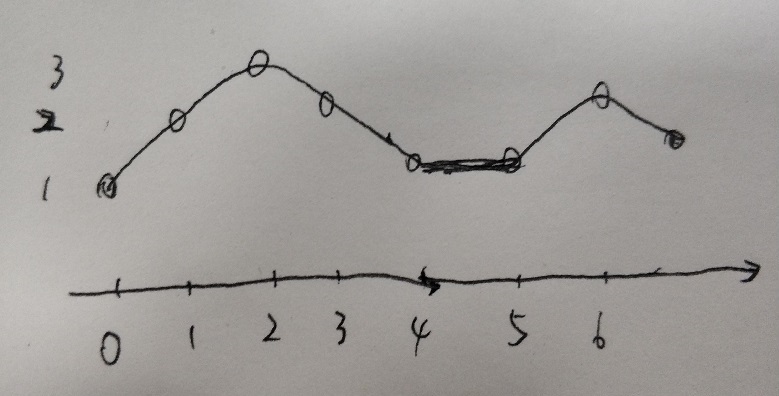
将数字 n 上各个数位当作横坐标（离散取值，范围从 0 到 length - 1），各个数位的数字（0-9）当作纵坐标（离散取值，范围从 0 到 9），可以得到一个离散取点的二维平面图，平面图的走势为先增后减再增再减即可，

需要注意的是第一次下降结束的位置和第二次上升开始的位置重合：

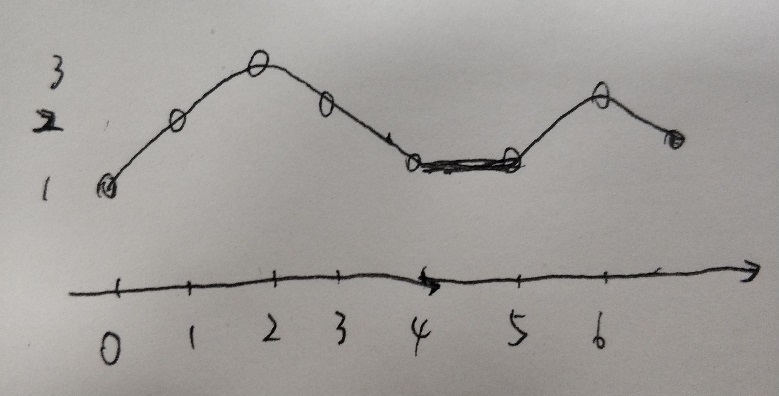
如果连接各个离散的点，up-down，up-down趋势的数据就是符合要求的。