圆与椭圆
一个单位圆的方程是 X2 + Y2 = 1,画在坐标系中:
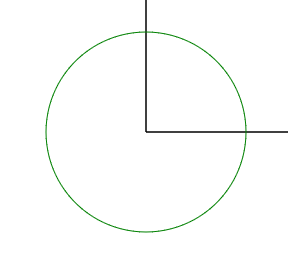
对于圆来说,由于它是高度对称的,旋转属性对它而言意义不大。
在 canvas 画布上绘制一个圆很简单,有两种方法:
1. 使用 html5 中提供的 drawArc API
2. 我们也可以用公式 X2 + Y2 = 1,将 X 从 -1 到 1 中每个微元 dx 对应的纵坐标一个个算出来,然后再将这些点连接起来,只要切割的足够细,那么绘制出来的图形就越接近圆。
只是需要注意的是对于 1 个 x,可能有两个 Y 值与之对应。
3. 我们也可以换一种坐标方程,使用极坐标来表示单位圆,x = cos(θ), y = sin(θ)。θ 在 [0, 2π) 区间内,对于每一个 θ,有唯一的 x, y。
如果不使用 html5 中的 api,绘图的时候选择极坐标方程进行取点会方便很多。
先定义一个方法 drawWithLine:

1 function drawWithLine( v ) { 2 ctx.beginPath(); 3 4 ctx.moveTo( v[0], v[1] ); 5 for( let i = 1; i <= v.numItems; i++ ) { 6 ctx.lineTo( v[ i * 2 ], v[ i * 2 + 1 ] ); 7 } 8 ctx.stroke(); 9 10 ctx.closePath(); 11 }
然后计算出圆上的各点(注意点的顺序)

1 // calcVertex() { 2 let seg = this.seg; 3 let r = this.r; 4 let ox, oy; 5 6 let vertex = []; 7 vertex.itemSize = 2; 8 9 for( let i = 0; i <= seg; i++ ) { 10 ox = Math.cos( 2 * Math.PI * i / seg ) * r; 11 oy = Math.sin( 2 * Math.PI * i / seg ) * r; 12 vertex.push( ox, oy ); 13 } 14 15 vertex.numItems = vertex.length / vertex.itemSize; 16 this.vertex = vertex; 17 return this; 18 // }
将计算出来的点传入 drawWithLine 函数中,就能得到上述图形。
那么如果我们想要绘制椭圆呢,对于一个方程为 X2 + XY + Y2 = 1 的椭圆,我想到的方法是将 Y 表示成 X 的函数,根据 X 的可能取值逐个计算对应的 Y 值,
但是由于 Y 的最高次为 2 次,计算出的 Y 值可能是正值或负值,必须将这两种符号的值分开绘制,否则使用 drawWithLine 方法绘制的椭圆会很奇怪,计算椭圆的顶点:

1 // testOval() { 2 const radius = 10000; 3 const xMax = Math.sqrt( 4 / 3 * radius ); 4 const xMin = - xMax; 5 const seg = 100; 6 const segLength = xMax * 2 / seg; 7 let x, y; 8 let vertex = []; 9 vertex.itemSize = 2; 10 for( let i = 0; i <= seg; i++ ) { 11 x = xMin + segLength * i; 12 y = Math.sqrt( radius - 0.75 * x * x ) - 0.5 * x; 13 vertex.push( x, y ); 14 } 15 for( let i = 0; i <= seg; i++ ) { 16 x = xMax - segLength * i; 17 y = - Math.sqrt( radius - 0.75 * x * x ) - 0.5 * x; 18 vertex.push( x, y ); 19 } 20 vertex.numItems = vertex.length / vertex.itemSize; 21 this._testVertex = vertex; 22 // }
wiki 百科上对椭圆的介绍:

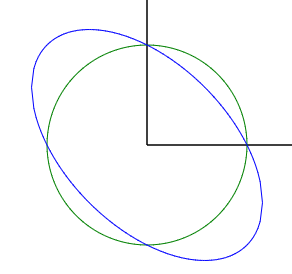
如果我们使用 X2 + XY + Y2 = 1 的系数矩阵 A' = [ 1, 0.5; 0.5; 1 ] 对已经得到的圆(半径为 100 个像素)上各点坐标进行一个坐标变换,得到的图形并没有与前面生成的那个椭圆重合(下方的红色椭圆):
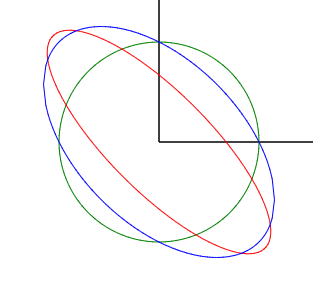
但是如果我们把系数矩阵中的值进行调整的话,比如调整成:[ 1.12, 0.3; 0.3, 1.12 ],(注意到这个位置,第 1 个系数要和第 4 个系数相同,第 2 个系数和第 3 个系数相同)那么经过矩阵变换后得到的椭圆与蓝色的椭圆重合度非常高:
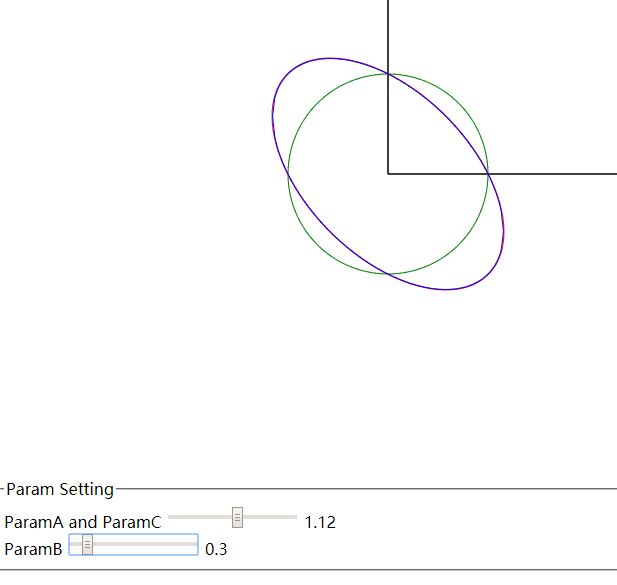
如果只是从圆想得到一个任意平移和旋转的椭圆,可以尝试先将单位圆上的 X 坐标进行矩阵变换,然后对每一个顶点进行矩阵平移和旋转的操作,就可以得到一个任意的椭圆。
如果把 [ 1.12, 0.3; 0.3, 1.12 ] 看成是 [ acos(θ), -bsin(θ); bsin(θ), acos(θ) ],对圆上的坐标进行变换,那么似乎有点道理。
对于其中的具体细节,目前还不了解,以后再继续研究吧。
完整代码:https://github.com/BriFuture/blog-code-example/tree/master/18-06to09/canvas2d/
示例: https://brifuture.github.io/blog-code-example/18-06to09/canvas2d/canvas2d.html
参考
本博客由 BriFuture 原创,并在个人博客(WordPress构建) BriFuture's Blog 上发布。欢迎访问。
欢迎遵照 CC-BY-NC-SA 协议规定转载,请在正文中标注并保留本人信息。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号