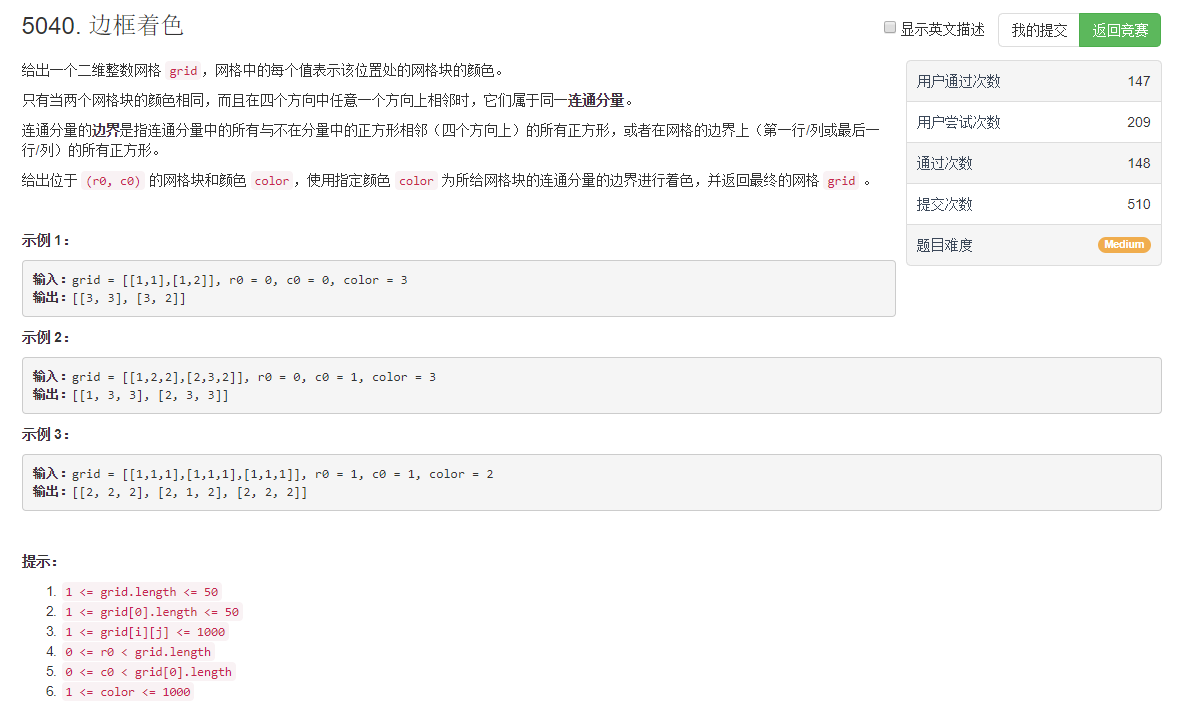
【leetcode 5040. 边框着色】解题报告
方法一:dfs的非递归形式
using ll=long long; const ll MAXN=50LL; unordered_set<ll> vis,mark; vector<vector<int>> colorBorder(vector<vector<int>>& G, int r0, int c0, int color) { queue<ll> Q; Q.push(r0*MAXN+c0); int c=G[r0][c0]; int dx[]={-1,1,0,0},dy[]={0,0,-1,1}; while (!Q.empty()) { int x=Q.front()/MAXN; int y=Q.front()%MAXN; Q.pop(); vis.insert(x*MAXN+y); if (x==0||x==G.size()-1||y==0||y==G[0].size()-1) // 边界方块可变色 mark.insert(x*MAXN+y); else if (G[x-1][y]!=c||G[x+1][y]!=c||G[x][y-1]!=c||G[x][y+1]!=c) // 四个方向中,任意一个方块颜色不同,则可变色 mark.insert(x*MAXN+y); for (int d=0;d<4;d++) // 放入连通分量的所有方块 { int nx=x+dx[d],ny=y+dy[d]; if (0<=nx&&nx<G.size()&&0<=ny&&ny<G[0].size()&&!vis.count(nx*MAXN+ny)&&G[nx][ny]==c) Q.push(nx*MAXN+ny); } } for (auto it:mark) G[it/MAXN][it%MAXN]=color; return G; }
思路:用vis记录访问过的方块,mark标记连通分量中需要修改颜色的方块,并非连通分量中所有的方块都要修改颜色,比如:一个方块如果四周(四个方向邻接的)都是相同颜色,那么只需要修改四周方块的颜色,而自己颜色不变(开始的时候没理解题意,以为只要是连通分量内的方块颜色都需要改变)
方法二: dfs递归形式,只不过把上面的非递归改为递归了
using ll=long long; const ll MAXN=50LL; unordered_set<ll> vis,mark; void dfs(vector<vector<int>>& G, int x, int y, int c) { int dx[]={-1,1,0,0},dy[]={0,0,-1,1}; vis.insert(x*MAXN+y); if (x==0||x==G.size()-1||y==0||y==G[0].size()-1) // 边界方块可变色 mark.insert(x*MAXN+y); else if (G[x-1][y]!=c||G[x+1][y]!=c||G[x][y-1]!=c||G[x][y+1]!=c) // 四个方向中,任意一个方块颜色不同,则可变色 mark.insert(x*MAXN+y); for (int d=0;d<4;d++) // 放入连通分量的所有方块 { int nx=x+dx[d],ny=y+dy[d]; if (0<=nx&&nx<G.size()&&0<=ny&&ny<G[0].size()&&!vis.count(nx*MAXN+ny)&&G[nx][ny]==c) dfs(G,nx,ny,c); } } vector<vector<int>> colorBorder(vector<vector<int>>& G, int r0, int c0, int color) { dfs(G,r0,c0,G[r0][c0]); for (auto it:mark) G[it/MAXN][it%MAXN]=color; return G; }
方法三:dfs递归,但通过修改G中的数据,来记录是否访问过,和是否需要修改颜色,国外的一个大佬写的
From an initial point, perform DFS and flip the cell color to negative to track visited cells.
After DFS is complete for the cell, check if this cell is inside. If so, flip its color back to the positive.
In the end, cells with the negative color are on the border. Change their color to the target color.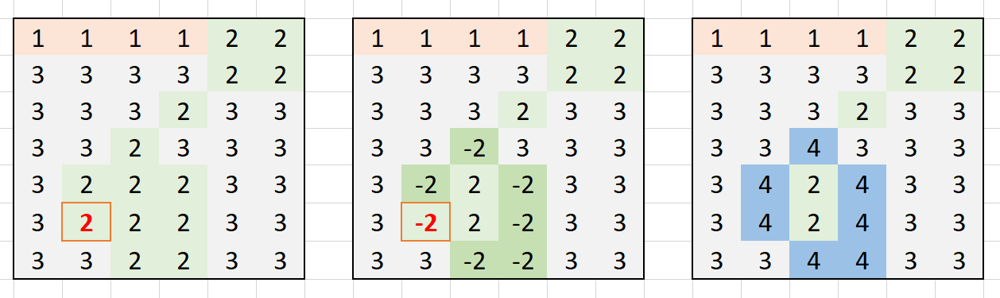
void dfs(vector<vector<int>>& g, int r, int c, int cl) { if (r < 0 || c < 0 || r >= g.size() || c >= g[r].size() || g[r][c] != cl) return; // 剪枝(越界,非着色块) g[r][c] = -cl; // 着色 dfs(g, r - 1, c, cl), dfs(g, r + 1, c, cl), dfs(g, r, c - 1, cl), dfs(g, r, c + 1, cl); if (r > 0 && r < g.size() - 1 && c > 0 && c < g[r].size() - 1 && cl == abs(g[r - 1][c]) && cl == abs(g[r + 1][c]) && cl == abs(g[r][c - 1]) && cl == abs(g[r][c + 1])) // 将原四周同色的块,颜色还原 g[r][c] = cl; } vector<vector<int>> colorBorder(vector<vector<int>>& grid, int r0, int c0, int color) { dfs(grid, r0, c0, grid[r0][c0]); for (auto i = 0; i < grid.size(); ++i) // 根据dfs标记(负数)过的方块进行着色 for (auto j = 0; j < grid[i].size(); ++j) grid[i][j] = grid[i][j] < 0 ? color : grid[i][j]; return grid; }
结论: 无论是递归还是非递归,先标记(标记vis),再遍历




