最小二乘法(Least Squares)

　　最小二乘法(Least Squares)在计算机中是一种用来求参数/最优化的方法（线性/非线性），wikipedia有较为详细的解释：http://en.wikipedia.org/wiki/Least_squares。

　　1）问题陈述：

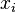　　　　The objective consists of adjusting the parameters of a model function to best fit a data set. A simple data set consists of n points (data pairs) $(x_i,y_i)\!$ , i = 1, ..., n, where $x_i\!$ is an independent variable and $y_i\!$ is a dependent variable whose value is found by observation. 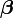The model function has the form $f(x,\beta)$ , where the m adjustable parameters are held in the vector $\boldsymbol \beta$ . The goal is to find the parameter values for the model which "best" fits the data. The least squares method finds its optimum when the sum, S, of squared residuals

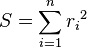
　　　　 $S=\sum_{i=1}^{n}{r_i}^2$

　　　　is a minimum.

　　　　A residual is defined as the difference between the actual value of the dependent variable and the value predicted by the model.

　　　　 $r_i=y_i-f(x_i,\boldsymbol \beta)$ .

　　2）背景：

　　　　Least Squares最早是用在天体运动学中，也就是用在了著名的发现谷神星的故事里——1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。

　　3）如何测量谷神星位置？

　　　　为了理解最小二乘法的作用，我们不妨来模拟下高斯求解谷神星位置的大致过程，可以假设谷神星的运动轨迹符合以下线性方程：

　　　　当然行星运行轨迹的方程不会是这样，但是不妨假设为这样。

　　　　现在我们有三个参数β₀、β₁、β₂，另外根据百科等描述，高斯当时拿到了三组观测值，也就是(y_1,x₁)、(y₂_,x₂)、(y₃_,x₃)，那么现在问题就变成了：利用观测到的三组样本去求解方程里三个参数的最优值，该如何求解？

　　　　高斯想到的是用最小二乘法，最小二乘法的基本公式其实就是残差的平方和，为什么使用这个公式可以看下图：

　　　　可以看出残差平方的图形是一个凹形曲线，极值点就是为0的时候，再看下更多维度的情况：

　　　　现在我们有三组观测值来求解三个参数，且S = 0：

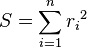
　　　　 $S=\sum_{i=1}^{n}{r_i}^2$

　　　　 $r_i=y_i-f(x_i,\boldsymbol \beta)$

　　　　要求得三个参数β₀、β₁、β₂，很容易想到要找出三个方程组，这样才能求出对应个数的参数，如果我们计算各参数的偏导数，同时设偏导数为0，就能够得到这样的三个方程了。（因为在凹点处，斜率为0，也就是参数最优（在图形底部）的时候）

　　　　三组观测值带入到S中，再对S分别求三个参数的偏导后，则可以得到三个方程组，回顾一下代数：三个线性方程组求三个参数的方法叫做求解线性方程组，这种线性方程组往往都存在closed-form solution即闭合解、封闭解、解析解的，也就是有固定的解的形式，可以直接套用。

　　　　线性方程组求解的方法：http://jpkc.wuse.edu.cn/xxds/xxdsjpkc/Html/tongji/text/ch03/se03/right3_3_1.htm

　　　　也可以转换为矩阵的方式来求解：http://www2.edu-edu.com.cn/lesson_crs78/self/j_4184/soft/ch0201.html　　　　

　　　　求出三个参数后，我们就可以根据时间等未知数来推测神谷星的位置y了。　　　　

　　　　学数学的时候往往不知道这些数学理论到底有什么用，通过这个例子可以看出数学的确是无处不在！

　　　　http://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)

　　4）非线性最小二乘法

　　　　在以上推测谷神星位置的方法中，我们假设了一个线性函数，并通过对各参数偏导的求解，得到对应个数的方程组，将问题转换为线性方程组的求解问题，但是这只适用于线性函数，而实际使用中，例如许多机器学习算法中，我们使用和构造的函数并非线性函数，例如sigmoid函数：

　　　　 $S(t) = \frac{1}{1 + e^{-t}}.$