如何理解递归

如何理解递归

利用递归，我们可以解决很多问题，比如汉诺塔或者八皇后问题。对于一个待求解的问题，他的范围可能会很大，我们无法直接计算出他的答案。当它在小范围，或者某种特殊情况下的答案我们往往是知道的。我们将小范围或特殊情况下的解称为问题边界（我们已经可以从这里解决问题了，不需要再向前探索了）。我们可以抓住问题的特性，从小范围，特殊情况出发，扩大到大范围，一般情况，从而求得问题的解。但是我们如何从小范围扩大到大范围并且得出答案呢?
一个问题可能有很多解决的路径，但其中可能只有一条路径能够到达问题边界，我们需要去尝试所有的路径，去寻找哪条道路可以到达问题边界。

但是找到问题边界我还没有求解问题，但这是我们已经找到了从大问题缩小到问题边界的路径。于是我们可以沿着问题边界反推到大范围，同时进行计算，从而得出问题的解。我们称这个返回的过程为回溯，也就是写程序时的return。

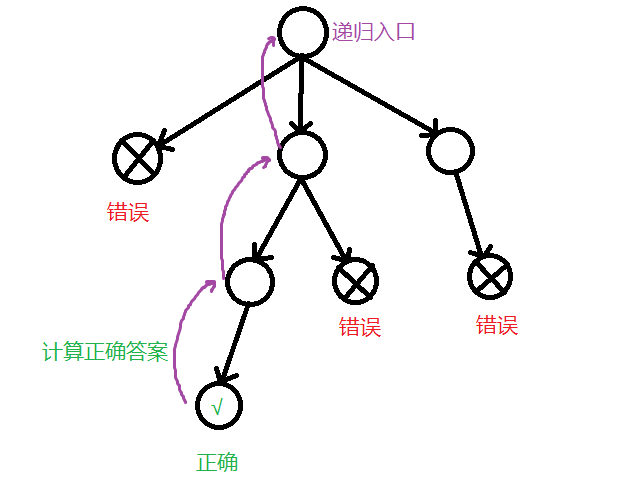
可能又有人要问了，我如何在回溯的时候计算问题的解呢?实际上，从一个较小范围到一个较大范围是有“某种数学上的运算”的，通过将较小范围的答案加以运算，可以得出较大问题的答案，返回后从而进行更大范围的运算。
本文不严谨，仅供小白阅读