3 基本性质（2）解的存在性和唯一性
考虑初值问题：
\[\dot{x}=f(t,x), x(t_0)=x_0 \tag{1}
\]
我们希望解\(x(t)\)存在且唯一。
本节基于Lipschitz条件给出了解存在且唯一的充分条件。
备注：如果\(f(t,x)\)对于\(t\)和\(x\)是连续的，那么解\(x(t)\)将是连续可微的。
我们将假设\(f(t,x)\)对于\(x\)连续，但对于\(t\)仅分段连续。这样允许我们包括\(f(t,x)\)依赖于时变输入，即输入可能随时间经历阶跃变化的情况。
首先是定理3.1的局部存在性和唯一性：
定理3.1是一个局部定理，因为它仅在区间\([t_0,t_0+\delta]\)上保证存在性和唯一性，其中\(\delta\)可能非常小。换句话说，我们对\(\delta\)没有控制；因此，我们无法确保给定时间间隔\([t_o,t_1]\)上的存在性和唯一性。
如何保证其在整个\([t_o,t_1]\)上都有唯一解呢？这个问题将由定理3.2解决：
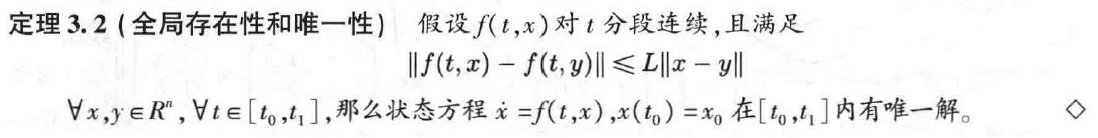
定理3.1中的局部Lipschitz条件，很多物理系统模型都满足。
而定理3.2中的全局Lipschitz性质具有限制性，许多物理系统的模型无法满足这一要求。我们很容易可以构造出没有全局Lipschitz性质，但具有唯一全局解的有意义的例子，这表明定理3.2是保守的。
因此，有必要找到一个全局存在和唯一性定理，要求函数\(f\)仅为局部Lipschitz。这就是定理3.3：
应用定理3.3的诀窍在于，检验每个解都位于紧集的假设是否成立，而不实际求解微分方程。
