3 基本性质(1)Lipschitz条件
Lipschitz条件的定义
对于一个函数\(f(t,x)\),如果对于点\((t_0,x_0)\)的某一邻域内的任意两点\((t,x)\)和\((t,y)\)满足不等式
则称这个不等式是利普希茨条件(Lipschitz condition)。满足该条件的函数称为是关于\(x\)利普希茨的,正常数\(L\)称为利普希茨常数。
根据Lipschitz条件所适用的域,分为局部利普希茨(locally Lipschitz)和全局利普希茨(globally Lipschitz)。
以\(f(x)\)为例:
局部利普希茨
-
定义1:函数\(f(x)\)称为在域(开连通集)\(D\subset R^n\)上是局部利普希茨的,如果\(D\)的每个点都有一个邻域\(D_0\),使得对\(D_0\)中所有点,\(f\)满足式(1),其利普希茨常数为\(L_0\)。
-
定义2:\(f(x)\)在集合W上是利普希茨的,如果它对于\(W\)中的所有点都满足式(1),并且具有相同的利普希茨常数\(L\)。
备注1:域\(D\)上的局部利普希茨函数对于域中的每个点可能有不同的利普希茨常数,而\(D\)上的利普希茨函数对于域中的所有点有相同的利普希茨常数。
备注2:但是,域\(D\)上的局部利普希茨函数在\(D\)的每个紧(闭且有界)子集上是利普希茨的。
全局利普希茨
- 定义3:如果函数\(f(x)\)在\(R^n\)上是利普希茨的,则称其为全局利普希茨的。
类似地,对于\(f(t,x)\),也有如下定义:
-
定义4:\(f(t,x)\)在\([a,b]×D\subset R×R^n\)上是关于\(x\)局部利普希茨的,如果每个点\(x∈D\)都有一个邻域\(D_0\),使\(f\)在\([a,b]×D_0\)上满足式(1),其利普希茨常数为\(L_0\)。
-
定义5:\(f(t,x)\)在\([t_0,∞)×D\)上是关于\(x\)局部利普希茨的,如果对每个紧区间\([a,b]\subset [t_0,∞)\),它在\([a,b]×D\)上是关于\(x\)局部利普希茨的。
-
定义6:\(f(t,x)\)在\([a,b]×W\)上是关于\(x\)利普希茨的,如果它对所有\(t∈[a,b]\)和\(W\)中的所有点都满足式(1),并且具有相同的利普希茨常数\(L\)。
Lipschitz常数的计算(引理3.1)

引理3.1说明了如何使用[∂f/∂x]来计算利普希茨常数。
Lipschitz性质的判断(引理3.2、3.3)
函数的Lipschitz性质比连续性强,但比连续可微性弱。下面两个引理分别给出了局部利普希茨和全局利普希茨的判断:

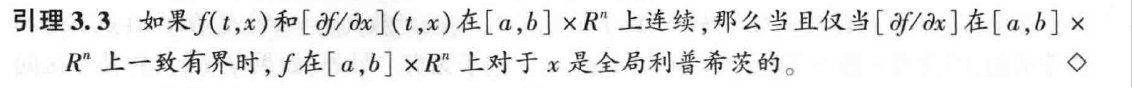



 浙公网安备 33010602011771号
浙公网安备 33010602011771号