快速排序

 

 

 

 

 

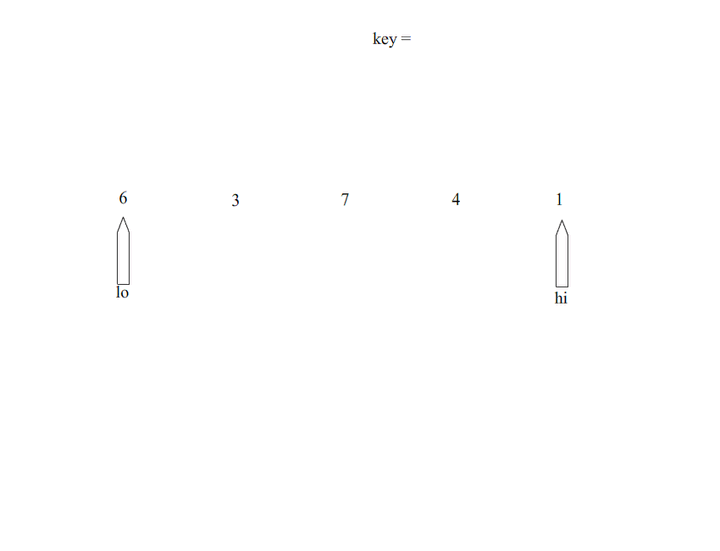
显然，我们从图中可以看出快排运用了二分的思想，首先选择一个基准，定义左右两端指针，先从左到右进行扫描直到，R[hi] < temp,将R[hi]移动至lo所在位置  从右往左进行扫描，直到R[lo] > temp,将R[lo]移动到hi所在位置上，左右端指针在排序过程中从数组的两端往中间进行靠近，直到hi == lo。而快速排序则要进行多次快排过程，直到划分的区间最后长度仅为1.

 

总结下来（转， 自己懒得敲了：

• 选择A中的任意一个元素pivot，该元素作为基准
• 将小于基准的元素移到左边，大于基准的元素移到右边（分区操作）
• A被pivot分为两部分，继续对剩下的两部分做同样的处理
• 直到所有子集元素不再需要进行上述步骤

void QuickSort(R[], int lo, int hi)
{
    将lo, hi用i, j两个副本进行拷贝（**
    声明基准;
    if(划分长度大于等于2，即hi > lo)
    {
        取基准为左端端点;//都可
        当hi 不等于 lo时循环;
            当hi > lo且R[hi] > temp时循环;
                hi--（继续往中间靠;
            R[lo] = R[hi];//发现小于基准的替换将其替换到左半区
            当lo < hi且R[lo] < temp时循环;
                lo++(继续往中间靠;
            R[hi] = R[lo];//发现大于基准的将其替换到右半区
        在hi,lo重合处放基准;//数据平衡，循环里有一个数据是直接被覆盖的，就是基准，现在将其添加回数组中
        QuickSort(R[], lo, i - 1);
        QuickSort(R[], i + 1, hi);//递归继续进行快排
        //要是前面没有进行副本拷贝在这里进行递归操作时就不太好判断边界了。
    }
}

void QuickSort(int R[], int lo, int hi){
    int i = lo, j = hi;
    int temp;
    if(i < j){
        temp = R[i];
        while (i != j)
        {
            while(j > i && R[j] > temp)-- j;
            R[i] = R[j];
            while(i < j && R[i] < temp)++ i;
            R[j] = R[i];
        }
        R[i] = temp;
        QuickSort(R, lo, i - 1);
        QuickSort(R, i + 1, hi);
    }
}

 

 

 

 

 

 

 

 

 

https://zhuanlan.zhihu.com/p/93129029