[机器学习]—梯度下降法
机器学习中往往需要刻画模型与真实值之间的误差,即损失函数,通过最小化损失函数来获得最优模型。这个最优化过程常使用梯度下降法完成。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。
1. 梯度
解释梯度之前需要解释导数与偏导数。导数与偏导数的公式如下:
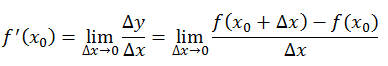
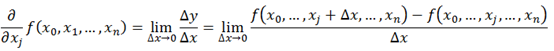
导数与偏导数都是自变量趋于0时,函数值的变化量与自变量的变化量的比值,反应了函数f(x)在某一点沿着某一方向的变化率。导数中该方向指的是x轴正方向,偏导数中指的是向量x所在空间中一组单位正交基()中某一个基方向的变化率。因为x的坐标已知,所以这组正交基唯一,也就是表示x的坐标轴,而偏导数就是因变量与自变量在x的坐标轴正方向的变化量之比。
上面叙述的变化率都是函数在某一点上函数沿特定方向的变化率,如导数中指x轴正方向,偏导数中指自变量x所在空间中一组正交基的某一个方向。那么如何表示因变量变化量在某一点沿任意方向上与自变量变化量的比值呢?这里就需要使用方向导数,方向导数定义如下。
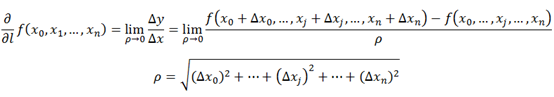
偏导数是函数某一点沿着任意方向上因变量与自变量的变化率的比值,是一个向量,有大小也有方向,那么既然偏导数既有大小也有方向,则肯定存在一个偏导数,其模值(即大小)最大。这个最大的模值就是梯度的模值,模值最大的偏导数的方向就是梯度的方向。梯度的定义如下:
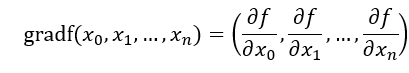
2. 梯度下降
前面说到梯度方向是函数最大偏导数的方向,因此沿着与该方向相反的方向,必然可以达到函数的一个极小值点。以一元函数为例,其导数方向就是梯度方向,因此为了求取如下图所示的函数的极小值,只需要沿着导数相反的反向向下递归即可。如图所示,计算起点在一个较高的点,计算当前点梯度,沿着与梯度相反的方向一步步向下进行,最终会达到函数的极小值点。
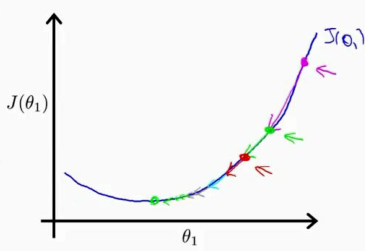
然后图中的情况比较特殊,因为图中函数只有一个极值点,这个极值点也就是函数的最小值点,因此梯度下降法递归到极值点后,也就得到了函数的最小值。但是如果函数存在多个极小值点(非凸函数),使用梯度下降法可能使算法陷入局部最小值点,从而得不到全局最优解。
3. 梯度下降法推导
梯度下降法一般用于机器学习算法中,用于最小化损失函数,得到最优的预测模型,这个预测模型就是假设函数,对于线性回归来说,一般为以下形式:
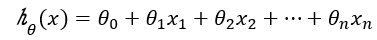
写成矩阵形式:
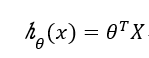
其中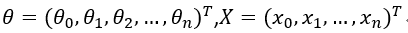
线性回归中损失函数常使用模型预测值与真实值差值的平方刻画,如下:
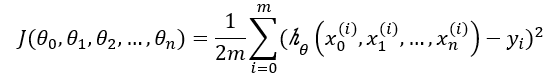
其中m为训练样本的个数,即批梯度下降法中损失函数等于所有样本单独产生的损失(误差)之和。
写成矩阵形式有
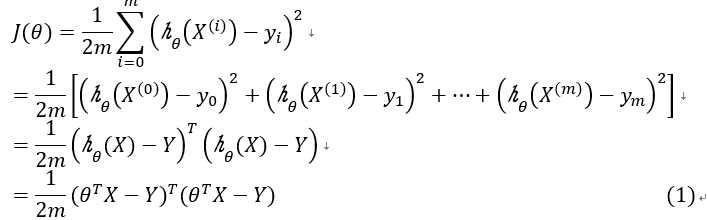
其中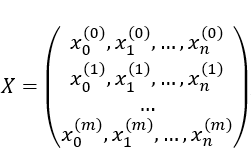 是一个mxn矩阵,矩阵每一行都是一个输入向量,机器学习中每一行即为一个输入样本的特征
是一个mxn矩阵,矩阵每一行都是一个输入向量,机器学习中每一行即为一个输入样本的特征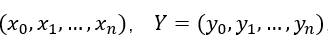 ,每个点即为输入样本对应的标签。
,每个点即为输入样本对应的标签。
为了使用梯度下降法计算的最小值,需要先计算损失函数关于的的偏导数,根据矩阵的求导公式,有下式成立:
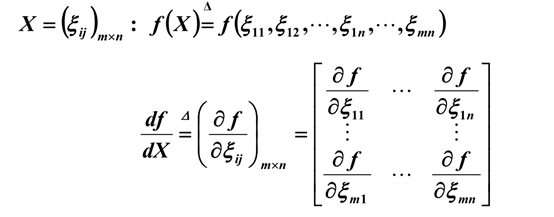
因为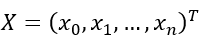 ,则:
,则:
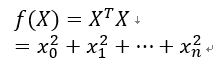
所以:
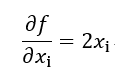
于是对于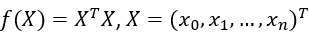 ,有:
,有:
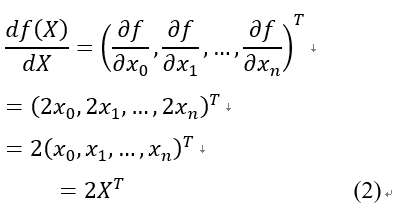
对于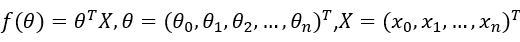 则有:
则有:
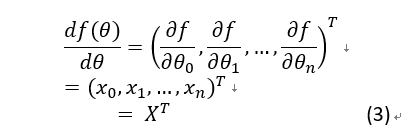
根据式(2)式(3)及链式法则,可得:
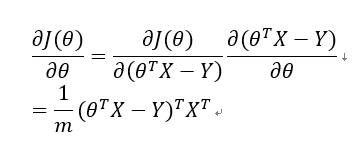
上式即为损失函数对于参数的导数,根据梯度下降法,设算法学习率为,则参数的更新策略为:
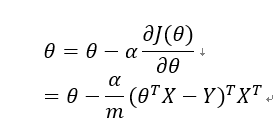
4. 几种常见的梯度下降法
式(1)为模型的损失函数,矩阵形式的损失函数中,为mxn大小的矩阵,从代数形式的损失函数定义中,可知m为梯度下降法一次输入的样本个数,n为样本特征向量的个数,几种梯度下降法就是以m的个数来区分的,分别为:、
1) 批量梯度下降法。这种情况下m为所有训练样本的大小,即一次将所有样本特征向量模型中,并根据模型结果,计算损失函数,更新参数,直到达到设定的最优解条件。优点是可以利用所有样本的数据,计算全局梯度,,从而减小算法了陷入局部极小值情况的出现。而且由于批量梯度下降法使用了所有样本的信息,算法进行梯度下降时,计算的方向与实际样本空间中梯度方向相近,使得算法能较快收敛;缺点是计算量大,计算速度慢,对于海量数据集,可能出现内存不足的情况。
2) 随机梯度下降法。批量梯度下降法中一次性用矩阵乘法将所有样本的特征向量代入模型中计算,而随机梯度下降法与之相反,每次只取一个样本代入模型计算更新参数,即m=1,这个样本通过随机的方式从输入样本中选择。这种方法优点是计算速度快;缺点是一次只使用一个样本进行计算梯度,则每次迭代的过程中,算法梯度下降的方向受当前样本影响极大(梯度下降时并不能总沿着真实梯度方向进行,而是四处乱撞,因为每个样本对应的梯度可能会有很大的差别,如前一个样本计算梯度方向0°,算法沿着0°的方向运行,然后当前样本计算得到梯度方向为150°,则算法又会往刚才几乎相反的方向运行,产生震荡),会造成震荡,使算法收敛速度减慢,还有可能使算法陷入局部极小值,得不到最优解。
3) 小批量梯度下降法。前两种梯度下降法都较为极端,实际运用中常从样本空间中选取一部分样本(一个batch)作为输入,计算一次后再选择一部分样本输入,计算更新参数,直到满足梯度条件。这种算法兼顾了批量梯度下降法和随机梯度下降法的优点,实际应用中常使用这种方法。
参考:
1.梯度下降(Gradient Descent)小结:https://www.cnblogs.com/pinard/p/5970503.html
2. ML重要概念:梯度(Gradient)与梯度下降法(Gradient Descent): https://blog.csdn.net/walilk/article/details/50978864
3. 梯度下降百度百科: https://baike.baidu.com/item/梯度下降/4864937?fr=aladdin
4. 梯度百度百科: https://baike.baidu.com/item/梯度/13014729?fr=aladdin
5. 张凯院:《矩阵论》
作者:Brccq
出处:http://www.cnblogs.com/br170525//
出处:http://www.loveyfyq.com//
欢迎转载,必须在文章页面明显位置给出原文连接,如需本博文源代码或者有任何问题,请在博文留下您的邮箱或者问题说明。



