算法分析---------------------Floyd算法

-------------------

Floyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。

 

 

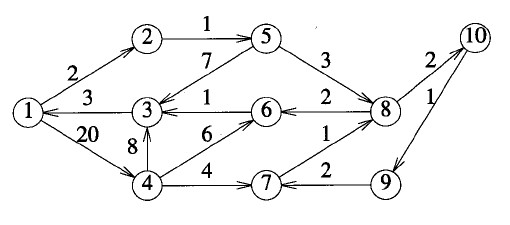
对上面这个图的程序

 

/*
 * main.cpp
 *
 *  Created on: 2013-8-18
 *      Author: 白强
 */

#include <iostream>
using namespace std;

const int INF = 100000;
int n = 10, map[11][11], dist[11][11][11];
//初始化路径
void init() {
    int i, j;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            map[i][j] = (i == j) ? 0 : INF;
    map[1][2] = 2, map[1][4] = 20, map[2][5] = 1;
    map[3][1] = 3, map[4][3] = 8, map[4][6] = 6;
    map[4][7] = 4, map[5][3] = 7, map[5][8] = 3;
    map[6][3] = 1, map[7][8] = 1, map[8][6] = 2;
    map[8][10] = 2, map[9][7] = 2, map[10][9] = 1;
}
//核心算法
void floyd_dp() {
    int i, j, k;
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            dist[i][j][0] = map[i][j];
    for (k = 1; k <= n; k++)
        for (i = 1; i <= n; i++)
            for (j = 1; j <= n; j++) {
                dist[i][j][k] = dist[i][j][k - 1];
                if (dist[i][k][k - 1] + dist[k][j][k - 1] < dist[i][j][k])
                    dist[i][j][k] = dist[i][k][k - 1] + dist[k][j][k - 1];
            }
}
int main() {
    int k, u, v;
    init();
    floyd_dp();
    while (cin >> u >> v, u || v) {
        for (k = 0; k <= n; k++) {
            if (dist[u][v][k] == INF)
                cout << "+∞" << endl;
            else
                cout << dist[u][v][k] << endl;
        }
    }
    return 0;
}

---

 输出结果

1 3
+∞
+∞
+∞
+∞
28
10
10
10
9
9
9