图解算法习题之老王的杂货铺
原题：老王开杂货店想送N块冬瓜糖砖给客户，每块冬瓜糖砖长宽高都是10厘米。老王希望将这N块冬瓜糖砖包成一大包（x*y*z的长方体），以方便运送，但为了响应环保，希望使用的包装纸越少越好。编写一个程序输入N，输出最少的包装纸面积。
上面的题目可以简化为：将N块体积为1的正方体堆成长方体，求最小面积。
在不用大量数据看规律的情况下，我是这么思考的。（因为看数据没看出有什么规律。。。。。。）
长方体表面积公式：S = 2（x*y+x*z+y*z）,当且仅当x=y=z的时候，表面积最小。但是边长是整数，这种情况很少存在，所以我们只要找到各个边长差绝对值的和最小的边长即可。
但是怎么将小正方体的个数，分成长宽高呢？分解质因数。废话不多少，直接上代码。可以先运行看看，然后再看代码。
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>分解质因数</title>
</head>
<body>
个数：<input type="text" id="inp"/><br>
质因数：<span id="zys"></span><br>
最小表面积：<span id="bmj"></span><br>
<!-- <input type="button" value="求质因数" onclick="getZys()"/> -->
<input type="button" value="求最小表面积" onclick="getBmj()"/>
<script>
function getZys(){
var n = Number(document.getElementById("inp").value);
var zys = new Array(); //质因数
var num = 0;
var m = n;
for(var i = 2; i <= n; i++){
if(n % i == 0){
zys[num] = i;
num++;
n = (n/i);
i--;
}
}
if (num < 2)
document.getElementById("zys").innerHTML = m + "为质数";
else {
var out = m + "=" + zys[0];
for (var k = 1; k < num; k++) {
out += "*" + zys[k];
}
document.getElementById("zys").innerHTML = out;
console.log(m+"共有"+num+"个质因数");
}
}
function getBmj(){
getZys();
var n = Number(document.getElementById("inp").value);
var zys = new Array(); //质因数
var num = 0;
var m = n;
var bmj;
for(var i = 2; i <= n; i++){
if(n % i == 0){
zys[num] = i;
num++;
n = (n/i);
i--;
}
}
var scfg = Math.pow(m,1/3); //开三次方(有误差，精准的请用math.js)
if (num < 2){ //排成一条线
bmj = m * 4 + 2;
}else if(Math.floor(scfg) === scfg){ //正方体
bmj = scfg * scfg * 6;
}else{
if(num == 2){ //两个质因数,1为其中的一个边长
bmj = 2 * (zys[0] + zys[1] + zys[0] * zys[1]);
}else if(num == 3){ //3个质因数,三个边长
bmj = 2 * (zys[0]*zys[1] + zys[0] * zys[2] + zys[1]*zys[2]);
}else{ //多个质因数
/*需要组合了，组合成三个边长，将三个边长之差的绝对值相加，最小的那组作为边长*/
/*组合应该可以用循环写出来，但还没想好怎么写*/
bmj = "肉眼组合";
}
}
document.getElementById("bmj").innerHTML = bmj;
}
</script>
</body>
</html>
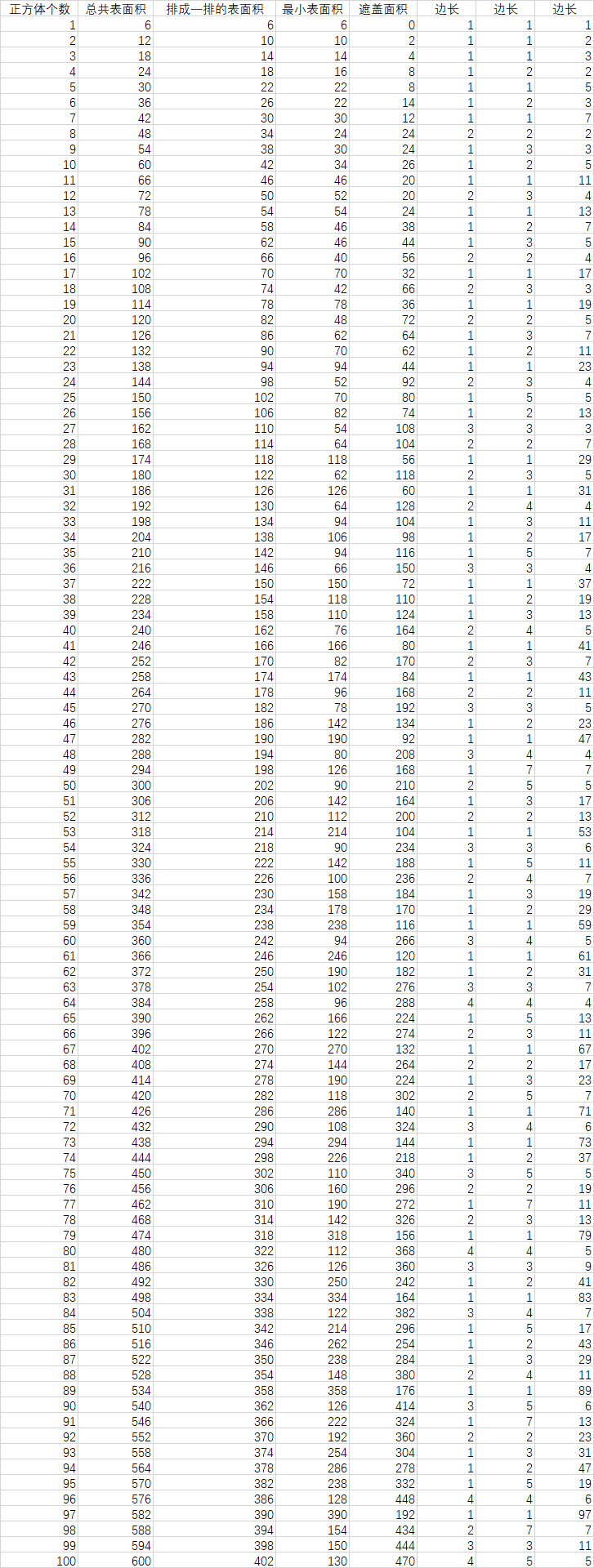
上面的代码是不完整的，对于质因子个数大于3个的情况，我只能想到组合了，目前没想到什么其他的方法。但是组合还没想好怎么写，还请各大牛人指导一下，顺便给编辑部提提意见，出了题最起码给个答案啊。我也比对过数据，我是没看出规律，可以贡献出来，给大家看看。
