B-generator 1_2019牛客暑期多校训练营（第五场）

题意

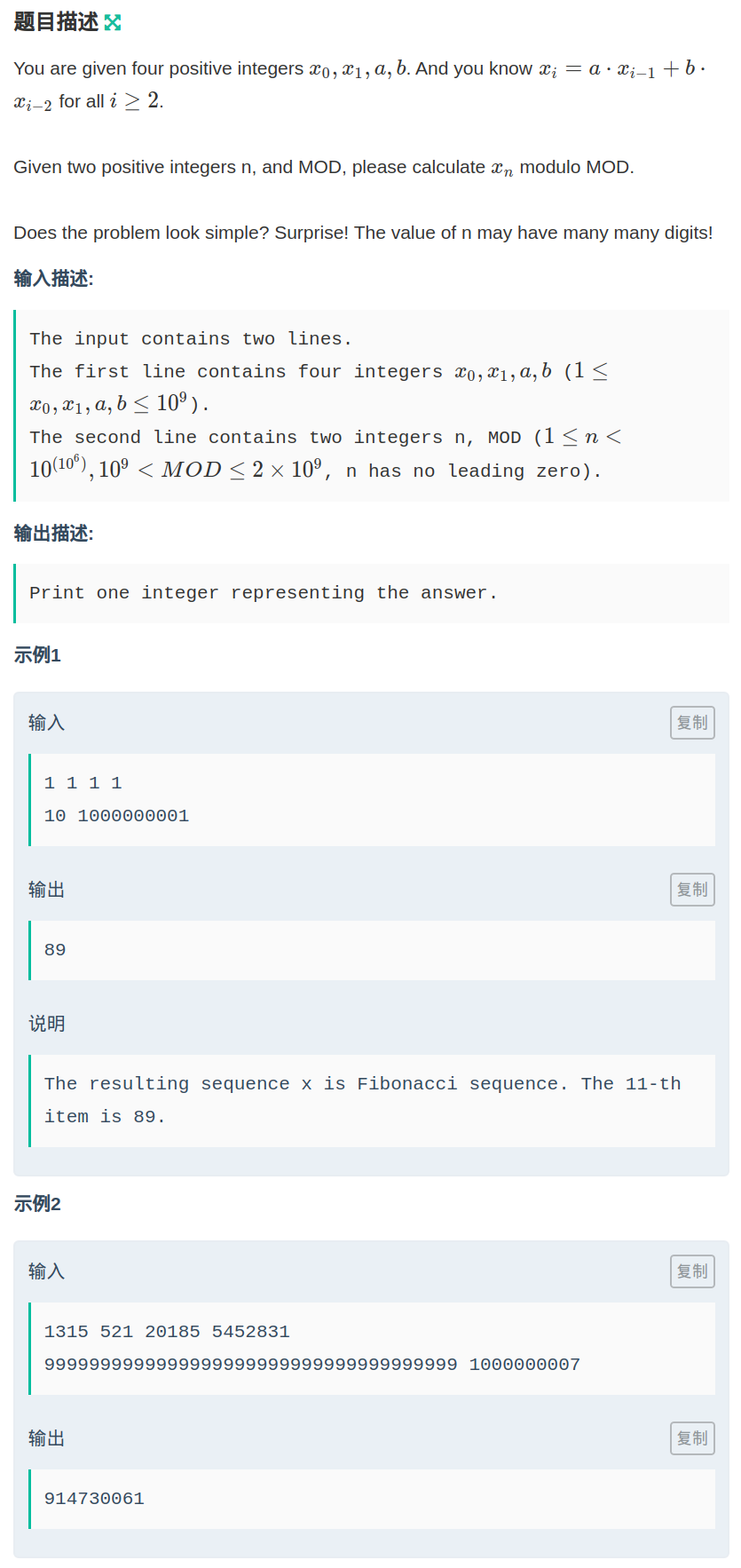
给出\(x0,x1,a,b\)， \(x_i = a\cdot x_{i-1} + b\cdot x_{i-2}\)，问\(x_n取模mod\)

题解

用十进制快速幂，二进制快速幂是每到下一位就把a平方，十进制快速幂就是每到下一位就把a变成\(a^{10}\)，乘10次方的过程再用二进制快速幂优化，总体复杂度就是\(O(\log_{10}{n}\cdot \log_2{10})\)

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int mx = 1e6+5;
ll mod, x0, x1, a, b;
struct mat {
    ll a[2][2];
    mat() {
        clear();
        a[0][0] = 1;
        a[1][1] = 1;
    }
    void clear() {memset(a, 0, sizeof(a));}

    mat operator * (mat other) {
        mat tmp;
        tmp.clear();
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                for (int k = 0; k < 2; k++) {
                    //printf("%d %d %d\n", tmp.a[i][j], a[i][k], other.a[k][j]);
                    tmp.a[i][j] += a[i][k] * other.a[k][j] % mod;
                    tmp.a[i][j] %= mod;
                }
            }
        }
        return tmp;
    }

    mat operator ^ (int y) {
        mat ans = mat();
        mat x = *this;
        while (y > 0) {
            if (y & 1) ans = ans * x;
            x = x * x;
            y /= 2;
        }
        return ans;
    }

    void show() {
        for (int i = 0; i < 2; i++)
            for (int j = 0; j < 2; j++)
                printf("%d%c", a[i][j], j==1?'\n':' ');
    }
};

char str[mx];

int main() {
    scanf("%lld%lld%lld%lld", &x0, &x1, &a, &b);
    scanf("%s%lld", str, &mod);
    mat base;
    base.a[0][0] = a; base.a[0][1] = 1;
    base.a[1][0] = b; base.a[1][1] = 0;
    
    int len = std::strlen(str);
    
    mat res = mat();
    for (int i = len-1; i >= 0; i--) {
        if (str[i] != 0) {
            res = res * (base ^ (str[i]-'0'));
        }
        base = base ^ 10;
    }
    //res.show();
    ll ans = x1 * res.a[0][1] + x0 * res.a[1][1];
    ans = (ans % mod + mod) % mod;
    printf("%lld\n", ans);
    
    return 0;
}