CNN-权重参数初始化
原地址
https://www.bilibili.com/video/BV1ba411m72B
1.为什么需要对权重初始化精心设计
- 1.容易出现梯度消失(梯度特别的接近0)和梯度爆炸(梯度特别的大)的情况,导致大部分反向传播得到的梯度不起作用或者起反作用
2.设计思路
神经网络的每层的数据的传送是要有意义的
意义体现在我原本表达的意思,不能经过传递之后就曲解了,比如某句话传着传着变谣言
例如小学一个班男孩的身高是一个分布,有一个方差
过了若干年后聚会
这批男孩的身高是一个新分布,有一个新方差
方差描述的是这批数据分布的紧密程度
如果是同一批男孩,那么他们身高的分布大致不会变
所以我们用方差来衡量神经网络的输入到底和输出是不是同一分布
3.是否可以全零初始化,小值初始化,大值初始化?
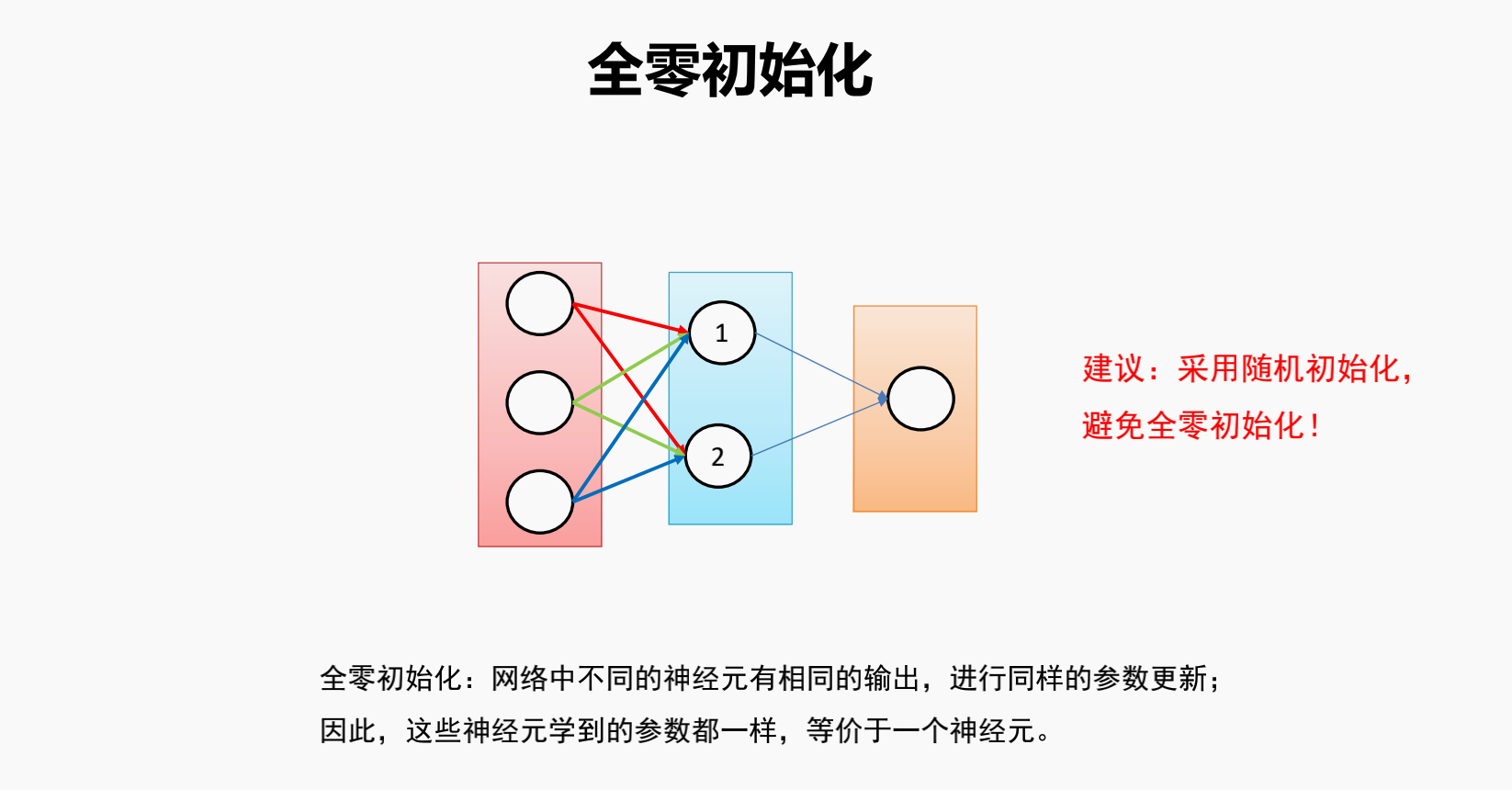
全零初始化
每层输出都一样,因此无论网络训练多少轮
对于每一层中的各个神经元,weights都是相同的,无法学习(提取)到不同的特征
点击查看代码
import numpy as np
from matplotlib import pyplot as plt
def init_weights(u, a0, a1=None, a2=None, a3=None, a4=None):
a_1 = a1 or a0
a_2 = a2 or a0
a_3 = a3 or a0
a_4 = a4 or a0
W0 = np.random.normal(u, a0, 400).reshape(2, 200)
W1 = np.random.normal(u, a_1, 60000).reshape(200, 300)
W2 = np.random.normal(u, a_2, 120000).reshape(300, 400)
W3 = np.random.normal(u, a_3, 120000).reshape(400, 300)
W4 = np.random.normal(u, a_4, 600).reshape(300, 2)
return W0, W1, W2, W3, W4
def sigmoid(x):
return 1 / (1 + np.exp(-x)) # 定义sigmoid函数
def derivative_sigmoid(x):
return x * (1 - x)
def relu(x):
return np.maximum(x, 0)
def leaky_relu(x, p=0.1):
return np.maximum(x, p*x)
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
def derivative_tanh(x):
return 1-tanh(x)**2
def model(X, W0, W1, W2, W3, W4, act='tanh'): # 定义模型的前向传播过程
if act == 'tanh':
output_0 = tanh(X @ W0) # [n, 2] @ [ 2, 200] = [n, 200]
# print(X.shape, W0.shape, output_0.shape)
output_1 = tanh(output_0 @ W1) # [n, 200] @ [200, 300] = [n, 300]
# print(output_0.shape, W1.shape, output_1.shape)
output_2 = tanh(output_1 @ W2) # [n, 300] @ [300, 400] = [n, 400]
# print(output_1.shape, W2.shape, output_2.shape)
output_3 = tanh(output_2 @ W3) # [n, 400] @ [400, 300] = [n, 300]
# print(output_2.shape, W3.shape, output_3.shape)
output_4 = tanh(output_3 @ W4) # [n, 300] @ [300, 2] = [n, 2]
# print(output_3.shape, W4.shape, output_4.shape)
elif act == 'relu':
output_0 = relu(X @ W0)
output_1 = relu(output_0 @ W1)
output_2 = relu(output_1 @ W2)
output_3 = relu(output_2 @ W3)
output_4 = relu(output_3 @ W4)
elif act == 'leaky_relu':
output_0 = leaky_relu(X @ W0)
output_1 = leaky_relu(output_0 @ W1)
output_2 = leaky_relu(output_1 @ W2)
output_3 = leaky_relu(output_2 @ W3)
output_4 = leaky_relu(output_3 @ W4)
else:
output_0 = sigmoid(X @ W0)
output_1 = sigmoid(output_0 @ W1)
output_2 = sigmoid(output_1 @ W2)
output_3 = sigmoid(output_2 @ W3)
output_4 = sigmoid(output_3 @ W4)
return [output_0, output_1, output_2, output_3, output_4]
def plot_hist(outputs, xlim=(-1, 1), ylim=(0, 1)):
n = len(outputs)
fig, axes=plt.subplots(1, n, figsize=(3*n, 3), sharex=True, sharey=True)
for i in range(n):
axes[i].hist(outputs[i].flatten(),bins=50,histtype="stepfilled",density=True,alpha=0.6)
plt.xlim(*xlim)
plt.ylim(*ylim)
plt.show()
W0, W1, W2, W3, W4 = init_weights(0, 0)
X = np.random.normal(0, 1, 1000).reshape(-1, 2) # 初始化X,用于下面所有测试
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-1, 1), ylim=(0, 1))
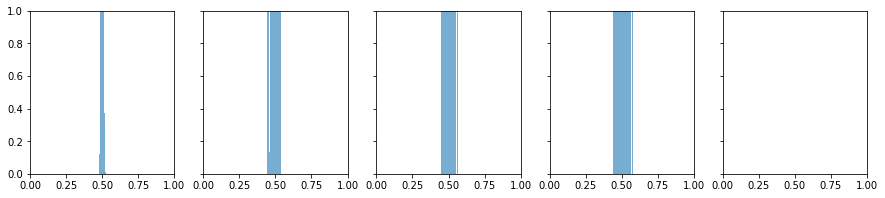
小一点的随机权值初始化
保证了更新不是相同的
但几乎聚集0,信息仍然传不过去,局部梯度也为0,梯度太小
梯度传不过去!!!

点击查看代码
W0, W1, W2, W3, W4 = init_weights(0, 0.01)
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-1, 1), ylim=(0, 1))
outputs = model(X, W0, W1, W2, W3, W4, 'sigmoid')
plot_hist(outputs, xlim=(0, 1), ylim=(0, 1))

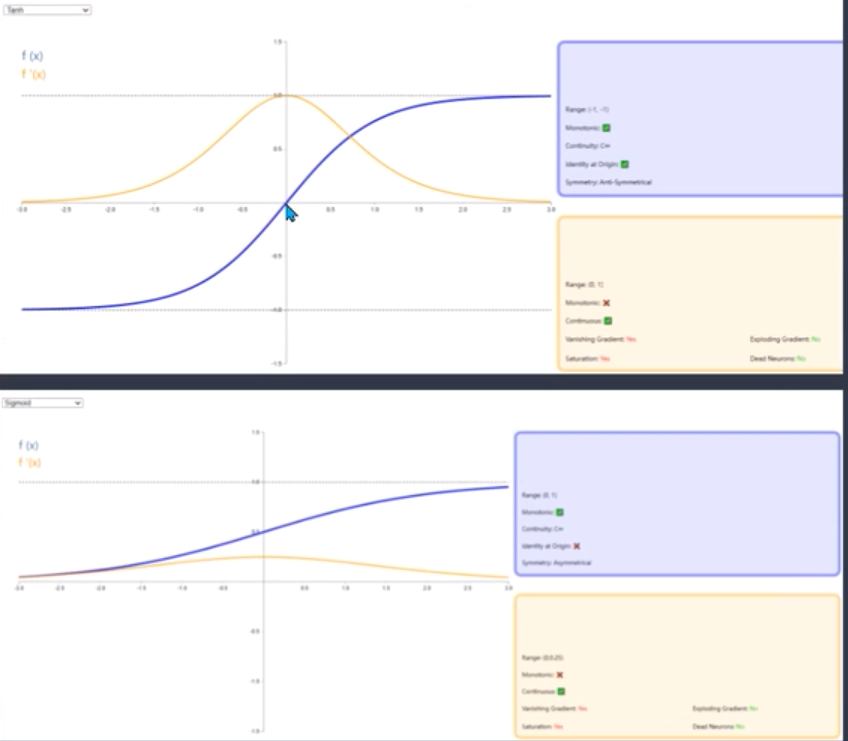
大一点的值初始化
信息传过去了部分,但由于tanh函数的作用,值太大就饱和了,梯度太小
容易饱和,梯度传不回来!!!

点击查看代码
W0, W1, W2, W3, W4 = init_weights(0, 1)
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-1, 1), ylim=(0, 1))
outputs = model(X, W0, W1, W2, W3, W4, 'sigmoid')
plot_hist(outputs, xlim=(0, 1), ylim=(0, 1))



目标:输入的分布z尽量和输出的分布y有相同的分布!!!!
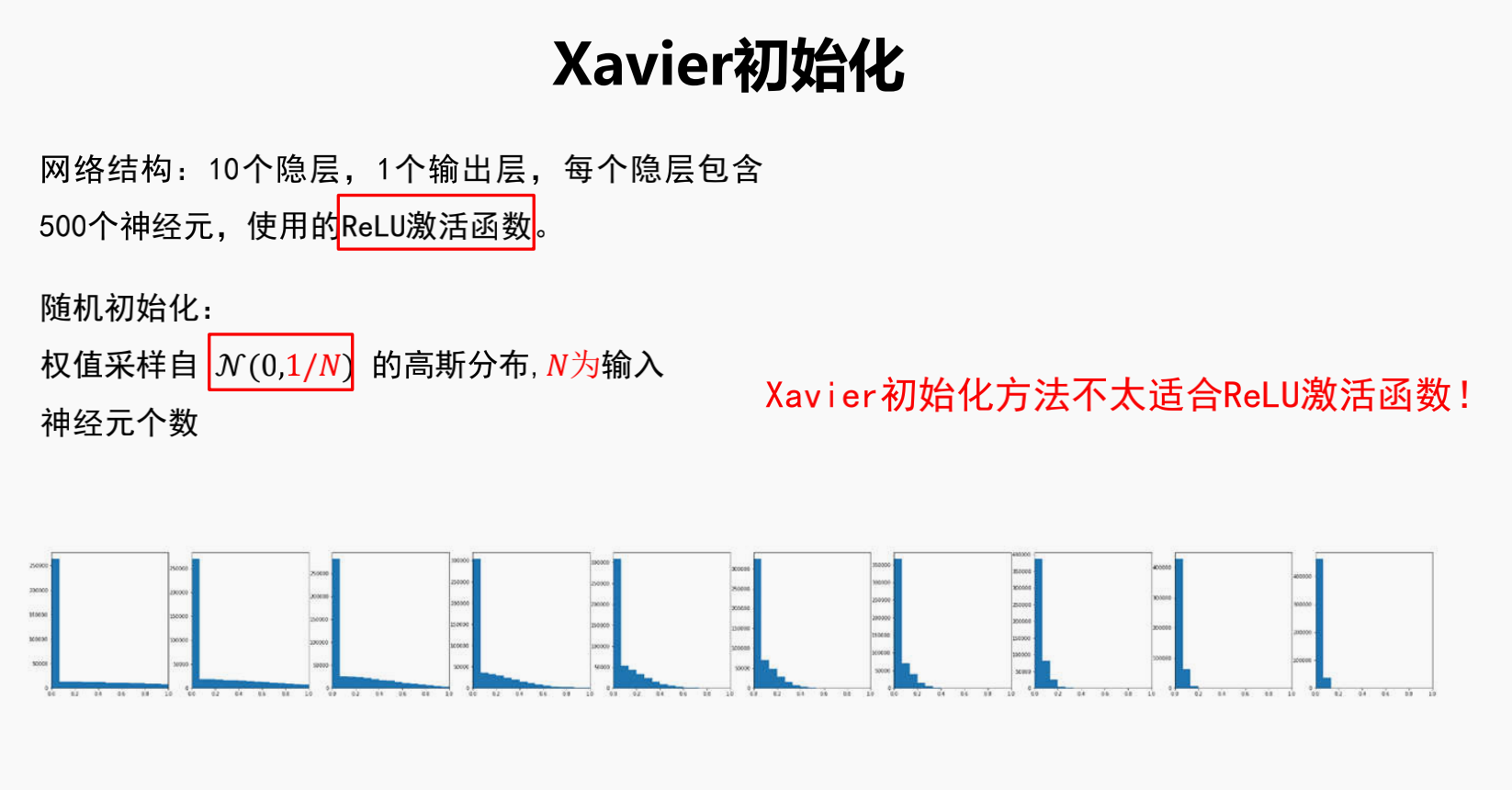
4.Xavier初始化

这个公式有点问题,累加符号应该再套一个大括号,把里面的三项包起来

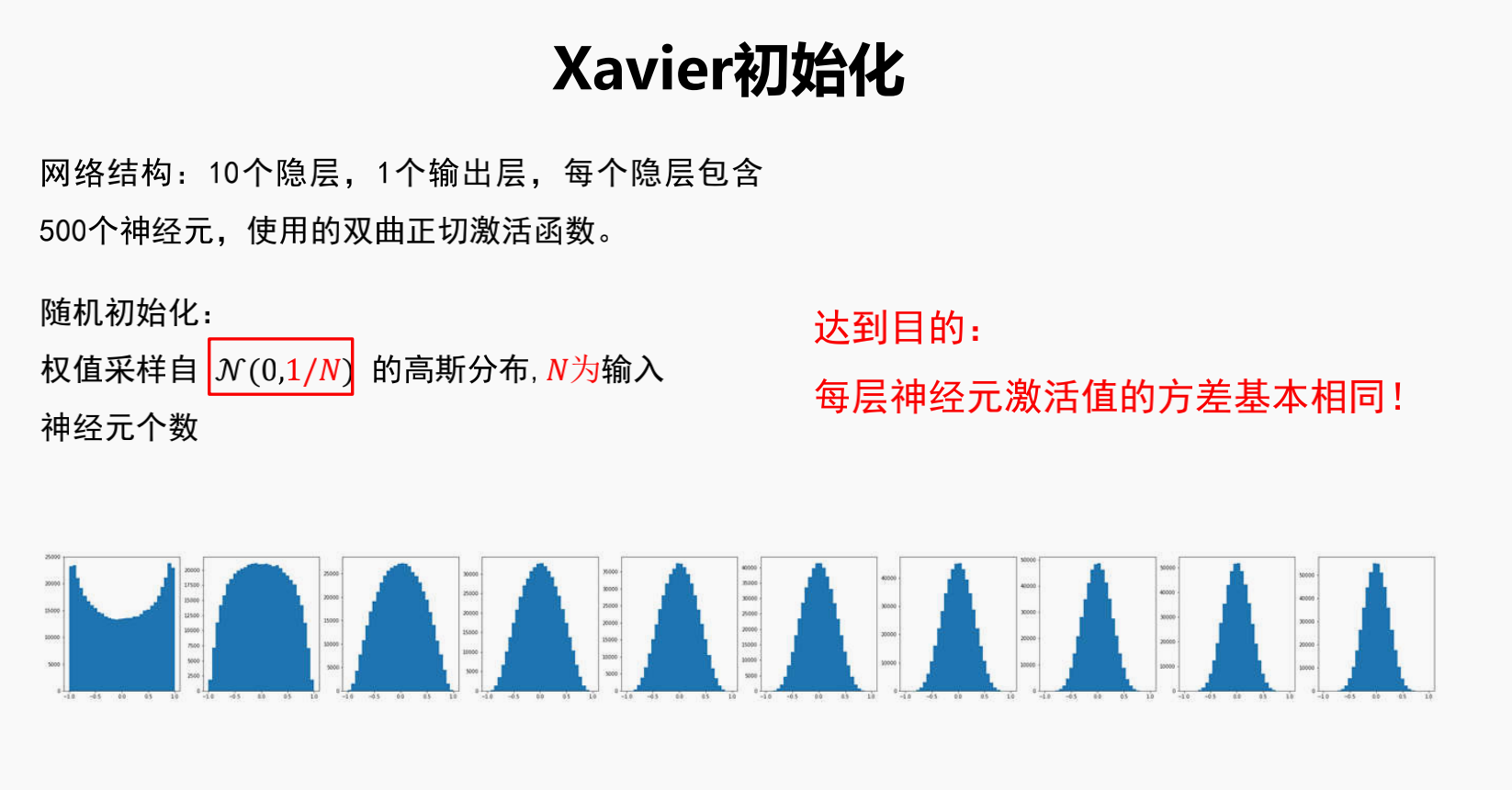
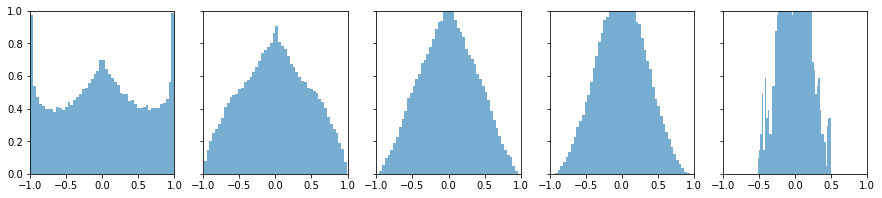
sigmoid/tanh激活函数验证
点击查看代码
# 这里传入的参数是输入数据维度的标准差的倒数,因为numpy创建正态分布是靠标准差来创建的
W0, W1, W2, W3, W4 = init_weights(0, (1/2)**0.5, (1/200)**0.5, (1/300)**0.5, (1/400)**0.5, (1/300)**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-1, 1), ylim=(0, 1))
outputs = model(X, W0, W1, W2, W3, W4, 'sigmoid')
plot_hist(outputs, xlim=(0, 1), ylim=(0, 1))
# 明显看到分布基本上是属于正太分布,数据正向传播通畅
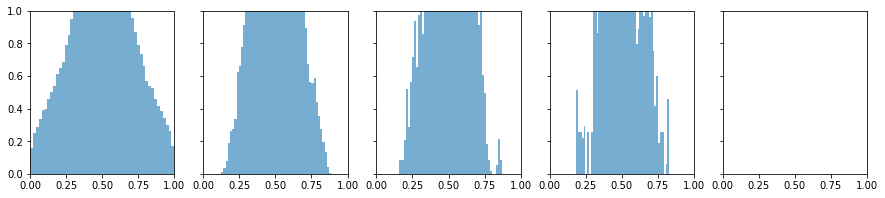
光考虑正向传播是不够的,我们还要考虑反向传播更新梯度
如果效果比较理想,那么应当是输入是什么样的就能传过去什么样,从右往左反向传播
注意此时是从右往左看
点击查看代码
W0, W1, W2, W3, W4 = init_weights(0, (1/2)**0.5, (1/200)**0.5, (1/300)**0.5, (1/400)**0.5, (1/300)**0.5)
lr = 0.01
epochs = 1
Y_onehot = [] # 随机生成一个y标签的独热编码,因为要用于计算损失反向传播更新梯度
for i in range(X.shape[0]):
temp = np.random.randint(0, 2)
Y_onehot.append([temp, abs(1-temp)])
Y_onehot = np.array(Y_onehot)
for epoch in range(epochs):
for j in range(X.shape[0]):
[output_0, output_1, output_2, output_3, output_4] = model(X[j], W0, W1, W2, W3, W4, 'tanh')
# 反向传播计算梯度, 梯度的维度和权重维度相同,因为等会要更新权重
loss_4 = derivative_tanh(output_4) * (Y_onehot[j] - output_4)
grad_4 = output_3.reshape(-1,1) @ loss_4.reshape(1,-1)
loss_3 = derivative_tanh(output_3) * (W4 @ loss_4)
grad_3 = output_2.reshape(-1,1) @ loss_3.reshape(1,-1)
loss_2 = derivative_tanh(output_2) * (W3 @ loss_3)
grad_2 = output_1.reshape(-1,1) @ loss_2.reshape(1,-1)
loss_1 = derivative_tanh(output_1) * (W2 @ loss_2)
grad_1 = output_0.reshape(-1,1) @ loss_1.reshape(1,-1)
loss_0 = derivative_tanh(output_0) * (W1 @ loss_1)
grad_0 = X[j].reshape(-1,1) @ loss_0.reshape(1,-1)
# 梯度更新
W4 += lr*grad_4
W3 += lr*grad_3
W2 += lr*grad_2
W1 += lr*grad_1
W0 += lr*grad_0
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-0.5, 0.5), ylim=(0, 4))
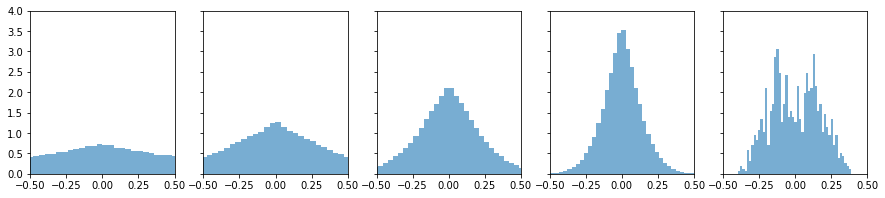
显然从右往左看,反向传播的信息是不能够很好的传递的,所以Xavier重新考虑反向传播

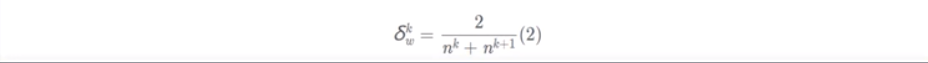
结论,折中正向传播和反向传播
首先验证权重初始化的方差是按照输入维度和输出维度之和的倒数的2倍 2/(Nin+Nout)
用tanh和sigmoid验证
如果效果比较理想,那么应当是输入是什么样的就能传过去什么样
点击查看代码
# 这里传入的参数是输入数据维度的标准差的倒数,因为numpy创建正态分布是靠标准差来创建的
W0, W1, W2, W3, W4 = init_weights(0, (2/(2+200))**0.5, (2/(200+300))**0.5, (2/(300+400))**0.5, (2/(400+300))**0.5, (2/(300+2))**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-0.75, 0.75), ylim=(0, 1))
# 明显看到分布基本上是属于正太分布,数据正向传播通畅
lr = 0.01
epochs = 1
for epoch in range(epochs):
for j in range(X.shape[0]):
[output_0, output_1, output_2, output_3, output_4] = model(X[j], W0, W1, W2, W3, W4, 'tanh')
# 反向传播计算梯度, 梯度的维度和权重维度相同,因为等会要更新权重
loss_4 = derivative_tanh(output_4) * (Y_onehot[j] - output_4)
grad_4 = output_3.reshape(-1,1) @ loss_4.reshape(1,-1)
loss_3 = derivative_tanh(output_3) * (W4 @ loss_4)
grad_3 = output_2.reshape(-1,1) @ loss_3.reshape(1,-1)
loss_2 = derivative_tanh(output_2) * (W3 @ loss_3)
grad_2 = output_1.reshape(-1,1) @ loss_2.reshape(1,-1)
loss_1 = derivative_tanh(output_1) * (W2 @ loss_2)
grad_1 = output_0.reshape(-1,1) @ loss_1.reshape(1,-1)
loss_0 = derivative_tanh(output_0) * (W1 @ loss_1)
grad_0 = X[j].reshape(-1,1) @ loss_0.reshape(1,-1)
# 梯度更新
W4 += lr*grad_4
W3 += lr*grad_3
W2 += lr*grad_2
W1 += lr*grad_1
W0 += lr*grad_0
outputs = model(X, W0, W1, W2, W3, W4, 'tanh')
plot_hist(outputs, xlim=(-0.75, 0.75), ylim=(0, 1))
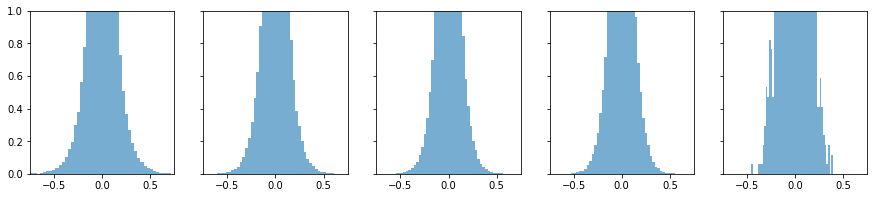
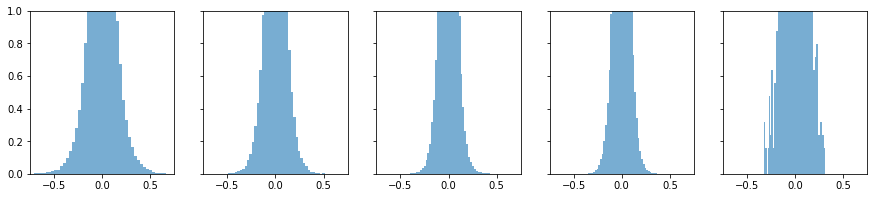
用tanh先进行一次正向传播为上图
学习率0.01,训练一个epoch的反向传播为下图
第一幅图正向传播,从左往右看,信息基本传递
第二幅图反向传播,从右往左看,信息基本传递¶
点击查看代码
# 这里传入的参数是输入数据维度的标准差的倒数,因为numpy创建正态分布是靠标准差来创建的
W0, W1, W2, W3, W4 = init_weights(0, (2/(2+200))**0.5, (2/(200+300))**0.5, (2/(300+400))**0.5, (2/(400+300))**0.5, (2/(300+2))**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'sigmoid')
n = len(outputs)
fig, axes=plt.subplots(1, n, figsize=(3*n, 3), sharex=True, sharey=True)
for i in range(n):
axes[i].hist(outputs[i].flatten(),bins=25,histtype="stepfilled",density=True,alpha=0.6)
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()
# 明显看到分布基本上是属于正太分布,数据正向传播通畅
lr = 0.01
epochs = 1
# Y_onehot = []
# for i in range(X.shape[0]):
# temp = np.random.randint(0, 1)
# Y_onehot.append([temp, abs(1-temp)])
# Y_onehot = np.array(Y_onehot)
for epoch in range(epochs):
for j in range(X.shape[0]):
[output_0, output_1, output_2, output_3, output_4] = model(X[j], W0, W1, W2, W3, W4, 'sigmoid')
# 反向传播计算梯度, 梯度的维度和权重维度相同,因为等会要更新权重
# 最后一层“损失” = 最后一层输出带入sigmoid偏导 * (真实值 - 最后一层输出)
loss_4 = derivative_sigmoid(output_4) * (Y_onehot[j] - output_4)
# 该层梯度 = 上层权重 @ 该层“损失”
grad_4 = output_3.reshape(-1,1) @ loss_4.reshape(1,-1)
# 非最后一层的该层“损失” = 该层输出带入sigmoid偏导 * (下一层权重 - 下一层“损失”)
loss_3 = derivative_sigmoid(output_3) * (W4 @ loss_4)
grad_3 = output_2.reshape(-1,1) @ loss_3.reshape(1,-1)
# 非最后一层的该层“损失” = 该层输出带入sigmoid偏导 * (下一层权重 - 下一层“损失”)
loss_2 = derivative_sigmoid(output_2) * (W3 @ loss_3)
grad_2 = output_1.reshape(-1,1) @ loss_2.reshape(1,-1)
# 非最后一层的该层“损失” = 该层输出带入sigmoid偏导 * (下一层权重 - 下一层“损失”)
loss_1 = derivative_sigmoid(output_1) * (W2 @ loss_2)
grad_1 = output_0.reshape(-1,1) @ loss_1.reshape(1,-1)
loss_0 = derivative_sigmoid(output_0) * (W1 @ loss_1)
grad_0 = X[j].reshape(-1,1) @ loss_0.reshape(1,-1)
# 梯度更新
W4 += lr*grad_4
W3 += lr*grad_3
W2 += lr*grad_2
W1 += lr*grad_1
W0 += lr*grad_0
outputs = model(X, W0, W1, W2, W3, W4, 'sigmoid')
plot_hist(outputs, xlim=(0, 1), ylim=(0, 1))
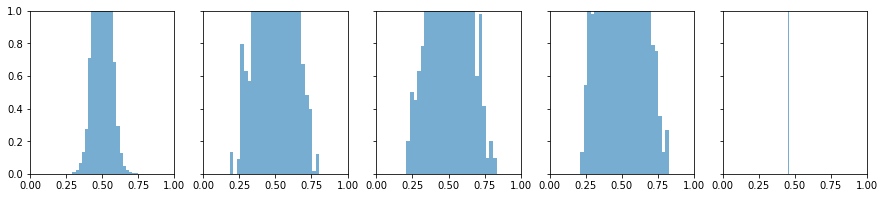
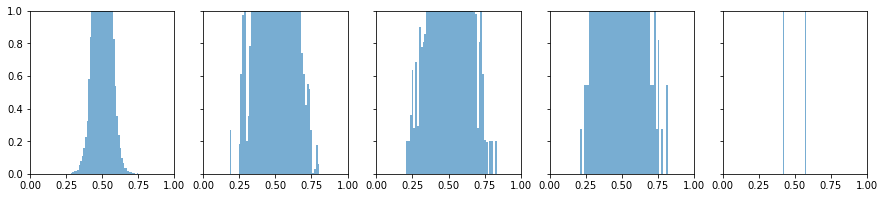
用sigmoid先进行一次正向传播为上图
学习率0.01,训练一个epoch的反向传播为下图
第一幅图正向传播,从左往右看,信息基本传递
第二幅图反向传播,从右往左看,信息基本传递
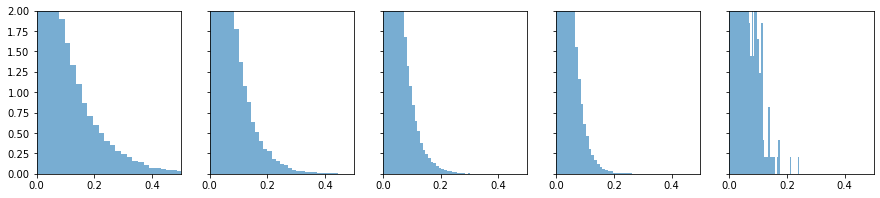
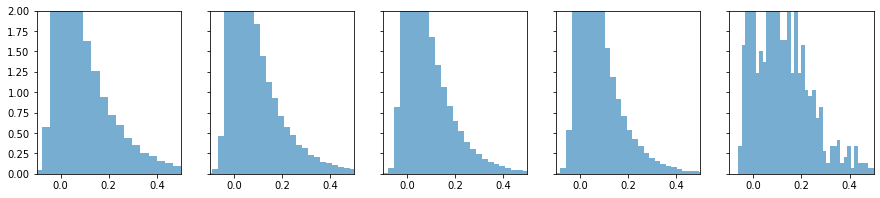
Relu函数不适用Xavier初始化权重方法
因为随机杀死一半,破坏了数据的分布
Relu不会有小于0的数,所以只画了大于0的部分
基本上在第4层时候就没什么信息了¶
点击查看代码
W0, W1, W2, W3, W4 = init_weights(0, (2/(2+200))**0.5, (2/(200+300))**0.5, (2/(300+400))**0.5, (2/(400+300))**0.5, (2/(300+2))**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'relu')
plot_hist(outputs, xlim=(0, 0.5), ylim=(0, 2))
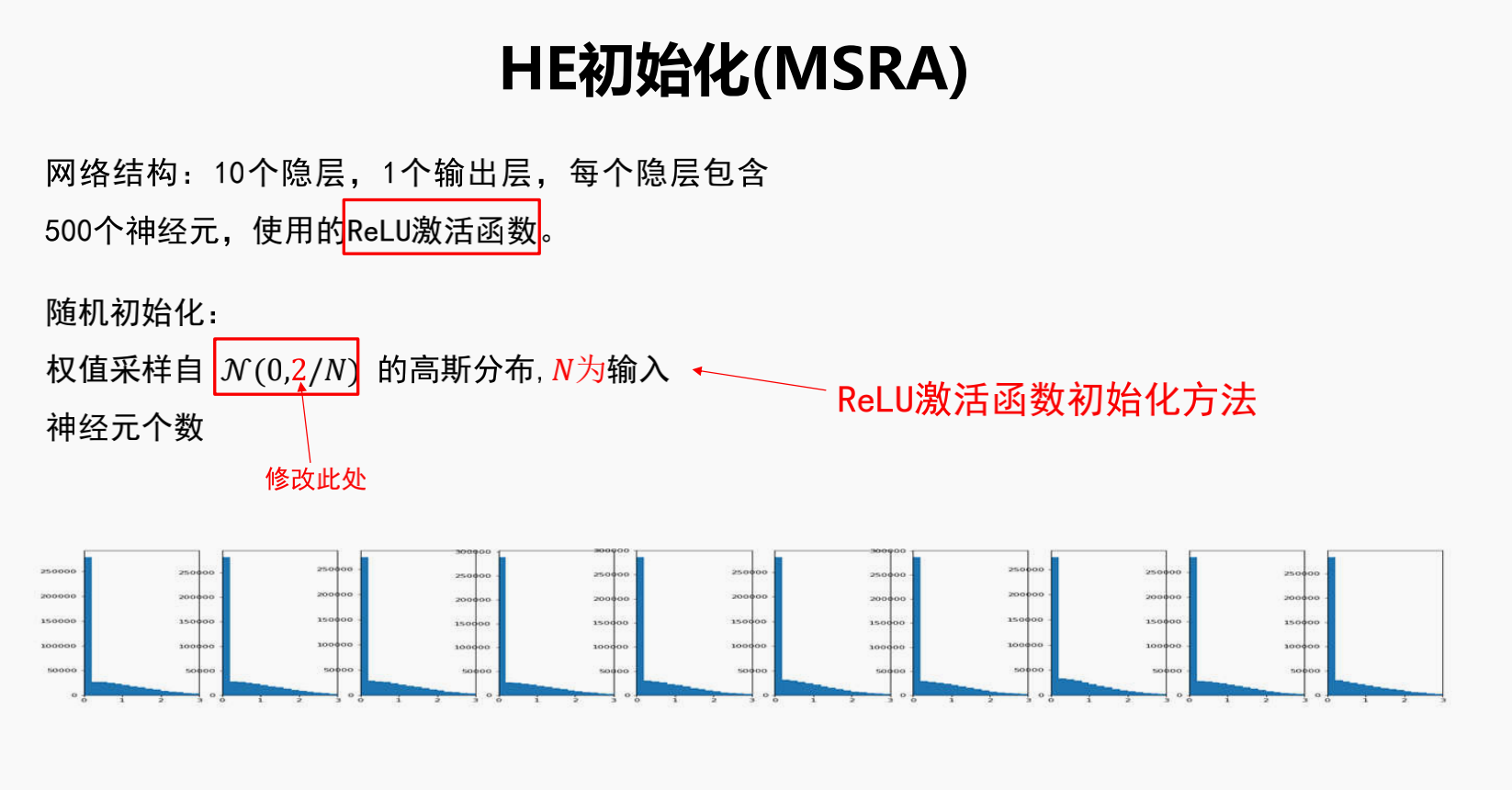
5.何恺明的初始化 He初始化
如果使用Relu函数,则采用何凯明大神的初始化权重方法
仅仅只是将Xavier中方差改为2倍,就能很好的缓和使用Relu的情况
点击查看代码
W0, W1, W2, W3, W4 = init_weights(0, (2*2/(2+200))**0.5, (2*2/(200+300))**0.5, (2*2/(300+400))**0.5, (2*2/(400+300))**0.5, (2*2/(300+2))**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'relu')
plot_hist(outputs, xlim=(0, 0.5), ylim=(0, 2))
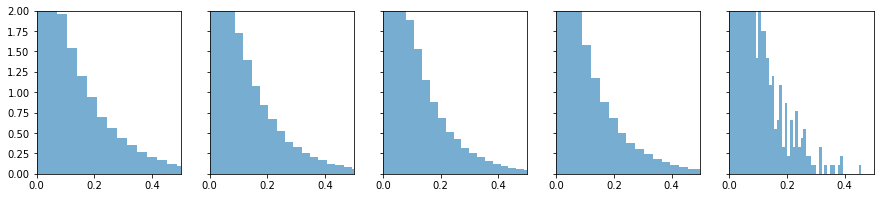
但是这样并不是适用于relu的变体,于是何凯明大神做了一个推广
这里分母的理解是,如果把全体实数R看作2份,那么relu相当于杀死了其中1份,所以a=0
那么leaky relu(a)相当于抑制了一半,抑制的系数a¶
点击查看代码
a = 0.3
W0, W1, W2, W3, W4 = init_weights(0, (2*2/((1+a**2)*(2+200)))**0.5, (2*2/((1+a**2)*(200+300)))**0.5,
(2*2/((1+a**2)*(300+400)))**0.5, (2*2/((1+a**2)*(400+300)))**0.5, (2*2/((1+a**2)*(300+2)))**0.5)
outputs = model(X, W0, W1, W2, W3, W4, 'leaky_relu')
plot_hist(outputs, xlim=(-0.1, 0.5), ylim=(0, 2))
sigmoid和tanh函数用Xavier比较合适,relu和leaky relu用何凯明方法比较合适
点击查看代码
import torch
def cal(x):
return (x.mean(), x.var())
uniform_w = torch.nn.init.uniform_(torch.empty(300, 500), a=0.0, b=1.0)
normal_w = torch.nn.init.normal_(torch.empty(300, 500), mean=0.0, std=1.0)
xavier_uniform_w = torch.nn.init.xavier_uniform_(torch.empty(300, 500), gain=1.0)
kaiming_uniform_w = torch.nn.init.kaiming_uniform_(torch.empty(300, 500), a=0,mode='fan_in',nonlinearity='relu')
xavier_normal_w = torch.nn.init.xavier_normal_(torch.empty(300, 500), gain=1.0)
kaiming_normal_w = torch.nn.init.kaiming_normal_(torch.empty(300, 500), a=0,mode='fan_in',nonlinearity='relu')
kaiming_uniform_w_l = torch.nn.init.kaiming_uniform_(torch.empty(300, 500), a=0.3,mode='fan_in',nonlinearity='leaky_relu')
kaiming_normal_w_l = torch.nn.init.kaiming_normal_(torch.empty(300, 500), a=0.3,mode='fan_in',nonlinearity='leaky_relu')
点击查看代码
print('uniform_w:', cal(uniform_w))
print('normal_w:', cal(normal_w))
print('xavier均匀分布:', cal(xavier_uniform_w))
print('kaiming均匀分布by torch:', cal(kaiming_uniform_w))
print('xavier正态分布:', cal(xavier_normal_w))
print('kaiming正态分布by torch:', cal(kaiming_normal_w))
print('kaiming均匀分布leakyrelu:', cal(kaiming_uniform_w_l))
print('kaiming正态分布leakyrelu by torch:', cal(kaiming_normal_w_l))
uniform_w: (tensor(0.4999), tensor(0.0833))
normal_w: (tensor(-0.0016), tensor(0.9989))
xavier均匀分布: (tensor(0.0001), tensor(0.0025))
kaiming均匀分布by torch: (tensor(7.6385e-05), tensor(0.0040))
xavier正态分布: (tensor(6.1033e-05), tensor(0.0025))
kaiming正态分布by torch: (tensor(7.5544e-05), tensor(0.0040))
kaiming均匀分布leakyrelu: (tensor(-1.6571e-05), tensor(0.0037))
kaiming正态分布leakyrelu by torch: (tensor(-0.0001), tensor(0.0037))

点击查看代码
# 均匀分布的方差是区间长度的平方再除以12
# 何凯明就是在xavier基础上乘了2,但最后有个近似处理,假设输入输出维度一样,便可以约掉2,但可以设置你想要保证正向还是反向。
print('[0, 1]均匀分布的均值与方差', 1/2, (1-0)**2/12)
print('xavier均匀分布的方差', (2*((6/(800))**0.5))**2/12)
print('kaiming均匀分布的方差', (2*((2*6/(800))**0.5))**2/12) # 2*6/(400+400) -> 6/400
print('kaiming均匀分布的方差近似', (2*((6/(500))**0.5))**2/12)
print('xavier正态分布的方差', 2/(800))
print('kaiming正态分布的方差', 2*2/(800)) # 2*2/(400+400) -> 2/400
print('kaiming正态分布的方差近似', 2/(500))
print('kaiming均匀分布的方差leakyrelu', (2*((2*6/((1+0.3**2)*800))**0.5))**2/12)
print('kaiming均匀分布的方差近似leakyrelu', (2*((6/((1+0.3**2)*500))**0.5))**2/12)
print('kaiming正态分布的方差leakyrelu', 2*2/((1+0.3**2)*800))
print('kaiming正态分布的方差近似leakyrelu', 2/((1+0.3**2)*500))
[0, 1]均匀分布的均值与方差 0.5 0.08333333333333333
xavier均匀分布的方差 0.0025
kaiming均匀分布的方差 0.005
kaiming均匀分布的方差近似 0.004
xavier正态分布的方差 0.0025
kaiming正态分布的方差 0.005
kaiming正态分布的方差近似 0.004
kaiming均匀分布的方差leakyrelu 0.0045871559633027525
kaiming均匀分布的方差近似leakyrelu 0.0036697247706422016
kaiming正态分布的方差leakyrelu 0.004587155963302752
kaiming正态分布的方差近似leakyrelu 0.003669724770642202
Kaiming 中的 fan_in ,fan_out模式
kaiming_uniform_w = torch.nn.init.kaiming_uniform_(torch.empty(300, 500), a=0,mode='fan_in',nonlinearity='relu')
注意这一行,他的分母不是300,500的均值400,而是由一个参数mode控制,如果是fan_in 就是保证输入 分母是500,可以看一下这条
print('kaiming均匀分布的方差近似', (2*((6/(500))0.5))2/12)


