CNN-计算过程
材料准备
网络找了很多关于卷积神经网络的资料,综合来看,挑了一些比较有质量的材料汇总如下
1.鲁鹏老师的计算机视觉与深度学习
https://www.bilibili.com/video/BV1V54y1B7K3
2.邱锡鹏老师的蒲公英书
3.PRML关于卷积神经网络,不变性的章节(提供了一些不变性的总结和其他思路)
4.B站 权重初始化的意义及Xavier法与何恺明法的原理
https://www.bilibili.com/video/BV1ba411m72B
1.卷积网络的设计由来
- 1.全连接层忽略了像素之间的相关性,距离近的像素相关性自然强,远的自然弱
- 2.其实卷积的性质由全连接层也可以实现,毕竟神经网络有着强大的非线性拟合能力,但是问题在于全连接层的参数太多,训练起来太复杂
2.CNN的结构

一般的CNN都是如图上的结构
1.卷积层
2.Relu激活函数
3.卷积层
4.Relu激活函数
5.Pooing层(池化层,或者叫下采样 subsampling)
6.全连接层
7.softmax(或者其他分类器,如SVM)
为什么要重复的卷积呢?主要是扩大感受野
注意:卷积出来的数据(或者经过激活函数的),我们称之为特征响应图,这个会在解释CNN为什么能提取图片特征的博客中会专门讲解,本篇暂时不讲解
3.卷积的数学性质,数学公式
卷积的定义
上图
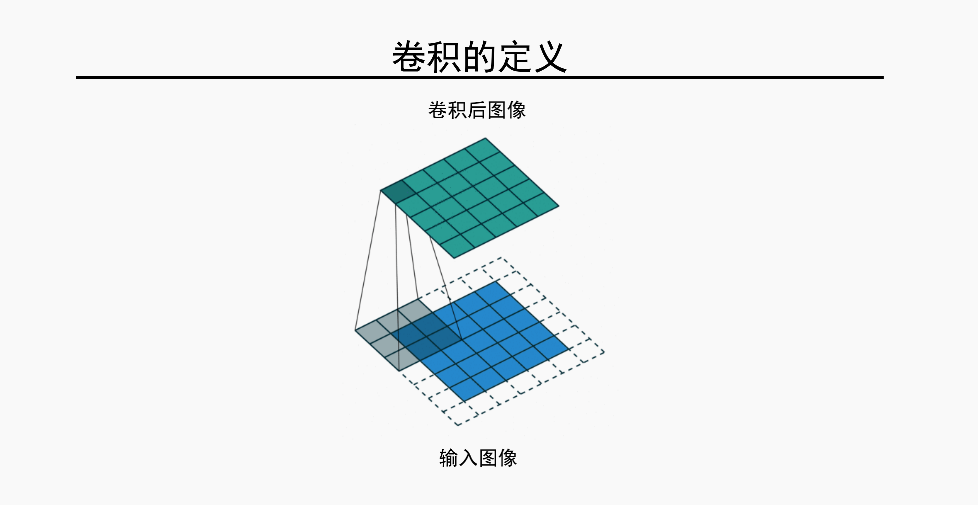
这个大家应该都懂,不谈了
正规的数据公式(邱锡鹏的蒲公英书中也有)

这里有一点说明,卷积操作其实需要将卷积核翻转180度后,再对对应位置的像素做点积操作,不翻转的卷积核点积操作叫互相关(蒲公英书)
然后一般卷积核都是对称的,所以这一点一般都是忽略的
信号中的卷积定义
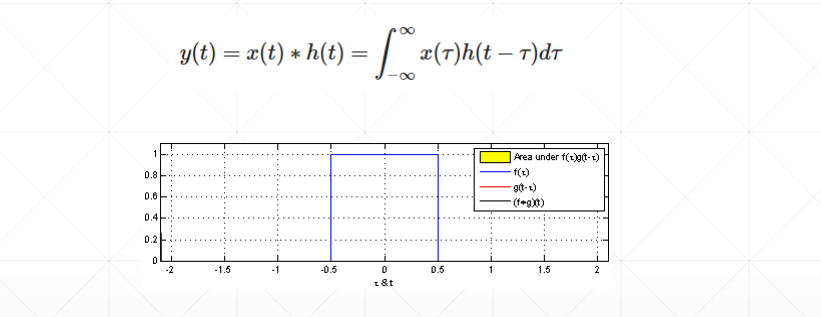
两个信号重叠的部分称之为卷积
这个公式给我们的启发就是如果你讲卷积视为一种特征提取函数(另外一篇博客会讲,比如说是能检测竖状,横状,斜状,圈状的函数),那么卷积后的数值大小即意味着这个像素点是否有状,横状,斜状,圈状的物体,或者说可能性有多大,可能性越大,那就越可能是某种形状的图片
PRML书的摘录
如果我们把每个单元想象成特征检测器,那么特征地图中的所有单元都检测了输⼊图像中的相同的模式,
但是位置不同。由于权值共享,这些单元的激活的计算等价于使⽤⼀个由权向量组成和“核”对图像像素的灰度值进⾏卷积。
如果输⼊图像发⽣平移,那么特征地图的激活也会发⽣等量的平移,否则就不发⽣改变。
这提供了神经⽹络输出对于输⼊图像的平移和变形的(近似)不变性的基础。
卷积的性质

卷积的麻烦地方-边界一般需要填充
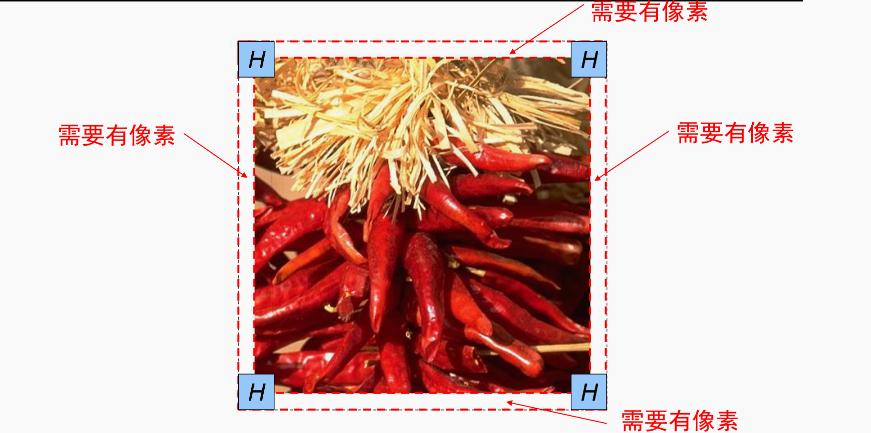
一般都填充零像素,其他诸如拉伸填充,镜像填充不扩展了
常用卷积核
单位脉冲核
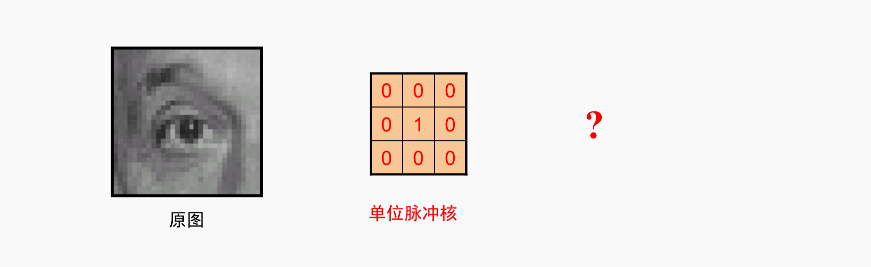
啥也没变,还是自己
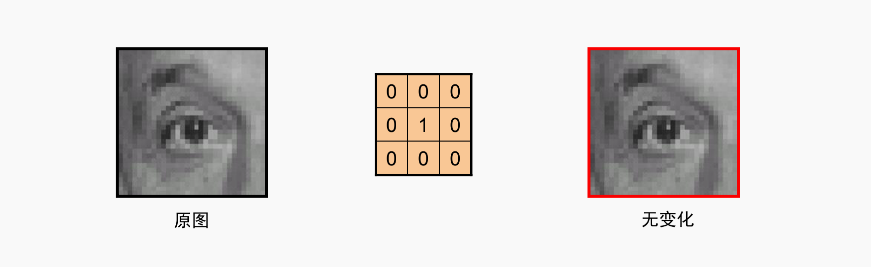
平移核
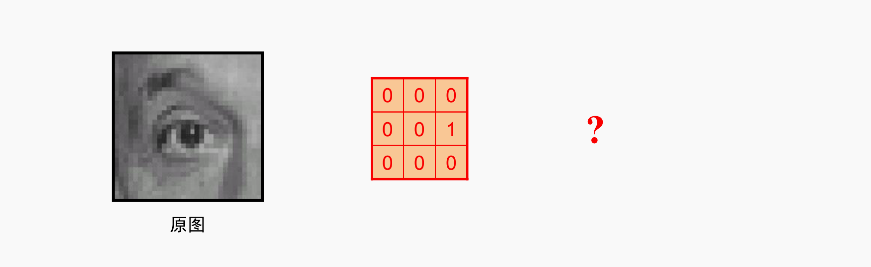
通过类似的核,可以往周围八个方向随意移动
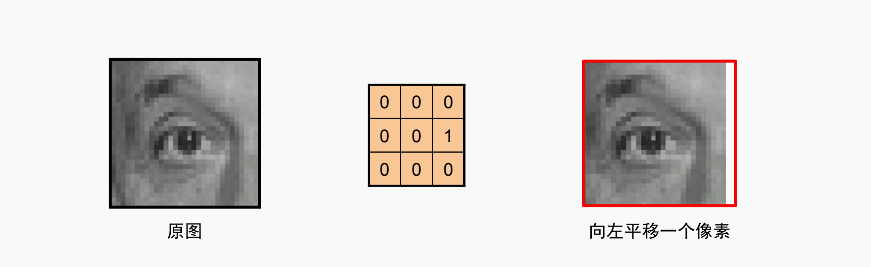
平滑,模糊,磨皮效果的核,平均核

把自己的像素值均摊给了周围的八个兄弟,是不是就是起了稀释的效果,图像上来说就是平滑,模糊了
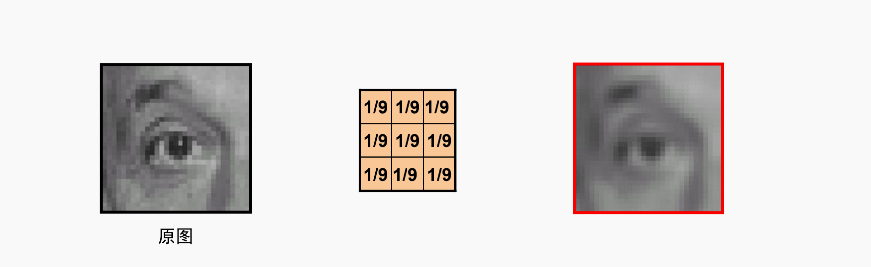
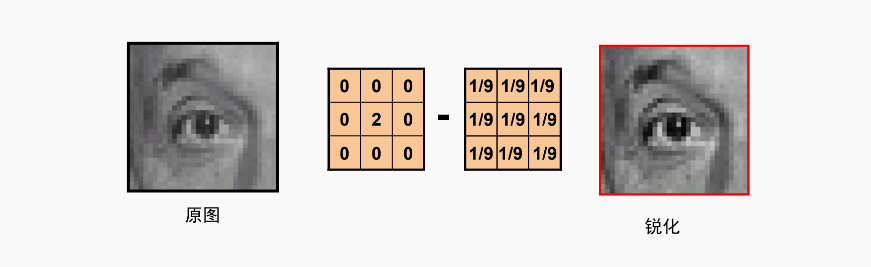
锐化核
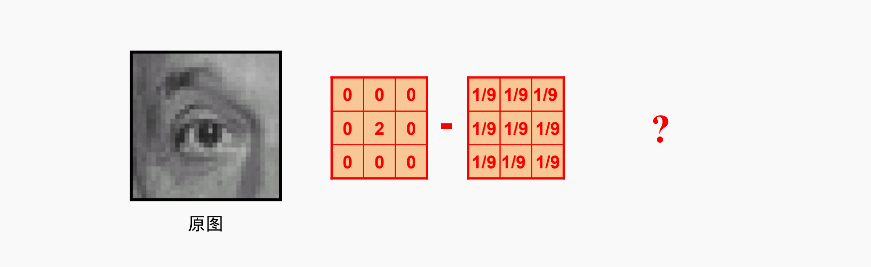
中间那个是减号
0 0 0 1/9 1/9 1/9
0 2 0 - 1/9 1/9 1/9
0 0 0 1/9 1/9 1/9
-1/9 -1/9 -1/9
-1/9 1+8/9 -1/9
-1/9 -1/9 -1/9
这个有难度了,这个是什么效果?锐化,为什么能起到锐化的效果?
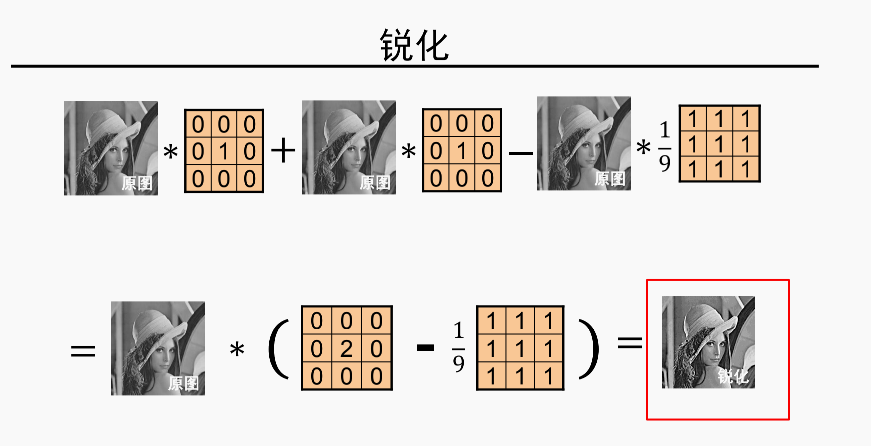
1.根据卷积的性质a(b-c) = ab -ac -这条放一边
2.看这个核计算,这个核计算的是什么? (原图(单位脉冲核)-平滑后的图) 是什么? 边缘图!!!! 我擦,原理都在这里,这么经典
0 0 0 1/9 1/9 1/9
0 1 0 - 1/9 1/9 1/9
0 0 0 1/9 1/9 1/9
3.再把边缘图加回原图,是不是就是把边缘更加锐化了!!!!! 我擦,真是恍然大悟!!!
0 0 0 0 0 0 1/9 1/9 1/9
0 1 0 + 0 1 0 - 1/9 1/9 1/9
0 0 0 0 0 0 1/9 1/9 1/9
4.再用上第一条,前面两个单位脉冲核变成了2倍关系
非常重要的核-高斯卷积核
用平均核没有考虑到离像素点近的核,显然权重应该更高的道理,用高斯核可以克服这一点
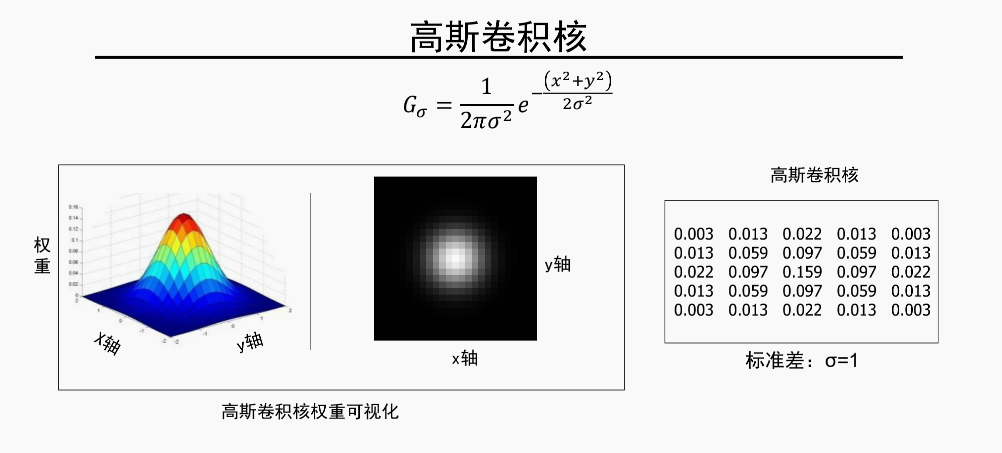

高斯卷积核两个重要的参数
1.核的尺寸大小
2.标准差
两个参数对高斯核的影响
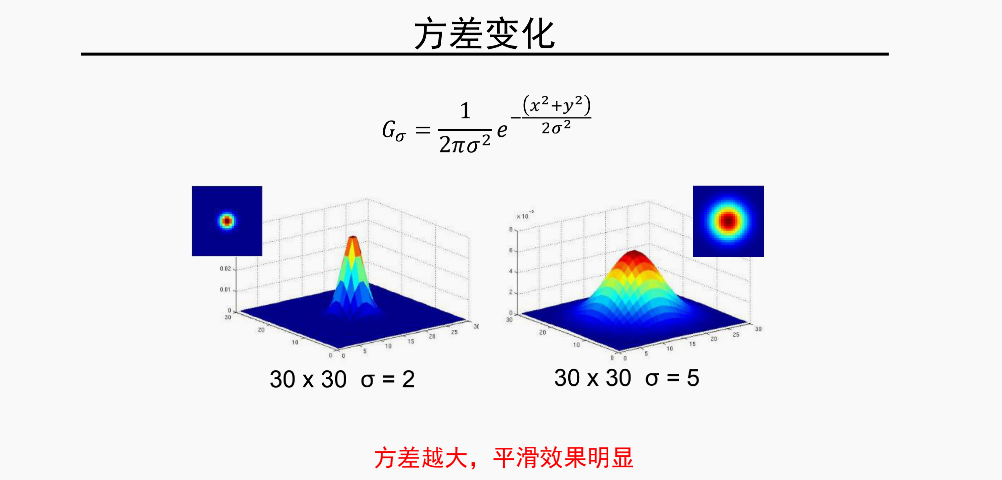
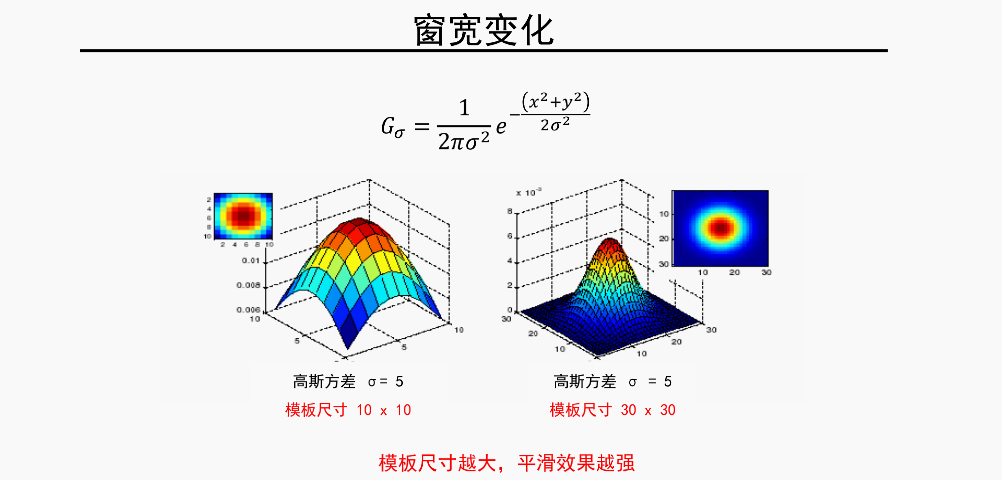
两个参数设置的经验法则
这样只要一个标准差参数,就够了

高斯核的性质
这里有两个很重要的性质要了解
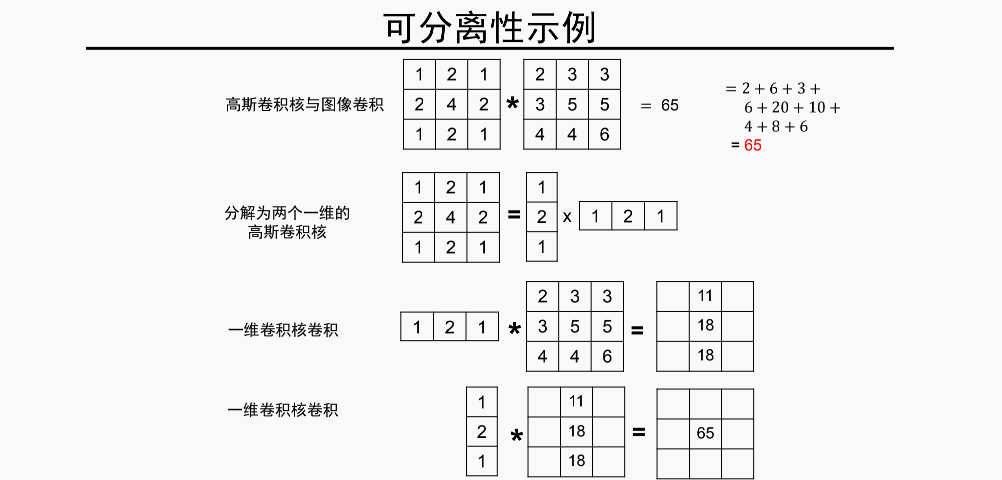
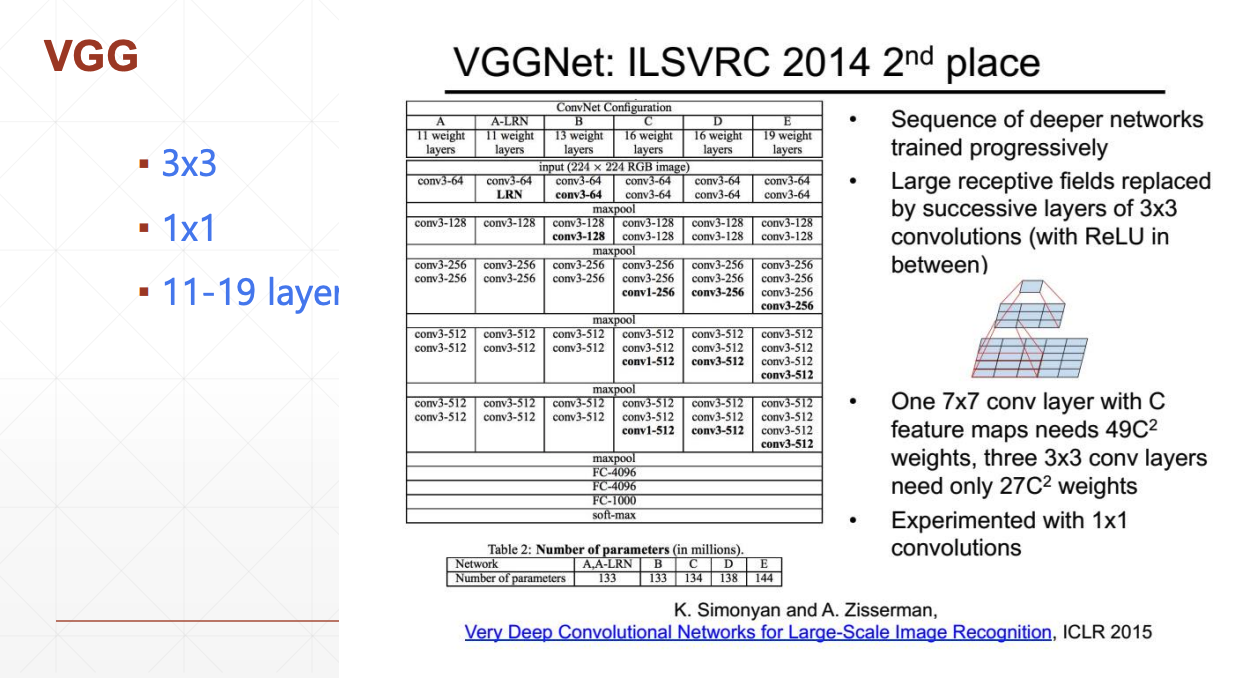
1.多个小方差卷积核等价于一个大方差卷积核相同的结果(所以一般,我们在CNN中用的是小卷积33的比较多,因为小的卷积计算量少,这一点在鲁鹏老师的视频中有证明,这里不展开了)
2.可分离称两个一维的高斯核的乘积,这点在GoolgeNet网络中被使用过,也就是说一个 33 的高斯卷积核可以分离出一个13和一个31的一维高斯卷积核,计算结果是一样的

4.池化(pooling)/下采样(subsampling)层
这个特征响应图就是卷积出来的数据



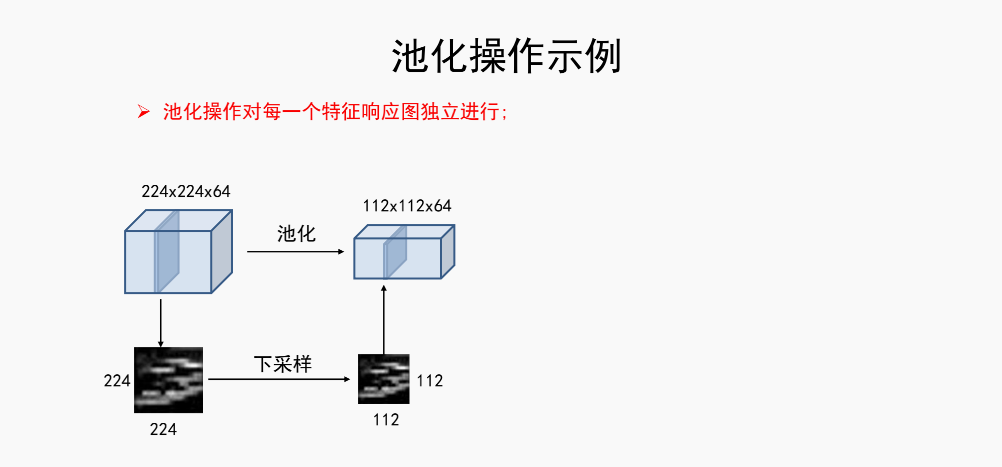
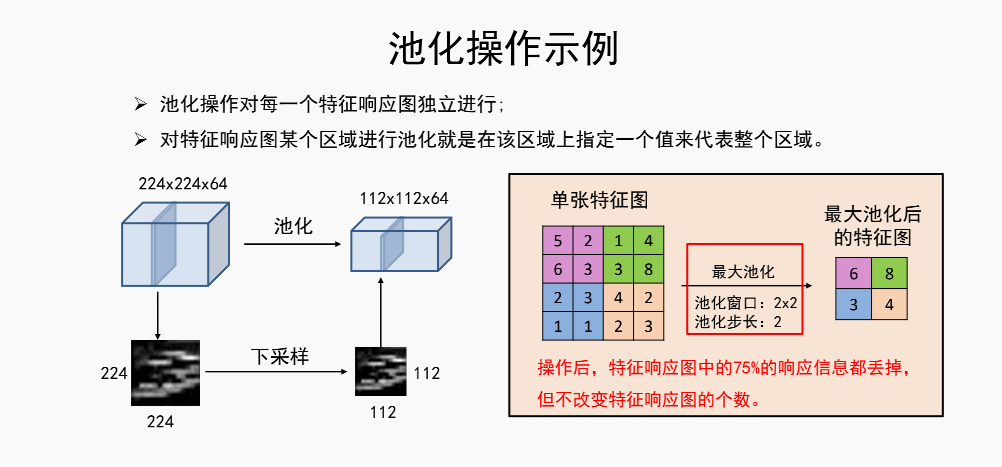
池化其实很简单,就是一个平均核或者是最大核
5.CNN的各层要素
相关的要素,核大小,激活函数
卷积核相关的参数很重要
相关的参数有
1.卷积核的尺寸-size
2.卷积核的深度-depth 一般3通道就是3深度
3.padding值 - 边缘填充
4.stride值 - 步长
参数之间的关系
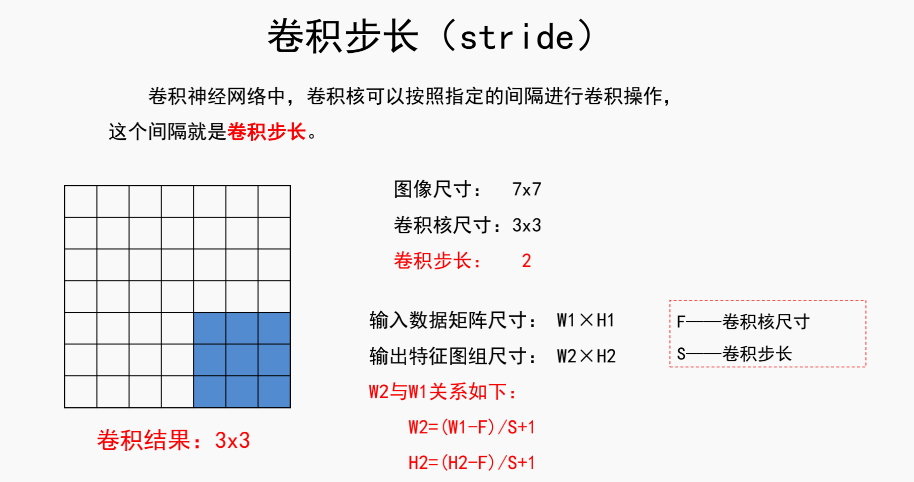
激活函数一般取Relu
6.CNN的计算过程
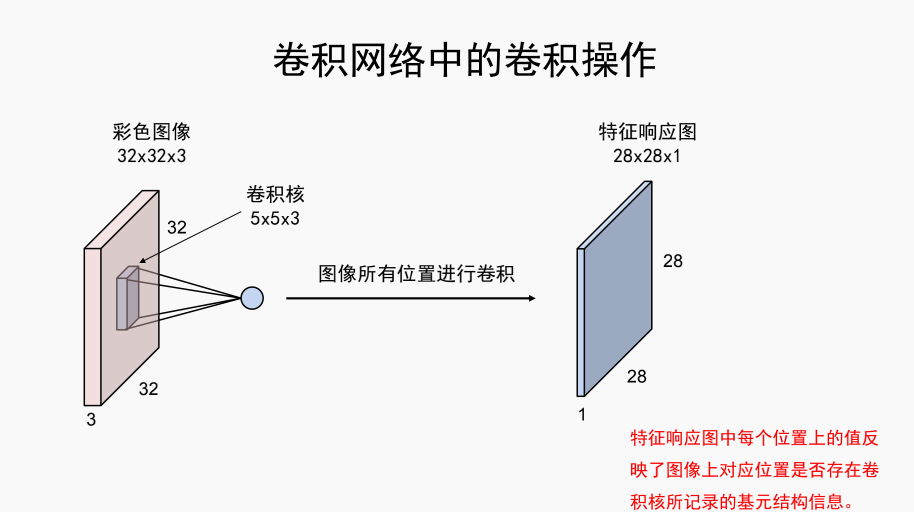
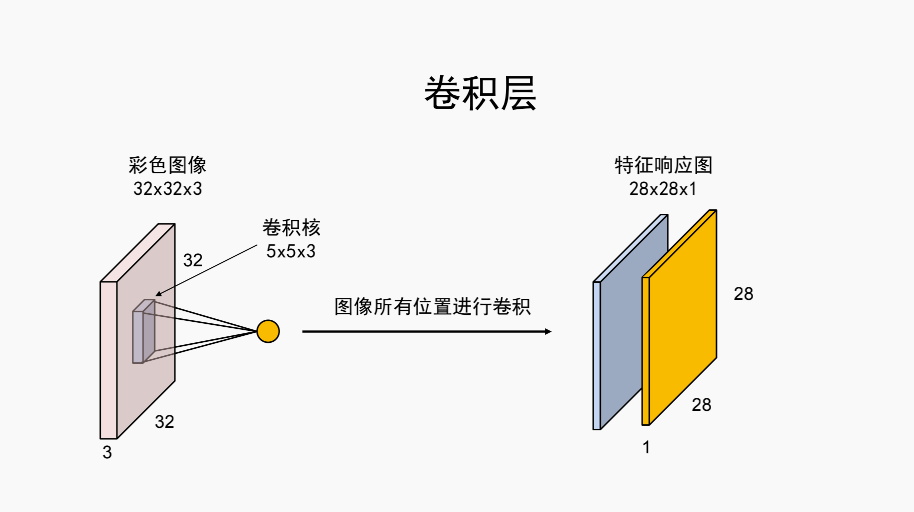
输入数据[batch_size,3,32,32] - batch_size 一般指训练的时候这个批次的训练数据大小,这里就是指这批次训练的时候有多少张图片,第二个参数是通道数
卷积核[6,3,5,5],共有6个卷积核,每个核3通道,都是5*5的大小
输出数据[batch_size,6,28,28]
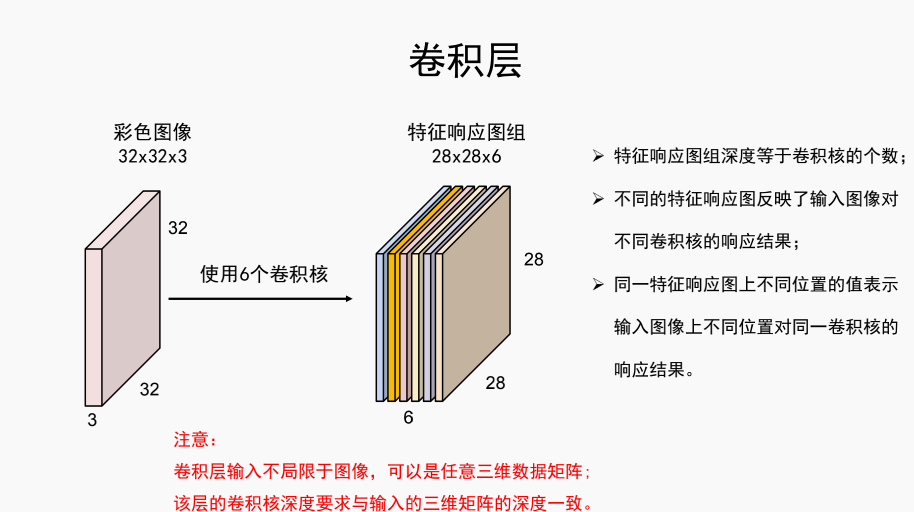
注意,若下面还有一层卷积
则下一层的卷积核应该为[10,6,5,5] ,10是我假设的数据,假设这一层用的是10个卷积核,关键是第二个参数,通道数(或者叫深度)是6,不是3,这个对应于第一层的卷积核的数量
这里有个问题,最后要做分类,我们势必希望一张照片有一个通道就可以了(比如灰度值通道),这样可以直接打平(flatten)成一个向量,丢到下面的全连接层,就容易做分类,3通道或者多通道没法变成向量处理,这个怎么办?
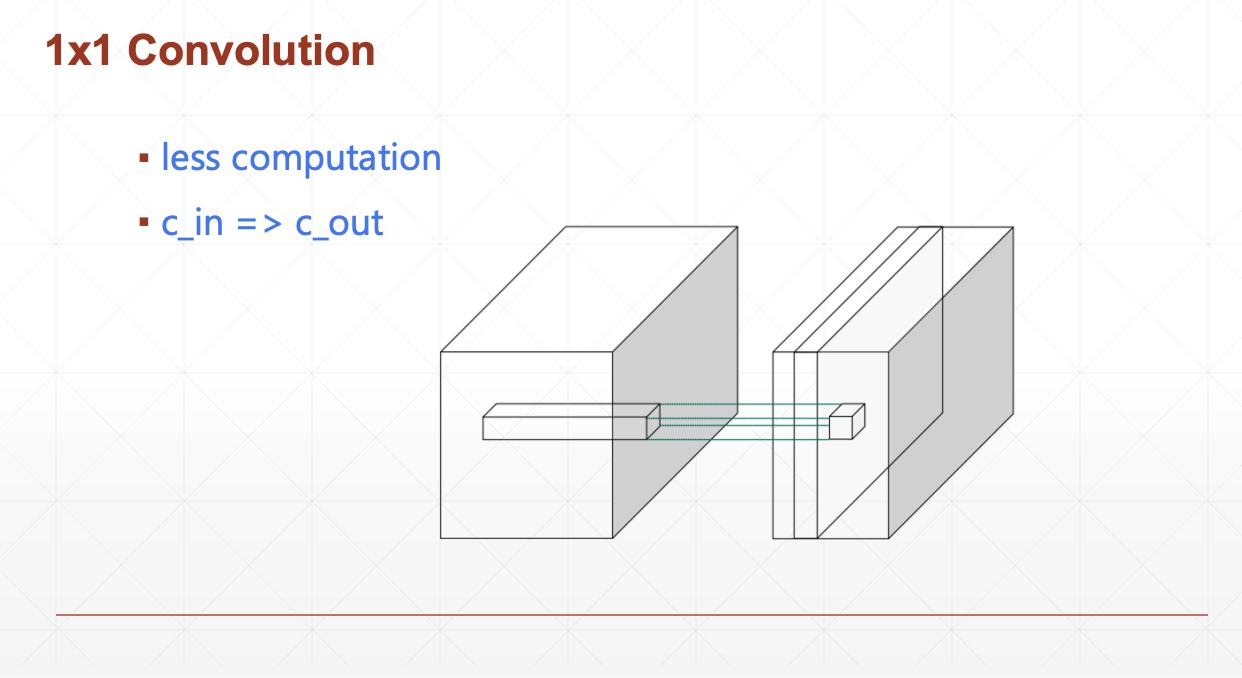
答:最后可以使用11的卷积核 [last_channels,1,11],last_channels是上一层的通道数(或者叫深度),这样就能保持原图像的数据基础上,降低深度
这样下一层的全连接层收到的参数只有 hw 也就是图片的尺寸大小这么多参数
如果不采用上面的操作,那么全连接将要接收到的参数有last_channelsh*w (维度3的向量矩阵也不是不能flatten)
VGG/GoogleNet中用到过1*1的卷积核
7.pytorch
点击查看代码
nn.Conv2d(3, 48, kernel_size=11, stride=4, padding=2)
# 第一个参数输入的通道数
# 第二个参数就是卷积核的数量


