概率图模型:原理与技术-3.3 图中的独立性,D-分离

d-分离

\(本节的目的是了解合适可以保证独立性条件(X\perp Y|Z)在于贝叶斯网络结构\mathcal(G)相关的分布中成立\)

直接连接

这个一看就是互相影响的，不可能独立

间接连接

考虑下面四种间接连接的情况





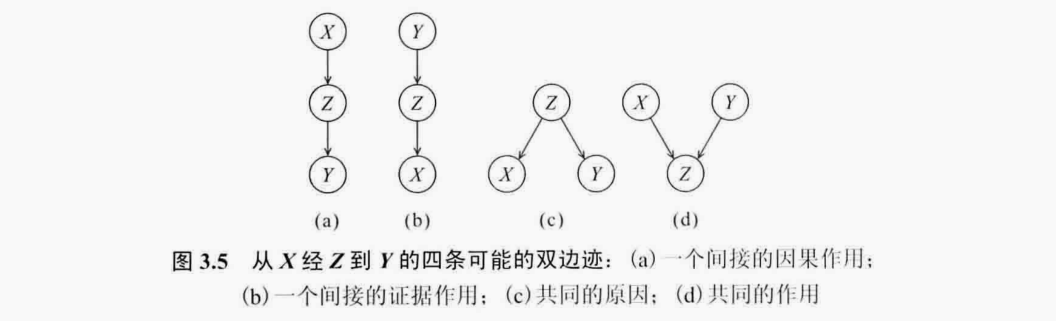
简单总结下就是
\(a,b,c三种情况是如果没有观察到Z。那么X，Y是相关的,有效的，可流通的\)
\(d这种情况是如果观察到了Z，那么X，Y是相关的,有效的，可流通的\)

有效迹与D-分离

这里说的很绕，但其实总结下来
1.什么是有效迹，对于上面abcd四种情况，不独立的，能相互影响的就是有效迹
这里注意一点，针对d这种情况，是Z观测到了反而是独立的，所以书上也有个例子

看下，DGI这条迹，因为G没有观测到，所以D,I是相互独立的，不流通的，DGIS这条也不是流通的
但当L观测到了，也就是G的后代被观测到了，那么DGI这条就是流通的
所以什么是有效迹？简而言之就是节点之间能流动的，相互影响的就是有效迹，主要搞懂上面abcd四种情况就懂了有效迹，因为也就这么四种情况
剩下D-分离就很简单了，不流动了，独立了就分离了