概率图模型:原理与技术-2.2图

基本概念

\(节点\mathcal{X}\)
\(边集\varepsilon\)
\(有向边:X_i \to X_j\)
\(无向边:X_i - X_j\)
\(X_i \rightleftharpoons X_j:这条边可以是有向的(任意方向),也可以是无向的\)
\(有向图\mathcal{G}\)
\(无向图\mathcal{H}\)

无向图

又定义了一些概念
\(父节点\)
\(子节点\)
\(邻节点\)
\(相邻\)
\(边界集\)
\(度(下面一张图)\)
\(入度\)
\(图的度\)

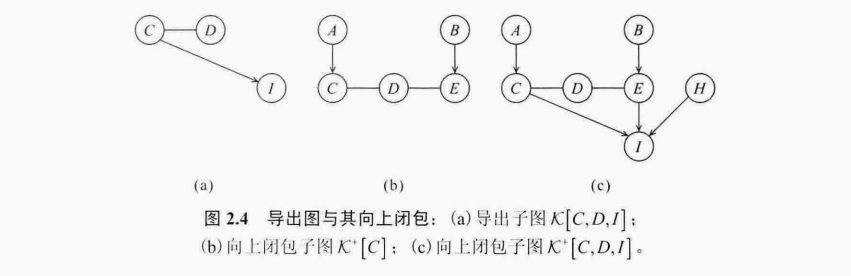
举例说明

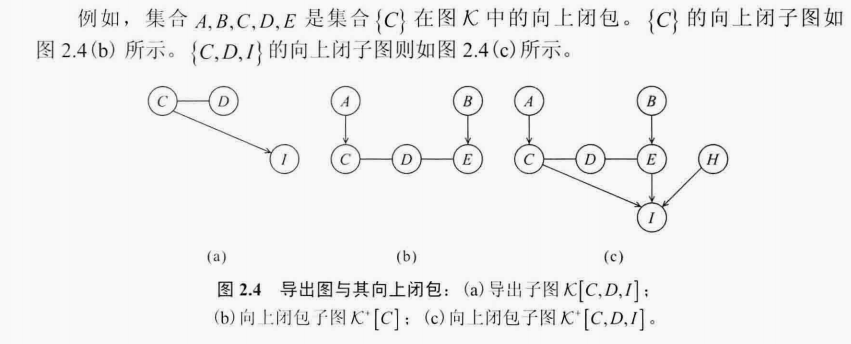
子图

导出子图

可以理解是图的一个子集，子集中的节点对应的边都要覆盖到

图要结合上面的2.3图一起看

团-重要概念

简单说就是子图中的任意两个节点都有边

向上闭子团

\(\color{red}{看不懂，太拗口，不知所云，暂时先放一放}\)

还是上面的例子

路径与迹

路径/有向路径

迹

迹的约束更小点，有线连着就行,不用管什么方向

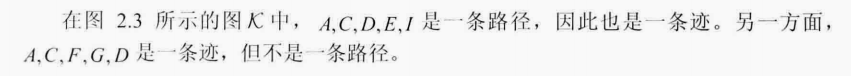
连通图

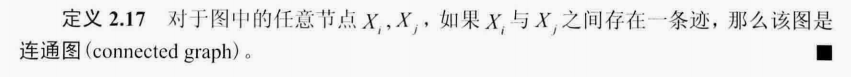
祖先/后代节点

拓扑序

\(\color{red}{妈呀，什么东西，战略性放一放}\)

圈

DAG/PDAG

链分支

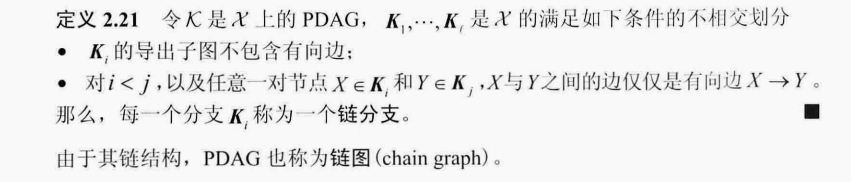
回到那个图2.3，有几个链分支?

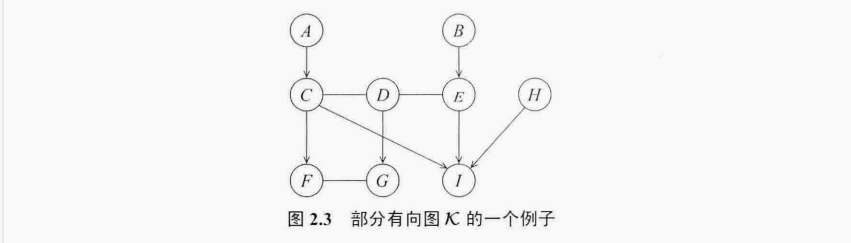
这里有点绕，注意链分支是图的一个划分，并且每个划分子集之间的连接都是有向边,而且是同一方向的有向边,比如(C,D,E)和(F,G)有两条同方向的有向边-这是第二点的说明
第一点的意思是划分子集中的边不能是有向边
总结一下就是可以先将有向边去除，看看通过无向边能不能形成孤立的子集，再看看这些子集之间的有向边是不是同一方向的,前面那一步好说，肯定可以操作，后面一步不一定所有的图划分出来都是同方向的边，所以这个大前提是必须是PDGA图

环

环与圈不是一个概念
环这个不要求是有向的，因为迹不要求一定是有向的
没有环的就是一颗树

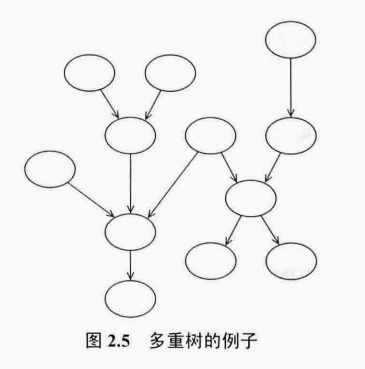
无环图是森林(直观上就是没有圈圈的),这时候有可能是多重树
每个节点至多一个父节点，那么就是森林，也就是一颗倒过来的自然形状的数,向下长的数
\(连通的概念:非空有向图 \mathcal{G}的任意两个节点之间都有一条路径存在，就称\mathcal{G} 是连通的。\)

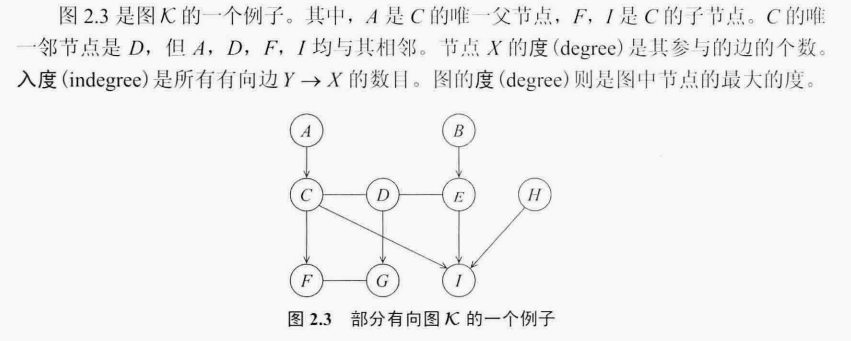
弦

\(图 \mathcal{G}中的一个圈 \mathcal{G}_L ，在L中不连贯的节点的边成为弦。\)