阻抗匹配
https://zhuanlan.zhihu.com/p/37700053
https://wenku.baidu.com/view/de1e5018f56527d3240c844769eae009591ba231.html
微波工程
1.用集总元件匹配(L网络)
电感电容匹配规律

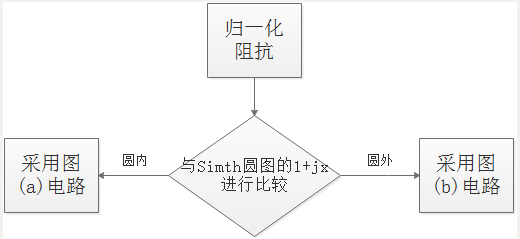
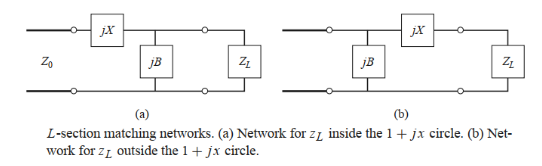
为了匹配任意负载到传输线,用两个电抗性元件组成L节。
例子
设计一个L节匹配网络,在频率500MHz,用以匹配\(Z_L\)=200-j100\(\Omega\)的RC串联负载到100\(\Omega\)传输线。
解1
- ①归一化负载\(z_L\)=2-j1,在1+jx圆内,采用上述图(a)匹配电路。由于从负载上看,第一个元件是并联电纳,通过负载画等SWR圆,且从负载过圆点的中心画一直线,这样就可以把负载阻抗转换成导纳,才能与该并联导纳相加。
- ②外加一个jb=j0.3电纳后,便能沿着等电纳圆移动到y=0.4+j0.5
- ③加上并联导纳之后再转换成阻抗z=1-j1.2。
- ④再串联电抗jx=j1.2即可实现匹配

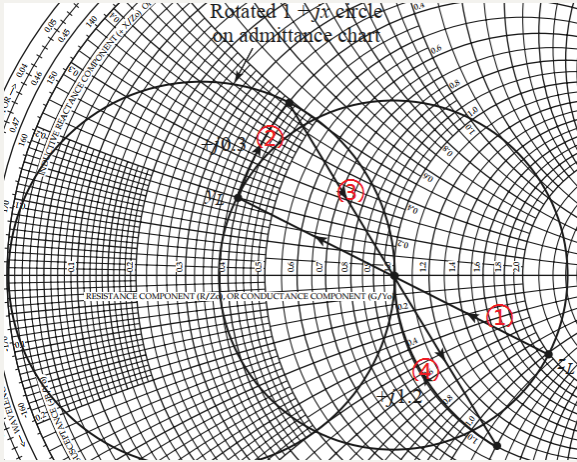
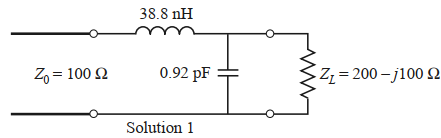
该匹配网络包括一个并联电容和一个串联电感
b=0.29,x=1.22
解2
- ①用一个jb=-j0.7并联电纳替代jb=j0.3,则移位到1+jx下半圆上的移动到点y=0.4-j0.5处
- ②加上并联导纳之后再转换成阻抗,加上x=-1.2的串联电抗
b=-0.69,x=1.22

短的传输线短截线可提供0~0.1pF的并联电容,在传输线中单缝隙或叉指形缝隙能够提供高达0.5pF作用的串联电容。
2.单短截线调谐
诸如微带线或带状线,开路短截线是容易制造的,因为不需要通过孔将基片与接地板相连。然而,对于同轴线或波导,通常用短路截线,因为开路短截线的横截面积对辐射来讲是足够大的(电学意义上)。
在单短截线调谐中,有两个可调参量:从负载到端截线的距离d和由并联或串联短截线提供的导纳或电抗。
对于并联短截线情况,基本思想是选择d,使其在距离负载d处看去导纳是\(Y_0+jB\)形式,然后,此端截线的电纳选择-jB就可以达到匹配。
对于串联短截线情况,同样选择距离d,使其在距离负载d处传输线看去电抗具有\(Z_0+jX\)形式,然后选择短截线的电抗为-jX以达到匹配条件。
2.1并联短截线
对于一个负载阻抗\(Z_L=60-j80\Omega\),设计两个单短截线(短路线)并联调谐网络,使这个负载与50\(\Omega\)匹配。
-
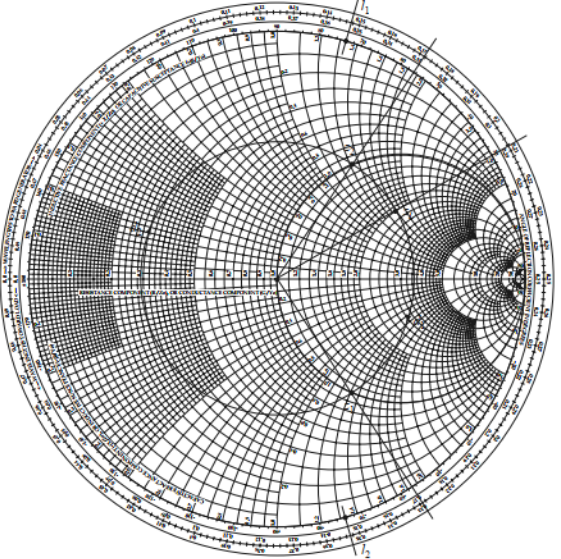
归一化负载阻抗\(z_L=1.2-j1.6\),然后做出对应的SWR圆,并转换到负载导纳\(y_L\)
-
接着把Smith圆图考虑成导纳圆图,注意SWR圆与1+jb圆相交两个点,用\(y_1和y_2\)表示,所以由负载到短截线的位置d由这两点的给出。
\[d_1=0.176-0.065=0.110\lambda \]\[d_2=0.325-0.065=0.260\lambda \]实际上,距离d有无限多个值,通常,我们希望匹配短截线尽可能靠近负载以提高匹配带宽,降低由于在短截线和负载间的传输线上可能发生的大驻波比引起的损耗。
-
这个两个相交点归一化导纳为
\[y_1=1+j1.47 \]\[y_2=1-j1.47 \] -
第一个调谐解需要一个电纳-j1.47的端接线。供给该电纳的短路短截线的长度可在Smith圆图找到,过程是以\(y=\infty\)(短路点)为起点,沿着圆外缘向着信号源方向旋转到-j1.47点,该短截线长度为
\[l_1=0.096\lambda ? \] -
同样,第二个调谐解短截线长度为
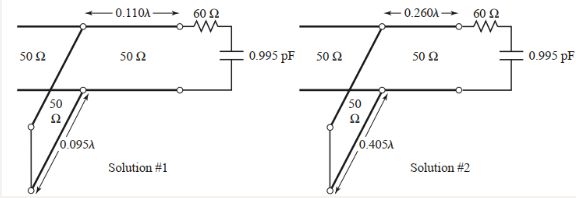
2.2串联短截线
用一个串联开路短截线,匹配负载阻抗\(Z_L=100+j80\)到50\(\Omega\)的传输线上。
- 画出Smith圆图上的归一化阻抗\(z_l=2+j1.6\),并画出SWR圆
- SWR圆与1+jx有两个交点\(z_1,z_2\),其中\(d_1\)
-
交点处的归一化阻抗为
\[z_1=1-j1.33 \]\[z_2=1+j1.33 \] -
以\(z=\infty\)为起点,短截线长度为
3.多节变换器
四分之一波长变换器提供了任意实数负载阻抗与任意传输线阻抗匹配的方法。而当需要带宽大于当个四分之一波长节所能提供的带宽时,可用多节变换器。
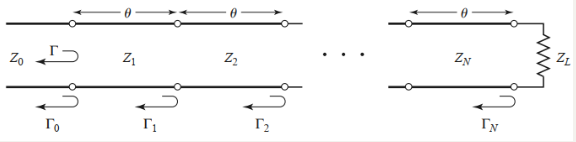
- 二项式多节匹配变换器(最平坦响应)
- 切比雪夫多节匹配变换器(等波纹响应),与二项式变换器相比,切比雪夫变换器是以通带内的波纹为代价而得到的最佳带宽。因此对于给定节数切比雪夫变换器的带宽较好。
4.渐变传输线
当分立的节数N增加时,各节之间的特征阻抗阶跃变化随之变小,所以在无限多个节的极限情况下,可以近似为一段连续渐变的传输线。

4.1指数渐变
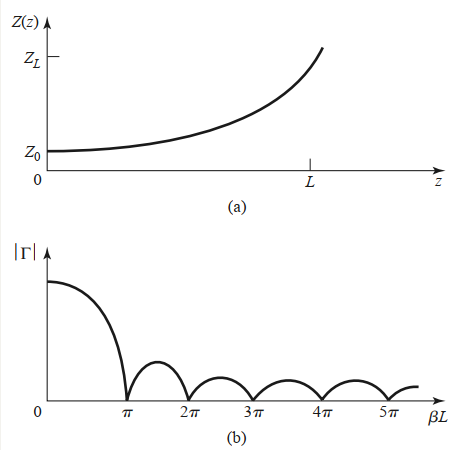
\(|\Gamma|\)的峰值随着长度的增加而减小,为了降低在低频处的失配,长度应该大于\(\lambda(\beta l>\pi)\)
4.2三角形渐变

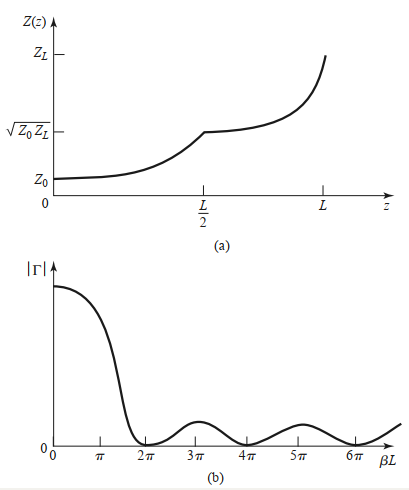
对于\(\beta l>2\pi\),三角形渐变的峰值低于相应指数情形的峰值,但是,三角形渐变的第一个零点发生在\(\beta l=2\pi\),而指数渐变发生在\(\beta l=\pi\)
4.3 Klopfenstein渐变
对于给定的渐变长度,反射系数在整个通带是最小的



 浙公网安备 33010602011771号
浙公网安备 33010602011771号