Naive Bayes 朴素贝叶斯

高斯型 ，适合特征值连续值的情况，如鸢尾花的花瓣和花萼的长宽

  • 对于同一个input ，在某个正态分布上所在的区间更接近置信区间中心，对应的Y值大 ，说明它更像是这个label上的某一个样本

  • Geogebra 模拟
    label0：

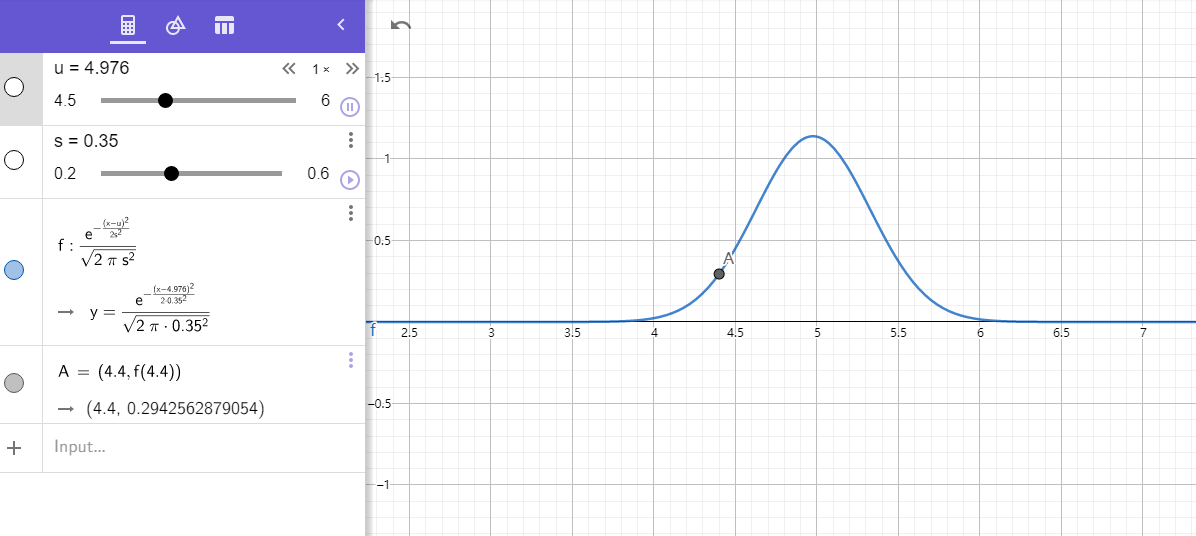
    label1：

  • result summary：

label0:
meanVal :  array([4.96571429, 3.38857143, 1.47428571, 0.23714286])
stdevVal : array([0.35370921, 0.36077015, 0.16620617, 0.10713333])
0 [0.3139061  0.96461384 1.38513086 3.50658634] 1.4707152132084353

label1:
meanVal:  array([5.90285714, 2.71142857, 4.21142857, 1.29714286])
stdevVal: array([0.52180221, 0.28562856, 0.49267284, 0.19196088])
1 [1.20819778e-02 3.23420084e-01 2.11449510e-08 1.67604215e-07] 1.3848305491176349e-17
  1. 黄海广副教授 ,温州大学 ，对NB算法给出了很简单易行的代码,这里用待用pandas.dataframe 简化
  2. 概括起来，统计每种类型 每个特性的mean, std ， 对于待预测样本的每个特性计算高斯概率 ， 结果是每个特性的概率相乘
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math
def gaussian_probability( x, mean, stdev):
    exponent = math.exp(-(math.pow(x - mean, 2) /
                            (2 * math.pow(stdev, 2))))
    return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent
# data
X,y = load_iris(return_X_y=True)
X=X[:100,:]
y=y[:100]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)


df_train = pd.DataFrame(X_train, columns=['sepal length', 'sepal width', 'petal length', 'petal width'])
df_train['label'] = y_train
#fit 
groupLabel= df_train.groupby(by = 'label' ).size()
#统计每种类型 每个特性的mean, std , 

inputVal=np.array([4.4,  3.2,  1.3,  0.2])
for idx, targetLabel in enumerate(groupLabel.index):
    meanVal= df_train[ df_train['label'] == targetLabel].mean().values[:-1]
    stdevVal= df_train[ df_train['label'] == targetLabel].std(ddof=0).values[:-1]
#计算概率 对于特定的输入 求解它的特性与训练样本构成的高斯概率
    gaussian_probability= np.exp(-  0.5* (inputVal-meanVal)**2 / stdevVal**2  ) / np.sqrt( 2*np.pi   ) / stdevVal
    probabilities=1
    for prob in gaussian_probability: 
        probabilities  = probabilities* prob

    print(targetLabel,gaussian_probability, probabilities )

伯努利型 ，适合特征值有两个（如 0 1） 的情况，如mnist图片二值化后对应的0 1

  • 参考 https://www.cnblogs.com/wj-1314/p/10560870.html

  • 离散型对应的 公式 如下
    概括起来，
    验证概率： 统计每种label的比例
    条件概率：第I个取值的条件概率即 前Label中维度J中的I个数 / 当前label的样本数

  • 参考作者的代码，手写数字的准确度有83%
    贴上完整测试代码， 数据集可以直接使用from keras.datasets import mnist ，或作者的GitHub

#_*_coding:utf-8_*_
 
import pandas as pd
import numpy as np
import cv2
import time
 
from sklearn.model_selection import train_test_split
from sklearn.metrics  import accuracy_score
 
# 获取数据
def load_data():
    # 读取csv数据
    raw_data = pd.read_csv('train.csv', header=0)
    data = raw_data.values
    features = data[::, 1::]
    labels = data[::, 0]
    # 避免过拟合，采用交叉验证，随机选取33%数据作为测试集，剩余为训练集
    train_X, test_X, train_y, test_y = train_test_split(features, labels, test_size=0.33, random_state=0)
    return train_X, test_X, train_y, test_y
 
# 二值化处理
def binaryzation(img):
    # 类型转化成Numpy中的uint8型
    cv_img = img.astype(np.uint8)
    # 大于50的值赋值为0，不然赋值为1
    cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img)
    return cv_img
 
# 训练，计算出先验概率和条件概率
def Train(trainset, train_labels):
    # 先验概率
    prior_probability = np.zeros(class_num)
    # 条件概率
    conditional_probability = np.zeros((class_num, feature_len, 2))
 
    # 计算
    for i in range(len(train_labels)):
        # 图片二值化，让每一个特征都只有0， 1 两种取值 ,0 是目标区域
        img = binaryzation(trainset[i])
        label = train_labels[i]
        #先验证概率： 统计每种label的比例
        prior_probability[label] += 1
        for j in range(feature_len):
            conditional_probability[label][j][img[j]] += 1
 
    # 将条件概率归到 [1, 10001]
    for i in range(class_num):
        for j in range(feature_len):
            # 经过二值化后图像只有0， 1 两种取值
            pix_0 = conditional_probability[i][j][0]
            pix_1 = conditional_probability[i][j][1]
            # 计算0， 1像素点对应的条件概率
            probability_0 = (float(pix_0)/float(pix_0 + pix_1))*10000 + 1
            probability_1 = (float(pix_1)/float(pix_0 + pix_1))*10000 + 1
 #条件概率：第I个取值的条件概率即      当前Label中维度J中的I个数 /  当前label的样本数
            conditional_probability[i][j][0] = probability_0
            conditional_probability[i][j][1] = probability_1
 
    return prior_probability, conditional_probability
 
# 计算概率
def calculate_probability(img, label):
    probability = int(prior_probability[label])
    for j in range(feature_len):
        probability *= int(conditional_probability[label][j][img[j]])
    return probability
 
# 预测
def Predict(testset, prior_probability, conditional_probability):
    predict = []
    # 对于每个输入的X，将后验概率最大的类作为X的类输出
    for img in testset:
        # 图像二值化
        img = binaryzation(img)
 
        max_label = 0
        max_probability = calculate_probability(img, 0)
        for j in range(1, class_num):
            probability = calculate_probability(img, j)
            if max_probability < probability:
                max_label = j
                max_probability = probability
        predict.append(max_label)
    return np.array(predict)
 
 
# MNIST数据集有10种labels，分别为“0，1,2，3,4,5,6,7,8,9
class_num = 10
feature_len = 784
 
if __name__ == '__main__':
    time_1 = time.time()
    train_X, test_X, train_y, test_y = load_data()
    prior_probability, conditional_probability = Train(train_X, train_y)
    test_predict = Predict(test_X, prior_probability, conditional_probability)
    score = accuracy_score(test_y, test_predict)
    print(score)
posted @ 2021-04-26 08:59  boyang987  阅读(87)  评论(0)  编辑  收藏  举报