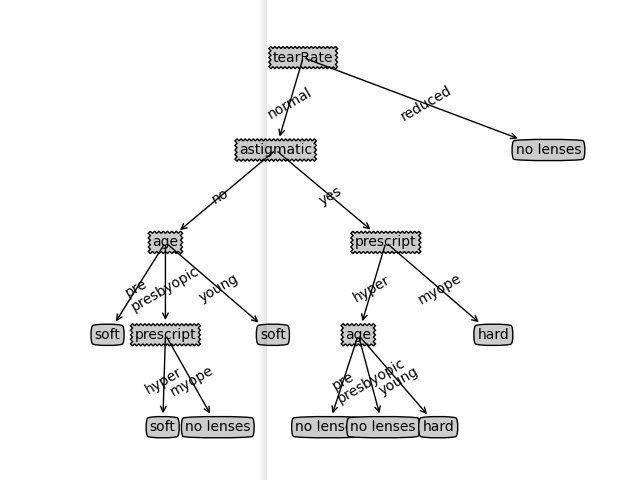
决策树 Decision Tree
参考
https://www.cnblogs.com/wj-1314/p/9428494.html
数据集D的经验熵H(D)
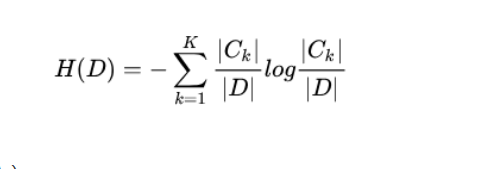
特征A对数据集D的经验条件H(D|A)
条件熵H(D|A)表示在已知随机变量A的条件下随机变量Y的不确定性

信息增益 (熵能减少的程度)
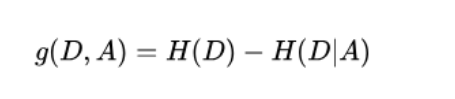
举例说明计算过程
通过声音粗细和头发长短判断男女,如下图
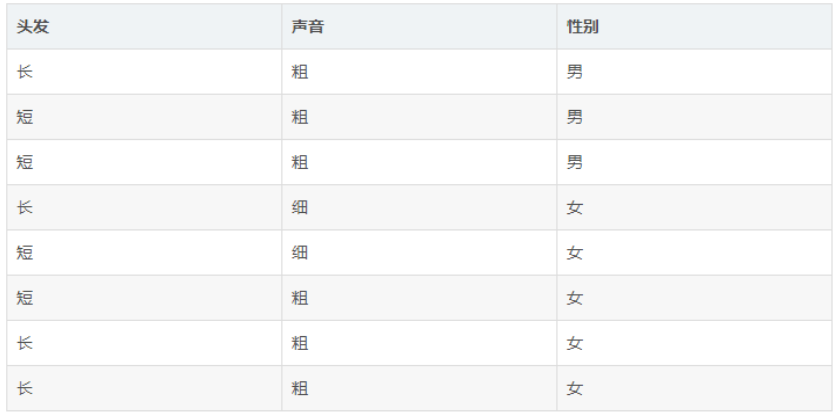
- 先选择特性 “头发” 来作为决策树的一个节点
H(D) = -3/8 * log(3/8) - 5/8 * log(5/8) = 0.9544
H(Di | 长头发) = -1/4 * log(1/4) - 3/4 log(3/4) = 0.8112
H(Di | 短头发) = -2/4 * log(2/4) - 2/4 log(2/4) = 1
H(D | 头发) = 长头发样本比例 * H(Di | 长头发) + 短头发样本比例 * H(Di | 短头发)= 4/8 * 0.8112 + 4/8 * 1=0.9056
先选择特性 “头发” 的信息增益 =H(D) - H(D | 头发) =0.0488 - 先选择特性 “声音” 来作为决策树的一个节点
H(D) = -3/8 * log(3/8) - 5/8 * log(5/8) = 0.9544
H(Di | 粗声音) = -3/6 * log(3/6) - 3/6 * log(3/6) = 1
H(Di | 细声音) = -2/2 * log(2/2) - 0/2 = 0
H(D | 声音)= 粗声音样本比例 * H(Di| 粗声音) +细声音样本比例 * * H(Di | 细声音) = 6/8 * 1 + 0 = 0.75
先选择特性 “声音” 的信息增益 = H(D) - H(D | 声音) = 0.2044
3.总结,按照信息增益的大小,选择信息增益大的声音作为决策树的一个节点,区分样本的能力更强
采用Python 的dictionary作为树形数据结构表示 构造决策树
- 参考wj-1314 , https://www.cnblogs.com/wj-1314/p/10268650.html
- 做个简单的例子,理解DT Tree与binary tree的创建实际相同
中序遍历与前序的结果创建二叉树
- 先贴上代码
# InLst= [4,2,1,5,3,6]
# PreLst= [1,2,4,3,5,6]
def CreateBinaryTree(InLst,PreLst):
#前序遍历的第一个节点是中间节点A
#终止条件
assert(len(InLst)== len(PreLst))
if len(InLst)< 1: return 'leaf'
A= PreLst[0]
leftPart= InLst.index(A)
myTree= {A:{}}
myTree[A]['left'] = CreateBinaryTree(InLst[:leftPart], PreLst[1:leftPart+1] )
myTree[A]['right'] = CreateBinaryTree(InLst[leftPart+1:],PreLst[leftPart+1:])
return myTree
- 树结构截图
ps: Leetcode 树结构可视化
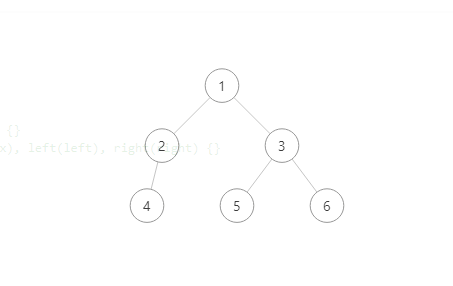
- 调用createPlot 创建的
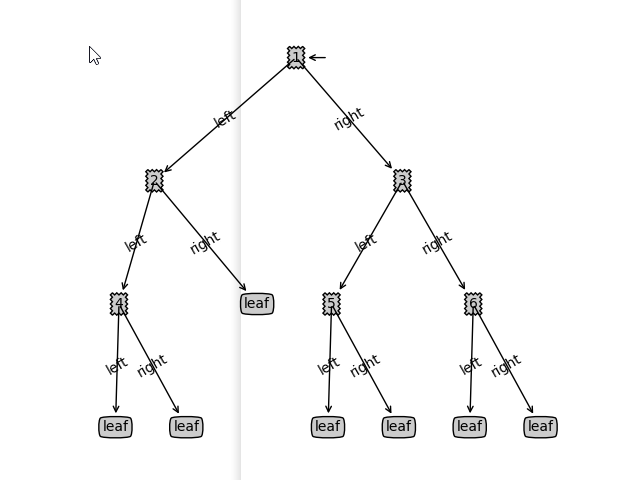
- 搞清楚createPlot内部制图的过程
-
确定是采用前序遍历 (递归) ,用Geogebra 看下每个节点出现的先后顺序,请对比上图来看
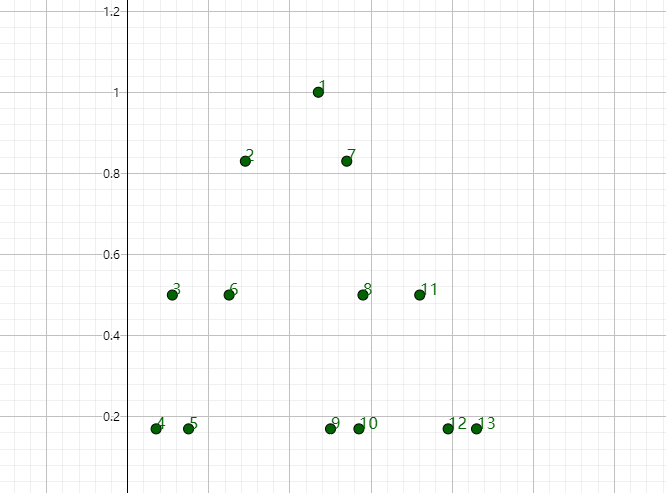
-
ps: Geogebra 脚本

- 关于 树的递归,
- 全局变量法,即返回值用全局变量或类的成员变量收集
- 函数返回值法,即在函数返回值中完成回溯,难度高些
- getNumLeafs的全局变量法代码
def getNumLeafs(myTree):
#终止条件
if( type(myTree).__name__ != 'dict' ):
getNumLeafs.LeafsCnt +=1
return
#当前树层的所有可以选的元素列表
for key in myTree.keys():
getNumLeafs(myTree[key])
def callit(myTree):
getNumLeafs.LeafsCnt=0
getNumLeafs(myTree)
return getNumLeafs.LeafsCnt
- getNumLeafs的函数返回值法,基于全局法写这个代码要简单很多
#中间 用Dictionary 实现Tree 并遍历
def getNumLeafs(myTree):
#终止条件
if type(myTree).__name__ != 'dict' :
return 1
firstRow= list(myTree.keys()) #node
secondRow= myTree[firstRow[0]] # left ,right ...
res=0
for key in secondRow.keys():
res += getNumLeafs(secondRow[key])
return res
- getTreeDepth的全局变量法代码
def getTreeDepth(myTree, pathLen):
#终止条件
if( type(myTree).__name__ != 'dict' ):
#print(pathLen)
if getTreeDepth.Depths< pathLen : getTreeDepth.Depths= pathLen;
return
firstRow = list(myTree.keys()) #node
secondRow = myTree[firstRow[0]] #分叉,left right...
#与求叶子节点个数的函数 getNumLeafs 参考看
#当前树层的所有可以选的元素列表
for key in secondRow.keys():
getTreeDepth(secondRow[key],pathLen+1 )
def callit(myTree):
getTreeDepth.Depths=0
getTreeDepth(myTree,0)
return getTreeDepth.Depths;
- getTreeDepth的函数返回值法
def getTreeDepth(myTree):
#终止条件
if type(myTree).__name__ != 'dict' :
return 0
firstRow = list(myTree.keys()) #node
secondRow = myTree[firstRow[0]] #分叉,left right...
#与求叶子节点个数的函数 getNumLeafs 参考看
#当前树层的所有可以选的元素列表
Depths=0
for key in secondRow.keys():
t= 1 + getTreeDepth(secondRow[key] )
if t> Depths : Depths = t
return Depths
- 使用pandas.DataFrame() 替代原作者wj-1314中的list,用来直接读CSV,处理属性分组情况,代码更加简洁
#type(dataSet): pd.DataFrame
def createTree(dataSet):
#递归终止条件1
#类别完全相同则停止继续划分
featValues= dataSet.groupby(by = 'label').size()
if featValues.size ==1: return featValues.index[0]
#递归终止条件2
#当所有特性都选择完时候
if dataSet.columns.size == 1: return featValues.index[featValues.values.argmax()]
#选择信息增益最大的特性
#1. 对每个特性都做选择 算出比列
#2. 在选择的Di中求 香农熵
#3. H(D|A ) = 1. * 2.
#4. gain= H(D) - H(D|A)
#H_D = -1.0 * np.sum( (featValues.values/featValues.values.sum()) * np.log2(featValues.values/featValues.values.sum()))
HDAVal= np.zeros((dataSet.columns[:-1].size,))
for col,featName in enumerate(dataSet.columns[:-1] ) :
featValues2 = dataSet.groupby(by = featName ).size()
ratio= featValues2.values/featValues2.values.sum()
H_D_A= np.zeros_like(ratio)
for row, DiName in enumerate( featValues2.index):
Di = dataSet[ dataSet[featName] == DiName ]
featValues3= Di.groupby(by = 'label').size()
H_D_A[row] = -1.0 * np.sum( featValues3.values/ featValues3.values.sum() * np.log2(featValues3.values/featValues3.values.sum()) )
HDAVal[col]= np.sum(H_D_A * ratio )
bestFeatLabel= dataSet.columns[:-1][HDAVal.argmin()]
#tree的结构 当前选择的特性作为Key,剩下元素是子节点
myTree = {bestFeatLabel:{}}
# 当前特性的属性值
featValues4= dataSet.groupby(by = bestFeatLabel ).size()
for value in featValues4.index:
#选择特性A 为value的样本 ,输出的DataFrame不包含A这一列
subDataSet = dataSet[dataSet[bestFeatLabel ] == value ] .drop(columns=bestFeatLabel )
myTree[bestFeatLabel][value] = createTree(subDataSet)
#这里可以理解为二叉树中的后序遍历 插入新节点
return myTree
- 值得一说的是 pickle (泡菜) ,可以帮助持久化任何Python object
- 完整的预测是否适合佩戴隐形眼镜 的代码
# _*_coding:utf-8_*_
import operator
from math import log
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#LeafsCnt=0
# 使用pickle模块存储决策树
def storeTree(inputTree,filename):
import pickle
fw =open(filename,'wb')
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename,'rb')
return pickle.load(fr)
#type(dataSet): pd.DataFrame
def createTree(dataSet):
#递归终止条件1
#类别完全相同则停止继续划分
featValues= dataSet.groupby(by = 'label').size()
if featValues.size ==1: return featValues.index[0]
#递归终止条件2
#当所有特性都选择完时候
if dataSet.columns.size == 1: return featValues.index[featValues.values.argmax()]
#选择信息增益最大的特性
#1. 对每个特性都做选择 算出比列
#2. 在选择的Di中求 香农熵
#3. H(D|A ) = 1. * 2.
#4. gain= H(D) - H(D|A)
#H_D = -1.0 * np.sum( (featValues.values/featValues.values.sum()) * np.log2(featValues.values/featValues.values.sum()))
HDAVal= np.zeros((dataSet.columns[:-1].size,))
for col,featName in enumerate(dataSet.columns[:-1] ) :
featValues2 = dataSet.groupby(by = featName ).size()
ratio= featValues2.values/featValues2.values.sum()
H_D_A= np.zeros_like(ratio)
for row, DiName in enumerate( featValues2.index):
Di = dataSet[ dataSet[featName] == DiName ]
featValues3= Di.groupby(by = 'label').size()
H_D_A[row] = -1.0 * np.sum( featValues3.values/ featValues3.values.sum() * np.log2(featValues3.values/featValues3.values.sum()) )
HDAVal[col]= np.sum(H_D_A * ratio )
bestFeatLabel= dataSet.columns[:-1][HDAVal.argmin()]
#tree的结构 当前选择的特性作为Key,剩下元素是子节点
myTree = {bestFeatLabel:{}}
# 当前特性的属性值
featValues4= dataSet.groupby(by = bestFeatLabel ).size()
for value in featValues4.index:
#选择特性A 为value的样本 ,输出的DataFrame不包含A这一列
subDataSet = dataSet[dataSet[bestFeatLabel ] == value ] .drop(columns=bestFeatLabel )
myTree[bestFeatLabel][value] = createTree(subDataSet)
#这里可以理解为二叉树中的后序遍历 插入新节点
return myTree
#中间 用Dictionary 实现Tree 并遍历
def getNumLeafs(myTree):
#终止条件
if type(myTree).__name__ != 'dict' :
return 1
firstRow= list(myTree.keys()) #node
secondRow= myTree[firstRow[0]] # left ,right ...
res=0
for key in secondRow.keys():
res += getNumLeafs(secondRow[key])
return res
#函数返回值法
def getTreeDepth(myTree):
#终止条件
if type(myTree).__name__ != 'dict' :
return 0
firstRow = list(myTree.keys()) #node
secondRow = myTree[firstRow[0]] #分叉,left right...
#与求叶子节点个数的函数 getNumLeafs 参考看
#当前树层的所有可以选的元素列表
Depths=0
for key in secondRow.keys():
t= 1 + getTreeDepth(secondRow[key] )
if t> Depths : Depths = t
return Depths
# 定义文本框和箭头格式(树节点格式的常量)
decisionNode = dict(boxstyle='sawtooth',fc='0.8')
leafNode = dict(boxstyle='round4',fc='0.8')
arrows_args = dict(arrowstyle='<-')
#https://blog.csdn.net/qq_30638831/article/details/79938967
# 绘制带箭头的注解
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
createPlot.ax1.annotate(nodeTxt,xy=parentPt,
xycoords='axes fraction',
xytext=centerPt,textcoords='axes fraction',
va='center',ha='center',bbox=nodeType,
arrowprops=arrows_args)
# 在父子节点间填充文本信息
def plotMidText(cntrPt,parentPt,txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
print('%.2f'%xMid,',','%.2f' % yMid)
createPlot.ax1.text(xMid,yMid,txtString, va="center", ha="center", rotation=30)
def plotTree(myTree,parentPt,nodeTxt):
# 求出宽和高
LeafsCnt=0
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstStides = list(myTree.keys())
firstStr = firstStides[0]
# 按照叶子结点个数划分x轴 cntrPt 即当前节点坐标
cntrPt = (plotTree.xOff + (0.1 + float(numLeafs)) /2.0/plotTree.totalW,plotTree.yOff)
plotMidText(cntrPt,parentPt,nodeTxt)
plotNode(firstStr,cntrPt,parentPt,decisionNode)
secondDict = myTree[firstStr]
# y方向上的摆放位置 自上而下绘制,因此递减y值
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key],cntrPt,str(key)) #深度递增 采用py.func.var 作为全局变量使用
else:
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW # x方向计算结点坐标
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) # 绘制
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) # 添加文本信息
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD # 当前层遍历结束
# 主函数
def createPlot(inTree):
# 创建一个新图形并清空绘图区
fig = plt.figure(1,facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
LeafsCnt=0
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '') #x=0.5 ,y=1 中间居上位置
plt.show()
#做个简单的例子,理解DT Tree与binary tree的创建实际相同
#中序遍历与前序的结果创建二叉树
def CreateBinaryTree(InLst,PreLst):
#前序遍历的第一个节点是中间节点A
#终止条件
assert(len(InLst)== len(PreLst))
if len(InLst)< 1: return 'leaf'
A= PreLst[0]
leftPart= InLst.index(A)
myTree= {A:{}}
myTree[A]['left'] = CreateBinaryTree(InLst[:leftPart], PreLst[1:leftPart+1] )
myTree[A]['right'] = CreateBinaryTree(InLst[leftPart+1:],PreLst[leftPart+1:])
return myTree
def test1():
lenses = pd.read_csv('lenses.txt',header= None, names=['age','prescript','astigmatic','tearRate','label'] ,sep = '\t')
myData = createTree(lenses)
#storeTree(myData,'decisionTree1.pickle')
#myData= grabTree('decisionTree1.pickle')
#getTreeDepth(myData)
createPlot(myData)
##做个简单的例子,理解DT Tree与binary tree的创建是一个过程
def test2():
InLst= [4,2,1,5,3,6]
PreLst= [1,2,4,3,5,6]
myData = CreateBinaryTree(InLst,PreLst)
#getNumLeafs(myData)
#getTreeDepth(myData)
createPlot(myData)
if __name__ == '__main__':
test1()
- 画出的决策树结构,注意这里已经修正原作者wj-1314代码中的一个Bug ,所以看起来更加美观