LeetCode 494目标和 背包模型给出动态规划的解法

0. 假设有一种 满足和为S的+- 组合序列 ，正数的和为X ,则 | 负数 | （绝对值）之和为 oldSum-X
   0-（oldSum-X) + X = S ,则X= （oldSum+S)/2 , 问题转化为正数序列中和为X的子集的个数

1. 背包问题

   DP含义

   设dp[i][j]表示背包大小为j时候 前i个元素多少组组合满足恰好“装满”的情况

   通过是否往背包装或不装Sizes[i] 来确定转移方程

   • 不装Sizes[i]: dp[i-1][j]
   • 装Sizes[i]: j>=Size[i] and dp[i-1][j-Sizes[i]]
   • 即 dp[i][j]= dp[i-1][j]+ dp[i-1][j-Sizes[i]] with j>=Size[i]

   举例验证

   

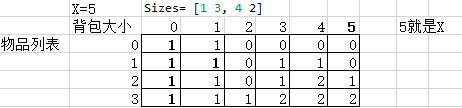
2. 背包问题适用于问题是正数的情况 即物品应该有大小属性 ，否则背包模型不成立

   • 抽出有大小的物品 filterNums 组合个数记Y
   • 剩下的全0 数组(长度是n)的组合个数有2^n

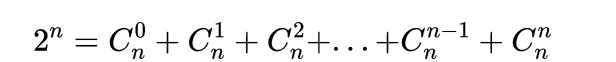
- 最终结果 = Y *2^n

3. ((oldSum+S) %2 || S > oldSum|| ) 的写法会导致 signed integer overflow 如S=2^32-1
   应该写成 (S > oldSum|| (oldSum+S) %2)

class Solution {
public:
//问题1  背包问题
//问题2 0 问题
//问题3 integer overflow
    int findTargetSumWays(vector<int>& nums, int S) {
      //采用暴力搜索 For循环 or 回溯   会超时
      //正数之和X= (oldSum+S)/2  , (oldSum+S) is even and X<=oldSum

      int oldSum=0;
      std::vector<int> filterNums;
      filterNums.reserve(nums.size());
      for (const int & t:nums)
      {
        if(t!=0)
        {
            filterNums.emplace_back(t);
            oldSum+=t;
        }
        
      } 

      if(filterNums.size()== 0 ) return (int)std::pow(2,nums.size()- filterNums.size()) ; //元素全是0    2^n= Cn0+ Cn1...+ Cnn 
      if( (S > oldSum|| (oldSum+S) %2)  )   return 0;   //oldSum+S may  signed integer overflow  判断逻辑S < oldSum 在前
      
    
      int X= (oldSum +S)/2;

      //问题转化为填满大小为X的背包 从Sizes中取元素有几种方法  位置不同 也是一种新的方法 如 [1 1 2  1]  ( 1 _ 2) and  (_ 1 2) this different
      //dp[i][j]= dp[i-1][j]+ dp[i-1][j-Sizes[i]] with j>=Size[i]
       std::vector<std::vector<int>> dp(filterNums.size(), std::vector<int>(X+1,0) );
       //put 0 thing
       for(int jBag=0;jBag<=X;jBag++)
       {
           if(jBag==0 || jBag == filterNums[0] ) dp[0][jBag]=1;
       }
       //put 1.. thing
       for(int iThing =1 ;iThing<filterNums.size();iThing++)
       {
     
              for(int jBag=0;jBag<=X;jBag++)
              {
                  dp[iThing][jBag] = dp[iThing-1][jBag] ;
                  //[0,0,1] 测试用例时候出错 说明背包问题有限定条件 要是物品必须要有大小
                  if(jBag>=filterNums[iThing])   dp[iThing][jBag]+= dp[iThing-1][jBag-filterNums[iThing]];
              }
          
   
       }
       
       	for (const auto & x : dp)
        {
            for (const auto & t : x) std::cout << t << " ";
            std::cout << std::endl;
        }
    
    return dp[filterNums.size()-1][X] *(int)std::pow(2,nums.size()- filterNums.size()) ;

    }
};