并查集小专题
并查集,不复杂,但是我一直不甚理解,用得不好。这几天对并查集做了些针对性训练。算了有了一个初步的了解。这里稍微进行一下整理。
poj 1308
给定一个图的一些边 判断这个图是不是树。
利用并查集,把联结的点放在同一集合,利用findset判断是否存在环。
需要注意的是,森林不是树,所以讲边扫描完毕后,需要遍历每个点,看看有几个点是入度为零的,如果只有一个点是入度为零,那么就是树;不然就是森林了。
1: /* 1: 0 0 空树是一棵树
2: 2: 1 1 0 0 不是树 不能自己指向自己
3: 3: 1 2 1 2 0 0 不是树....自己开始一直在这么WA 好郁闷 重复都不行呀~~5555
4: 4: 1 2 2 3 4 5 不是树 森林不算是树(主要是注意自己)
5: 5: 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 1 注意 一个节点在指向自己的父亲或祖先 都是错误的 即 9-->1 错
6: 6: 1 2 2 1 0 0 也是错误的
7: */
8: #include <iostream>
9: #include <cstdio>
10: #include <cstring>
11: using namespace std;
12: const int maxn = 1010;
13: int father[maxn];
14: bool visit[maxn],od[maxn];
15: int getfather(int u)
16: {17: if(father[u] == u) return u;
18: else return getfather(father[u]);
19: }20: bool findset(int u, int v)
21: {22: if(getfather(u) == getfather(v))
23: return true;
24: else return false;
25: }26: void united(int u, int v)
27: {28: int uu = getfather(u);
29: int vv = getfather(v);
30: father[vv] = uu; 31: }32: int main()
33: {34: //freopen("test.txt","r",stdin);
35: int x,y,cas=0;
36: bool flag;
37: while(++cas)
38: { 39: flag = true;40: for(int i=1;i<=maxn-10;++i)
41: father[i] = i;42: memset(visit,false,sizeof(visit));
43: memset(od,false,sizeof(od));
44: while(scanf("%d%d",&x,&y) && x>0 && y>0)
45: {46: if(x==y)
47: { 48: flag = false;49: while(scanf("%d%d",&x,&y) && x!=0);
50: break;
51: }52: if(findset(x,y))
53: { 54: flag = false;55: while(scanf("%d%d",&x,&y) && x!=0);
56: break;
57: }58: else
59: { 60: united(x,y); 61: visit[y] = true; 62: visit[x] = true; 63: od[y] = true; 64: } 65: }66: if(x==-1) break;
67: int cnt = 0;
68: for(int i=1;i<=maxn-10;++i)
69: {70: if(visit[i] == true && od[i] == false)
71: ++cnt;72: if(cnt>1)
73: { 74: flag = false;75: break;
76: } 77: }78: if(flag) printf("Case %d is a tree.\n",cas);
79: else printf("Case %d is not a tree.\n",cas);
80: } 81: }
poj 1611
最基本的并查集应用,给定一些集合和一个特定元素,输出与这个特定元素属于同一集合的所有元素数。直接计数即可。代码略。
poj 1703
相当于简化的食物链问题,从原来的三个种类变成两个种类。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: using namespace std;
5: int father[100010],dis[100010];
6: int getfather(int u)
7: {8: int s;
9: if(father[u] == u)
10: return u;
11: else s = getfather(father[u]);
12: dis[u] = (dis[father[u]]+dis[u])%2; 13: father[u] = s;14: return s;
15: }16: int main()
17: {18: freopen("test.txt","r",stdin);
19: int cas,n,m,a,b;
20: scanf("%d",&cas);
21: while(cas--)
22: {23: scanf("%d%d",&n,&m);
24: for(int i=1;i<=n;++i)
25: father[i] = i;26: memset(dis,0,sizeof(dis));
27: char op[10];
28: for(int i=0;i<m;++i)
29: {30: scanf("%s%d%d",op,&a,&b);
31: int fa = getfather(a);
32: int fb = getfather(b);
33: if(op[0] == 'D')
34: {35: if(fa!=fb)
36: { 37: father[fa]= fb; 38: dis[fa] = (dis[b]-dis[a]+1)%2; 39: } 40: }41: else
42: {43: if(fa != fb)
44: printf("Not sure yet.\n");
45: else if((dis[a]-dis[b]+2)%2==0)
46: printf("In the same gang.\n");
47: else printf("In different gangs.\n");
48: } 49: } 50: }51: return 0;
52: }Cube Stacking
Time Limit: 2000MS
Memory Limit: 30000K
Total Submissions: 13782
Accepted: 4648
Case Time Limit: 1000MS
Description
Farmer John and Betsy are playing a game with N (1 <= N <= 30,000)identical cubes labeled 1 through N. They start with N stacks, each containing a single cube. Farmer John asks Betsy to perform P (1<= P <= 100,000) operation. There are two types of operations:
moves and counts.
* In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
* In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.
Write a program that can verify the results of the game.
Input
* Line 1: A single integer, P
* Lines 2..P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a 'M' for a move operation or a 'C' for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.
Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.
Output
Print the output from each of the count operations in the same order as the input file.
Sample Input
6 M 1 6 C 1 M 2 4 M 2 6 C 3 C 4
Sample Output
1 0 2
Source
题意大致是把cube堆成stack,问任一时候某一cube下面有多少cube。思路是将每个stack看成一个集合,最下面的cube为根结点。建立dis数组,用来记录每个cube下面还有多少其他cube,建立cnt数组,记录每个stack由多少cube组成。需要注意的是两个stack合并时,cnt和dis的处理。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: using namespace std;
5: int father[30010],cnt[30010],dis[30010],n;
6: int getfather(int u)
7: {8: int s;
9: if(father[u] == u)
10: {11: return u;
12: }13: else s = getfather(father[u]);
14: dis[u]+=dis[father[u]]; 15: father[u] =s;16: return s;
17: }18: void unionset(int u, int v)
19: {20: int fu = getfather(u);
21: int fv = getfather(v);
22: if(fu!=fv)
23: { 24: father[fu] = fv;25: //dis[u] += cnt[fv];
26: dis[fu]+=cnt[fv]; 27: cnt[fv]+= cnt[fu]; 28: } 29: }30: int main()
31: {32: //freopen("test.txt","r",stdin);
33: scanf("%d",&n);
34: char op[3];
35: int a,b,len;
36: for(int i=1;i<=30000;++i)
37: { 38: father[i] = i; 39: cnt[i] = 1; 40: dis[i] = 0; 41: }42: while(scanf("%s",op)!=EOF)
43: {44: if(op[0] == 'M')
45: {46: scanf("%d%d",&a,&b);
47: unionset(a,b); 48: }49: else
50: {51: scanf("%d",&a);
52: int fa = getfather(a);
53: printf("%d\n",dis[a]);
54: } 55: }56: return 0;
57: }
poj 2236
Wireless Network
Time Limit: 10000MS
Memory Limit: 65536K
Total Submissions: 11563
Accepted: 4914
Description
An earthquake takes place in Southeast Asia. The ACM (Asia Cooperated Medical team) have set up a wireless network with the lap computers, but an unexpected aftershock attacked, all computers in the network were all broken. The computers are repaired one by one, and the network gradually began to work again. Because of the hardware restricts, each computer can only directly communicate with the computers that are not farther than d meters from it. But every computer can be regarded as the intermediary of the communication between two other computers, that is to say computer A and computer B can communicate if computer A and computer B can communicate directly or there is a computer C that can communicate with both A and B.
In the process of repairing the network, workers can take two kinds of operations at every moment, repairing a computer, or testing if two computers can communicate. Your job is to answer all the testing operations.
Input
The first line contains two integers N and d (1 <= N <= 1001, 0 <= d <= 20000). Here N is the number of computers, which are numbered from 1 to N, and D is the maximum distance two computers can communicate directly. In the next N lines, each contains two integers xi, yi (0 <= xi, yi <= 10000), which is the coordinate of N computers. From the (N+1)-th line to the end of input, there are operations, which are carried out one by one. Each line contains an operation in one of following two formats:
1. "O p" (1 <= p <= N), which means repairing computer p.
2. "S p q" (1 <= p, q <= N), which means testing whether computer p and q can communicate.
The input will not exceed 300000 lines.
Output
For each Testing operation, print "SUCCESS" if the two computers can communicate, or "FAIL" if not.
Sample Input
4 1 0 1 0 2 0 3 0 4 O 1 O 2 O 4 S 1 4 O 3 S 1 4
Sample Output
FAIL SUCCESS
Source
POJ Monthly,HQM
题目大意是:一定距离范围内的computer可以通信,不过加入了一个时间维度,所以需要读一个扫一次建立并查集。
1: #include <iostream>
2: #include <cmath>
3: #include <cstdio>
4: #include <cstring>
5: using namespace std;
6: struct node{
7: int x;
8: int y;
9: }p[1020];10: int father[1020],n,d;
11: bool check[1020];
12: double dis(const node &a, const node &b)
13: {14: return sqrt((double)(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
15: }16: double getfather(int u)
17: {18: if(father[u] == u)
19: return u;
20: else return getfather(father[u]);
21: }22: void unionset(int u, int v)
23: {24: int fu = getfather(u);
25: int fv = getfather(v);
26: if(fu!=fv)
27: father[fu] = fv; 28: }29: bool findset(int u, int v)
30: {31: int fu = getfather(u);
32: int fv = getfather(v);
33: if(fu == fv)
34: return true;
35: else return false;
36: }37: int main()
38: {39: freopen("test.txt","r",stdin);
40: scanf("%d%d",&n,&d);
41: for(int i=1;i<=n;++i)
42: { 43: father[i] = i; 44: check[i] = false; 45: }46: for(int i=1;i<=n;++i)
47: scanf("%d%d",&p[i].x, &p[i].y);
48: char op[3];
49: int a,b;
50: while(scanf("%s",op) != EOF)
51: {52: if(op[0] == 'O')
53: {54: scanf("%d",&a);
55: check[a] = true;56: for(int i=1;i<=n;++i)
57: {58: if(dis(p[a],p[i])<=d && check[i])
59: unionset(a,i); 60: } 61: }62: else if(op[0] == 'S')
63: {64: scanf("%d%d",&a,&b);
65: if(findset(a,b))
66: printf("SUCCESS\n");
67: else printf("FAIL\n");
68: } 69: }70: return 0;
71: }
poj 2492
这个问题跟1703完全类似,就是简化版的食物链。代码略。
poj 1456
Supermarket
Time Limit: 2000MS
Memory Limit: 65536K
Total Submissions: 6472
Accepted: 2673
Description
A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σx∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.
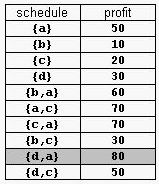
Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.
Input
A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.
Output
For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.
Sample Input
4 50 2 10 1 20 2 30 1 7 20 1 2 1 10 3 100 2 8 2 5 20 50 10
Sample Output
80 185
Hint
The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.
Source
题目大意是:每个物品都有profit和销售日期的deadline。每天只能销售一件物品,如何安排销售日期能够获得最大利润?
显然应该从profit最大的物品开始安排,而且就安排在deadline,因为如果不这样,总的利润不最大。(为什么?)一旦一个deadline被安排销售了某个物品,那么这个deadline与之前一个unionset。然后继续从profit次大的物品开始。
1: #include <iostream>
2: #include <cstdio>
3: #include <algorithm>
4: #include <cstring>
5: using namespace std;
6: struct node{
7: int pr;
8: int due;
9: }p[10010];10: int father[10010];
11: bool check[10010];
12: int n;
13: long long sum;
14: bool cmp(const node &a, const node &b)
15: {16: if(a.pr>b.pr)
17: return 1;
18: else return 0;
19: }20: int getfather(int u)
21: {22: if(father[u] == u)
23: return u;
24: else return getfather(father[u]);
25: }26: void united(int u, int v)
27: {28: int uu = getfather(u);
29: int vv = getfather(v);
30: father[uu] = vv; 31: }32: int main()
33: {34: //freopen("test.txt","r",stdin);
35: while(scanf("%d",&n)!= EOF)
36: {37: for(int i=0;i<n;++i)
38: scanf("%d%d",&p[i].pr,&p[i].due);
39: for(int i=1;i<=10000;++i)
40: father[i] = i;41: memset(check,false,sizeof(check));
42: sort(p,p+n,cmp); 43: sum = 0;44: for(int i=0;i<n;++i)
45: {46: int temp = getfather(p[i].due);
47: if(check[temp] == false)
48: { 49: sum+=p[i].pr; 50: check[temp] = true;51: if(temp!=1)
52: united(temp,temp-1); 53: } 54: }55: printf("%d\n",sum);
56: } 57: }
poj 1733 parity game
Parity game
Time Limit: 1000MS
Memory Limit: 65536K
Total Submissions: 4229
Accepted: 1658
Description
Now and then you play the following game with your friend. Your friend writes down a sequence consisting of zeroes and ones. You choose a continuous subsequence (for example the subsequence from the third to the fifth digit inclusively) and ask him, whether this subsequence contains even or odd number of ones. Your friend answers your question and you can ask him about another subsequence and so on. Your task is to guess the entire sequence of numbers.
You suspect some of your friend's answers may not be correct and you want to convict him of falsehood. Thus you have decided to write a program to help you in this matter. The program will receive a series of your questions together with the answers you have received from your friend. The aim of this program is to find the first answer which is provably wrong, i.e. that there exists a sequence satisfying answers to all the previous questions, but no such sequence satisfies this answer.
Input
The first line of input contains one number, which is the length of the sequence of zeroes and ones. This length is less or equal to 1000000000. In the second line, there is one positive integer which is the number of questions asked and answers to them. The number of questions and answers is less or equal to 5000. The remaining lines specify questions and answers. Each line contains one question and the answer to this question: two integers (the position of the first and last digit in the chosen subsequence) and one word which is either `even' or `odd' (the answer, i.e. the parity of the number of ones in the chosen subsequence, where `even' means an even number of ones and `odd' means an odd number).
Output
There is only one line in output containing one integer X. Number X says that there exists a sequence of zeroes and ones satisfying first X parity conditions, but there exists none satisfying X+1 conditions. If there exists a sequence of zeroes and ones satisfying all the given conditions, then number X should be the number of all the questions asked.
Sample Input
10 5 1 2 even 3 4 odd 5 6 even 1 6 even 7 10 odd
Sample Output
3
Source
首先需要利用map进行离散化。因为原题中10^9这个区间太大了,而真正用到了最多10000个不同的端点。另外的一个技巧是,为了让区间连续便于识别,记录是从闭区间[a,b]改成半开半闭区间[a,b+1)。每次读进来a,b,先将b自加,然后判断,他们如果属于同一个集合,就可以判断是不是合法。否则就可以把根结点较小的集合合并到根结点较大的集合。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: #include <map>
5: using namespace std;
6: const int maxn = 10005;
7: map<int,int> mapping;
8: int father[maxn],dis[maxn];
9: int getfather(int u)
10: {11: int s;
12: if(father[u] == u)
13: return u;
14: else s = getfather(father[u]);
15: dis[u] = dis[u]^dis[father[u]]; 16: father[u] = s;17: return s;
18: }19: int main()
20: {21: freopen("test.txt","r",stdin);
22: int n,m,index=1,a,b,x,y,temp;
23: char str[10];
24: scanf("%d%d",&n,&m);
25: for(int i=1;i<maxn;++i)
26: { 27: father[i] = i; 28: dis[i] = 0; 29: }30: int j;
31: for(j = 1;j<=m;++j)
32: {33: scanf("%d%d%s",&a,&b,str);
34: b++;35: if(mapping.find(a) == mapping.end())
36: { 37: mapping[a] = index; 38: ++index; 39: }40: if(mapping.find(b) == mapping.end())
41: { 42: mapping[b] = index; 43: ++index; 44: } 45: x = mapping[a]; 46: y = mapping[b];47: if(str[0] == 'o')
48: temp = 1;49: else temp = 0;
50: int fx = getfather(x);
51: int fy = getfather(y);
52: if(fx == fy)
53: {54: if(temp!=dis[x]^dis[y])
55: break;
56: }57: else
58: {59: if(fx < fy)
60: { 61: dis[fx] = temp^dis[x]^dis[y]; 62: father[fx] = fy; 63: }64: else
65: { 66: dis[fy] = temp^dis[x]^dis[y]; 67: father[fy] = fx; 68: } 69: } 70: }71: printf("%d\n",j-1);
72: return 0;
73: }
hdu 3038
这个题目与poj 1733基本类似,这道题不需要离散化,只需要将公式重新推导一下即可。代码略。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: using namespace std;
5: int father[200010],dis[200010];
6: int getfather(int u)
7: {8: int s;
9: if(father[u] == u)
10: return u;
11: else s = getfather(father[u]);
12: dis[u] = dis[u]+dis[father[u]]; 13: father[u] = s;14: return s;
15: }16: int main()
17: {18: //freopen("test.txt","r",stdin);
19: int n,m,a,b,c,cnt = 0;
20: while(scanf("%d%d",&n,&m)!=EOF)
21: { 22: cnt = 0;23: for(int i=1;i<=n+1;++i)
24: { 25: father[i] = i; 26: dis[i] = 0; 27: }28: for(int i=0;i<m;++i)
29: {30: scanf("%d%d%d",&a,&b,&c);
31: b++;32: int fa = getfather(a);
33: int fb = getfather(b);
34: if(fa == fb && dis[a]-dis[b]!=c)
35: ++cnt;36: else if(fa!=fb)
37: {38: if(fa<fb)
39: { 40: dis[fa] = c-dis[a]+dis[b]; 41: father[fa] = fb; 42: }43: else
44: { 45: dis[fb] = dis[a]-c-dis[b]; 46: father[fb] = fa; 47: } 48: } 49: }50: printf("%d\n",cnt);
51: }52: return 0;
53: }
poj 1417 True liars
True Liars
Time Limit: 1000MS
Memory Limit: 10000K
Total Submissions: 1340
Accepted: 382
Description
After having drifted about in a small boat for a couple of days, Akira Crusoe Maeda was finally cast ashore on a foggy island. Though he was exhausted and despaired, he was still fortunate to remember a legend of the foggy island, which he had heard from patriarchs in his childhood. This must be the island in the legend. In the legend, two tribes have inhabited the island, one is divine and the other is devilish, once members of the divine tribe bless you, your future is bright and promising, and your soul will eventually go to Heaven, in contrast, once members of the devilish tribe curse you, your future is bleak and hopeless, and your soul will eventually fall down to Hell.
In order to prevent the worst-case scenario, Akira should distinguish the devilish from the divine. But how? They looked exactly alike and he could not distinguish one from the other solely by their appearances. He still had his last hope, however. The members of the divine tribe are truth-tellers, that is, they always tell the truth and those of the devilish tribe are liars, that is, they always tell a lie.
He asked some of them whether or not some are divine. They knew one another very much and always responded to him "faithfully" according to their individual natures (i.e., they always tell the truth or always a lie). He did not dare to ask any other forms of questions, since the legend says that a devilish member would curse a person forever when he did not like the question. He had another piece of useful informationf the legend tells the populations of both tribes. These numbers in the legend are trustworthy since everyone living on this island is immortal and none have ever been born at least these millennia.
You are a good computer programmer and so requested to help Akira by writing a program that classifies the inhabitants according to their answers to his inquiries.
Input
The input consists of multiple data sets, each in the following format :
n p1 p2
xl yl a1
x2 y2 a2
...
xi yi ai
...
xn yn an
The first line has three non-negative integers n, p1, and p2. n is the number of questions Akira asked. pl and p2 are the populations of the divine and devilish tribes, respectively, in the legend. Each of the following n lines has two integers xi, yi and one word ai. xi and yi are the identification numbers of inhabitants, each of which is between 1 and p1 + p2, inclusive. ai is either yes, if the inhabitant xi said that the inhabitant yi was a member of the divine tribe, or no, otherwise. Note that xi and yi can be the same number since "are you a member of the divine tribe?" is a valid question. Note also that two lines may have the same x's and y's since Akira was very upset and might have asked the same question to the same one more than once.
You may assume that n is less than 1000 and that p1 and p2 are less than 300. A line with three zeros, i.e., 0 0 0, represents the end of the input. You can assume that each data set is consistent and no contradictory answers are included.
Output
For each data set, if it includes sufficient information to classify all the inhabitants, print the identification numbers of all the divine ones in ascending order, one in a line. In addition, following the output numbers, print end in a line. Otherwise, i.e., if a given data set does not include sufficient information to identify all the divine members, print no in a line.
Sample Input
2 1 1 1 2 no 2 1 no 3 2 1 1 1 yes 2 2 yes 3 3 yes 2 2 1 1 2 yes 2 3 no 5 4 3 1 2 yes 1 3 no 4 5 yes 5 6 yes 6 7 no 0 0 0
Sample Output
no no 1 2 end 3 4 5 6 end
Source
这个题目比较有意思。首先划分清楚说话的含义。a b no <=> a和b属于不同tribe。a b yes <=> a和b属于同一tribe。知道了这一点,就可以利用poj1703,2492的思想进行并查集划分,经过这一步,所有的人被分成了不同的组。每个组的人根据dis不同可以分为两个部分,人数分别为m1和m2个。问题是现在不清楚m1,m2哪个对应divine,哪个对应devil。题目的问题是所给信息是否足够找出所有divine。通过参考网上资料,这个问题可以通过dp得到完满解决。用dp[i][j]表示扫描到第i组人时一共有j个divine的总的情况数。递归方程为:
dp[i][j] = dp[i][j - m_1 ] + dp[i][j - m_2 ](j - m_1 \ge 0,\;\;j - m_2 \ge 0)
如果最后dp[总组数][总divine数] == 1则可以确定哪些是divine,否则就不行。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: #include <algorithm>
5: //#include <utility>
6: #include <vector>
7: using namespace std;
8: int father[610],dis[610],group[610];
9: int dp[610][610];
10: bool visit[610];
11: int n,divine,devil,m;
12: bool flag;
13: vector<int> v;
14: 15: int getfather(int u)
16: {17: int s;
18: if(father[u] == u)
19: return u;
20: else s = getfather(father[u]);
21: dis[u] = dis[u]^dis[father[u]]; 22: father[u] = s;23: return s;
24: }25: void push(int u, int g)
26: {27: for(int i=1;i<=n;++i)
28: {29: if(dis[i] == u && group[i] == g)
30: v.push_back(i); 31: } 32: }33: int main()
34: {35: freopen("test.txt","r",stdin);
36: while(scanf("%d%d%d",&m,&divine,&devil) && (m||divine||devil))
37: {38: if(m == 0)
39: {40: if(divine == 0 )
41: printf("end\n");
42: else if(divine !=0 && devil == 0)
43: {44: for(int i=1;i<=divine;++i)
45: printf("%d\n",i);
46: printf("end\n");
47: }48: else
49: printf("no\n");
50: continue;
51: } 52: flag = true; 53: n = divine+devil; 54: for(int i=1;i<=n;++i) //0---same 1---opposite
55: { 56: father[i] = i; 57: dis[i] = 0; 58: }59: int a,b,c;
60: char str[5];
61: for(int i=0;i<m;++i)
62: {63: scanf("%d%d%s",&a,&b,str);
64: if(str[0] == 'y')
65: c = 0;66: else c = 1;
67: int fa = getfather(a);
68: int fb = getfather(b);
69: if(fa == fb && (dis[a]^dis[b])!=c)
70: { 71: flag = false; 72: }73: else if(fa!=fb)
74: { 75: dis[fa] = c^dis[b]^dis[a]; 76: father[fa] = fb; 77: } 78: }79: memset(visit,false,sizeof(visit));
80: int f,setnum=0,recount[610][2];
81: memset(recount,0,sizeof(recount));
82: for(int i=1;i<=n;++i)
83: {84: if(!visit[i])
85: { 86: f = getfather(i); 87: setnum++;88: if(dis[i] == 0)
89: recount[setnum][0]++;90: else recount[setnum][1]++;
91: visit[i] = true; 92: group[i] = setnum;93: for(int j=i+1;j<=n;++j)
94: {95: if(!visit[j] && getfather(j) == f)
96: { 97: visit[j] = true; 98: group[j] = setnum;99: if(dis[j] == 0)
100: recount[setnum][0]++;101: else recount[setnum][1]++;
102: } 103: } 104: } 105: }106: memset(dp,0,sizeof(dp));
107: v.clear();108: int buffer;
109: int s = divine;
110: dp[1][recount[1][0]] += 1; 111: dp[1][recount[1][1]] += 1;112: for(int i=2;i<=setnum;++i)
113: for(int j=0;j<=divine;++j)
114: { 115: buffer = 0;116: if(j-recount[i][0]>=0)
117: buffer = dp[i-1][j-recount[i][0]];118: if(j-recount[i][1]>=0)
119: buffer += dp[i-1][j-recount[i][1]];120: if(buffer>=2)
121: buffer = 2; 122: dp[i][j] = buffer; 123: }124: if(dp[setnum][divine] == 1)
125: {126: for(int i=setnum-1;i>=1;--i)
127: {128: if(dp[i][s-recount[i+1][0]] == 1)
129: { 130: push(0,i+1); 131: s -=recount[i+1][0]; 132: }133: else
134: { 135: push(1,i+1); 136: s -=recount[i+1][1]; 137: } 138: }139: if(s == recount[1][0])
140: push(0,1);141: else push(1,1);
142: sort(v.begin(),v.end());143: vector <int> ::iterator iter = v.begin();
144: for ( ; iter != v.end(); ++iter)
145: { 146: printf("%d\n",*iter);
147: } 148: printf("end\n");
149: }150: else printf("no\n");
151: } 152: }poj 2912
Rochambeau
Time Limit: 5000MS
Memory Limit: 65536K
Total Submissions: 1248
Accepted: 422
Description
N children are playing Rochambeau (scissors-rock-cloth) game with you. One of them is the judge. The rest children are divided into three groups (it is possible that some group is empty). You don’t know who is the judge, or how the children are grouped. Then the children start playing Rochambeau game for M rounds. Each round two children are arbitrarily selected to play Rochambeau for one once, and you will be told the outcome while not knowing which gesture the children presented. It is known that the children in the same group would present the same gesture (hence, two children in the same group always get draw when playing) and different groups for different gestures. The judge would present gesture randomly each time, hence no one knows what gesture the judge would present. Can you guess who is the judge after after the game ends? If you can, after how many rounds can you find out the judge at the earliest?
Input
Input contains multiple test cases. Each test case starts with two integers N and M (1 ≤ N ≤ 500, 0 ≤ M ≤ 2,000) in one line, which are the number of children and the number of rounds. Following are M lines, each line contains two integers in [0, N) separated by one symbol. The two integers are the IDs of the two children selected to play Rochambeau for this round. The symbol may be “=”, “>” or “<”, referring to a draw, that first child wins and that second child wins respectively.
Output
There is only one line for each test case. If the judge can be found, print the ID of the judge, and the least number of rounds after which the judge can be uniquely determined. If the judge can not be found, or the outcomes of the M rounds of game are inconsistent, print the corresponding message.
Sample Input
3 3 0<1 1<2 2<0 3 5 0<1 0>1 1<2 1>2 0<2 4 4 0<1 0>1 2<3 2>3 1 0
Sample Output
Can not determine Player 1 can be determined to be the judge after 4 lines Impossible Player 0 can be determined to be the judge after 0 lines
Source
Baidu Star 2006 Preliminary
Chen, Shixi (xreborner) living in http://fairyair.yeah.net/
这都题很食物链很相似,但是多出来一个judge的角色。判断谁是judge时可以采用枚举的办法:
1. 如果只有1个小孩是judge时全部语句都是正确的,说明该小孩是judge,那么判断的句子数即为其他小孩的err[i]的最大值。如果
2. 如果每个小孩的都不是judge(即都可以找到出错的语句),那么就是impossible。
3. 多于1个小孩是judge时没有找到出错的语句,就是Can not determine。
1: #include <iostream>
2: #include <cstdio>
3: #include <cstring>
4: using namespace std;
5: int father[550],dis[550],err[550];
6: int a[2010],c[2010];
7: char b[2010];
8: int n,m;
9: int getfather(int u)
10: {11: int s;
12: if(father[u] == u)
13: return u;
14: else s = getfather(father[u]);
15: dis[u] = (dis[u]+dis[father[u]])%3; 16: father[u] = s;17: return s;
18: } 19: 20: int main()
21: {22: freopen("test.txt","r",stdin);
23: int judge,temp;
24: while(scanf("%d%d",&n,&m) != EOF)
25: {26: for(int i=0;i<m;++i)
27: scanf("%d%c%d",a+i,&b[i],c+i);
28: memset(err,-1,sizeof(err));
29: for(judge = 0;judge<n;++judge)
30: {31: for(int i=0;i<n;++i)
32: { 33: father[i] = i; 34: dis[i] = 0; 35: }36: for(int i=0;i<m;++i)
37: {38: if(a[i] == judge || c[i] == judge)
39: continue;
40: if(b[i] == '=') temp = 0;
41: else if(b[i] == '<') temp = 1;
42: else temp = 2;
43: int fa = getfather(a[i]);
44: int fc = getfather(c[i]);
45: if(fa == fc)
46: { 47: if((dis[a[i]]-dis[c[i]]+3)%3!=temp)
48: { 49: err[judge] = i+1;50: break;
51: } 52: }53: else
54: { 55: dis[fa] = (temp+dis[c[i]]-dis[a[i]]+3)%3; 56: father[fa] = fc; 57: } 58: } 59: }60: int player=0,num=0,pos=0;
61: for(int i=0;i<n;++i)
62: {63: if(err[i]==-1)
64: { 65: ++num; 66: player = i; 67: } 68: pos = max(pos,err[i]); 69: }70: if(num == 0)
71: printf("Impossible\n");
72: else if(num == 1)
73: printf("Player %d can be determined to be the judge after %d lines\n",player,pos);
74: else printf("Can not determine\n");
75: 76: } 77: }


