poj 1182 并查集

并查集是十分有用的数据结果，对于一般人来说，这个应当是十分简单的应用，但是对于我来说却不然。上次比赛的时候有个题目就是因为自己并查集写得有问题而WA了好几次。。。

1182这道题目的大意是：有ABC三个物种，A吃B，B吃C，C吃A。现在有N个编号的个体（1-N），不知道每个个体分别属于哪个物种。现在有K条语句，每条语句有两种形式：

1. 1 a b 表示编号为a和b的个体属于同一个物种；
2. 2 a b表示编号为a的个体吃b；

这些判断语句不一定全为真。一条判断语句为假的条件是：

1. a，b大于N；
2. 2 a a；
3. 与前矛盾；

现在的问题是判断到底有多少条语句是假。

网上看到的解决方法。经典的并查集应用。这个问题的关键，我觉得是应该注意到进食的回环关系，并且在数学上对这个关系进行表示，那就是模运算。建立辅助数组dis[N]，表示每个结点到其根节点的距离。dis[i]=0表示该结点和根节点属于同一物种。dis[i]=1该结点物种吃根节点。dis[i]=2表示根结点物种吃该结点。这样每条语句相当于就是在对并查集进行操作了。这里需要注意的是判断和路径压缩。

先说判断。任意两个已经建立关系的物种应该根结点相同，这样就很容易算出他们的相对距离，从而检查有无矛盾。

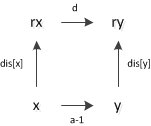
再说路径压缩。也就是新建立关系时应该怎样调整。譬如现在有语句a,x,y。这个a为1或者2。如果此时x,y的根结点不相同，那么他们x到y的距离就应该是a-1。所以x对应的根结点rx到y对应的根结点ry的距离d应该满足：dis[x]+d ==dis[y]+a-1(mod 3)。所以d = (dis[y]-dis[x]+a+2)%3。注意到原来以rx为根的其他节点的dis值应该也要更新。所以getfather过程中进行路径压缩中通知应该更新dis值。

 

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 50010;
int dis[maxn],father[maxn];
int sum;
int getfather(int u)
{
    int s;
    if(father[u] == u) return u;
    else s = getfather(father[u]);
    dis[u] = (dis[u]+dis[father[u]])%3;
    father[u] = s;
    return s;
}
int main()
{
    //freopen("test.txt","r",stdin);
    int n,k,a,x,y,fx,fy,d;
    scanf("%d%d",&n,&k);
    memset(dis,0,sizeof(dis));
    for(int i=0;i<n;++i)
        father[i] = i;
    sum = 0;
    for(int i=0;i<k;++i)
    {
        scanf("%d%d%d",&a,&x,&y);
        fx = getfather(x);
        fy = getfather(y);
        if(x>n || y>n || (a==2 && x==y))
        {
            sum++;
            continue;
        }
        else if(fx == fy)
        {
            if(a==1 && dis[x] != dis[y])
            {sum++;continue;}
            else if(a==2 && (dis[x]-dis[y]+3)%3!=1)
            {sum++;continue;}
        }
        else if(fx != fy)
        {
            d = (a+2+dis[y]-dis[x])%3;
            dis[fx] = d;
            father[fx] = fy;
        }

    }
    printf("%d\n",sum);
}