Cyclic prefix
接触循环签注这个概念已经有一段时间,但是一直没有去思考过。今天想整理一下。
维基百科里面讲得比较清晰。
In telecommunications, the term cyclic prefix refers to the prefixing of a symbol with a repetition of the end. Although the receiver is typically configured to discard the cyclic prefix samples, the cyclic prefix serves two purposes.
- As a guard interval, it eliminates the intersymbol interference from the previous symbol.
- As a repetition of the end of the symbol, it allows the linear convolution of a frequency-selective multipath channel to be modelled as circular convolution, which in turn may be transformed to the frequency domain using a discrete Fourier transform. This approach allows for simple frequency-domain processing, such as channel estimation and equalization.
In order for the cyclic prefix to be effective (i.e. to serve its aforementioned objectives), the length of the cyclic prefix must be at least equal to the length of the multipath channel. Although the concept of cyclic prefix has been traditionally associated with OFDM systems, the cyclic prefix is now also used in single carrier systems to improve the robustness to multipath.
从卷积的概念容易理解1.当循环前缀的长度超过了信道的冲击响应长度时就可以消除码间干扰。2.简化频域的处理。比如信道估计和均衡。
为什么呢?
从维基百科上面的解释来看
Cyclic Prefixes are used in OFDM in order to combat multipath by making channel estimation easy. As an example, consider an OFDM system which has Nsubcarriers[1]. The message symbol can be written as:
The OFDM symbol is constructed by taking the inverse discrete Fourier transform (IDFT) of the message symbol, followed by a cyclic prefixing. Let the symbol obtained by the IDFT be denoted by
![\mathbf{x_0} = [x[0], x[1], \ldots x[N - 1]]^T](http://upload.wikimedia.org/wikipedia/en/math/9/c/8/9c8112f0bfe22b947fe6905d287dac71.png) .
.
Prefixing it with a cyclic prefix of length L − 1, the OFDM symbol obtained is:
![\mathbf{x} = [x[N - L + 1], \ldots x[N - 2], x[N - 1], x[0], x[1], \ldots x[N - 1]]^T](http://upload.wikimedia.org/wikipedia/en/math/3/0/2/3024f352324fff9e6da0f6915efb7be7.png) .
.
Assume that the channel is represented using
![\mathbf{h} = [h_0, h_1, \ldots h_{L-1}]^T](http://upload.wikimedia.org/wikipedia/en/math/9/6/d/96d495e0c152a841b7763e4616d8f86e.png) .
.
Then, after convolution with the channel, which happens as
which is circular convolution, as x[m − k] becomes ![x[(m - k)\mod N]](http://upload.wikimedia.org/wikipedia/en/math/7/0/d/70da65bce81d4148ac272c346912aa48.png) . So, taking the Discrete Fourier Transform, we get
. So, taking the Discrete Fourier Transform, we get
![Y[k] = H[k]\cdot X[k]](http://upload.wikimedia.org/wikipedia/en/math/e/6/4/e649442a57068c5fb97954e0bb6f0b75.png) .
.
where X[k] is the discrete Fourier transform of 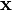 . Thus, a multipath channel is converted into scalar parallel sub-channels in frequency domain, thereby simplifying the receiver design considerably. The task of channel estimation is simplified, as we just need to estimate the scalar coefficients H[k] for each sub-channel and once the values of {H[k]} are estimated, for the duration in which the channel does not vary significantly, merely multiplying the received demodulated symbols by the inverse of H[k] yields the estimates of {X[k]} and hence, the estimate of actual symbols
. Thus, a multipath channel is converted into scalar parallel sub-channels in frequency domain, thereby simplifying the receiver design considerably. The task of channel estimation is simplified, as we just need to estimate the scalar coefficients H[k] for each sub-channel and once the values of {H[k]} are estimated, for the duration in which the channel does not vary significantly, merely multiplying the received demodulated symbols by the inverse of H[k] yields the estimates of {X[k]} and hence, the estimate of actual symbols ![[d_0, d_1, \ldots d_{N - 1}]^T](http://upload.wikimedia.org/wikipedia/en/math/6/8/a/68ac23282a343acb109718a4aeb3acd0.png) .
.
所以说因为有了循环前缀,所以可以使用频域的离散傅里叶变换,这样一来可以大大简化接收器的设计。
用更加数学的语言,矩阵,来看的话,使用了CP以后信道矩阵变成了一个circulant matrix,这种matrix的特点是可以分解成F*D*F^H,其中F是傅立叶矩阵,D是对角矩阵。正是因为D是对角矩阵,就可以理解成每个subcarrier可以看成一个siso系统,可以使用简单的检测方法。具体分析见OFDM_cyclic prefix tutorial。


![\mathbf{d} = [d_0, d_1, \ldots d_{N - 1}]^T](http://upload.wikimedia.org/wikipedia/en/math/b/f/d/bfdad7bd862e83d5ffb13bf94d37b6f7.png)
![y[m] = \sum_{l = 0}^{L - 1} h_l x[m - l] \quad 0 \le m \le N-1](http://upload.wikimedia.org/wikipedia/en/math/c/5/b/c5bdc85026ea0a6e64173e02a9f3ab00.png)
