动态规划 - 最长上升子序列问题

描述

有一个长为n的数列a0，a1，…，an-1。求出这个序列中最长的上升子序列长度。上升子序列指的是对于任意的i < j，都满足ai < aj的子序列。

输入

n = 5

a = {4，2，3，1，5}

输出

3（a1，a2，a4构成的子序列2，3，5最长）

 

这个问题是被称作最长上升子序列的著名问题。这一问题通过DP也能很有效率地求解。我们首先建立递推关系：

定义dp[i]：= 以ai为末尾的最长上升子序列的长度

则，以ai结尾的上升子序列是

只包含ai的子序列，或者

在满足j < i并且aj < ai的以aj结尾的上升子序列末尾，追加上ai后得到的子序列

这样就能得到如下递推关系：

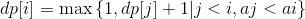
使用这一递推公式可以在O(n²)时间内解决这个问题。

int n;
int a[MAX_N];
int dp[MAX_N];


void solve()
{
    int res = 0;
    for (int i = 0; i < n; i++)
    {
        dp[i] = 1;
        for (int j = 0; j < i; j++)
        {
            if (a[j] < a[i])
            {
                dp[i] = max(dp[i], dp[j]+1);
            }
        }
        res = max(res, dp[i]);
    }
    cout << res << endl;
}