动态规划 - 完全背包问题

有n种重量和价值分别为wi，vi的物品。从这些物品中挑选总重量不超过W的物品，求出挑选物品价值总和的最大值。每种物品可以挑选任意多件。

令dp[i+1][j]:=从前i种物品中挑选总重量不超过j时总价值的最大值。那么递推关系为：

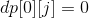
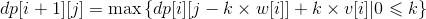
根据递推关系编写代码：

void solve()
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= W; j++)
        {
            for (int k = 0; k * w[i] <= j; k++)
            {
                dp[i+1][j] = max(dp[i+1][j], dp[i][j-k*w[i]] + k * v[i]);
            }
        }
    }
    cout << dp[n][W] << endl;
}

 关于k的循环最坏可能从0循环到W，所以算法复杂度为O(nW²)。

在dp[i+1][j]的计算中选择k(k>=1)个的情况，与在dp[i+1][j-w[i]]的计算中选择k-1个的情况是相同的，所以dp[i+1][j]的递推中k>=1的部分计算已经在dp[i+1][j-w[i]]的计算中完成了。那么可以按照如下方式进行：

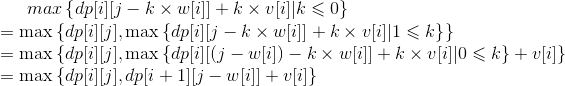
这样一来就不需要关于k的循环了，便可以使用O(nW)时间解决问题。

void solve1()
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= W; j++)
        {
            if (j < w[i])
            {
                dp[i+1][j] = dp[i][j];
            }
            else
            {
                dp[i+1][j] = max(dp[i][j], dp[i+1][j-w[i]]+v[i]);
            }
        }
    }
    cout << dp[n][W] << endl;
}