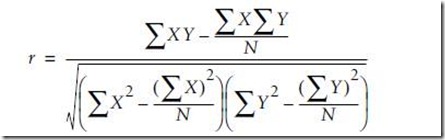C++STL学习之algorithm库函数
本文目的
最近温习了一下C++ STL中的algorithm库函数,记得上次看这些内容时,还在读书,可以追溯到2009年春天了(刚好4年J)。正所谓为“温故而知新,可以为师矣”。闲话少说,开始正文。
算法库
C++标准算法库中包含一些模版函数,用于执行基本的算法,比如for_each(遍历容器),random_shuffle(随机打乱容器)等。主要实现包含在头文件<algorthim>中,少量在<numeric>中。它是STL的三大核心组件之一,其他两个是容器(container,常用数据结构)和迭代器(Iterator,数据结构访问适配器)。设计思想:算法函数通过迭代器作用在容器上,最大程度的复用。比如for_each函数,可以通过迭代器作用在set,map,list,vector,deque等容器上。
所有的算法都会接受容器的迭代器作为参数,而不是容器本身,这样算法可以作用于全部或者部分容器中的元素,十分灵活。如果算法(比如std::transform)需要访问两个容器,一般传入第一个容器的第一个元素,第一个容器的最后一个元素和第二个容器的第一元素。不需要传入第二个容器的最后一个元素,因为可以通过第一个容器的两个迭代器计算出来。除非此算法允许作用在两个不一样长度的容器上,比如search函数。
为了使容器算法函数具有更高的灵活性,一般算法函数会接受一个函数或则函数对象(类似javascript的回调函数),这个函数在算法执行过程中内部使用,执行特殊的业务逻辑。
算法函数还有一个规律是具有两种后缀,
- 后缀_if 此后缀的函数一般有一个没有后缀的版本与之对应。如find和find_if,前者接受一个值,根据该值寻找容器中对应的元素,后者接受一个函数或函数对象(operator()必须返回bool,标识是否匹配)。
- 后缀_copy 此后缀用于将算法修改后的元素拷贝到一个新的容器中,原始容器不被修改,所以此算法需要更多的内存。
迭代器范围(Range)
STL的迭代器尊首一个原则:前闭后开,[first, last)。容器begin函数返回的迭代器表示容器中的第一个元素,而end函数返回的迭代器最后一个元素后面的位置(the one after the last element),也就是说*(end)没有意义,*(end-1)表示最后一个元素。这样有几个好处:1)统一标识容器结尾;2)计算迭代器距离时,不用额外加1。
示例
为什么要使用算法函数。然道不能用C++的基本语法完成同样的功能吗?答案是肯定的,算法库中的所有功能均可以使用最原始的C++语法实现,但是为什么要重复造轮子呢?而且,算法库提供而外的好处:1)代码简洁优雅,便于阅读和维护;2)大多数算法会比你实现的效率更高(由C++委员会的大牛们实现的,能不快吗?);3)更灵活,使用模版和迭代器风格,可以适配不同类型的数据类型和容器类型。
代码最优说服力,看看下面的例子吧!计算pearson系数,一种计算两个向量是否线性相关。取值范围[-1, 1],绝对值越大,越相关,-1代表线性递减,1代表线性递增,0代表线性无关。计算公式如下:
看看下面的代码:
#include <algorithm>
#include <numeric>
#include <vector>
#include <iostream>
#include <cmath>
using namespace std;
/**
* calculate person without STL style
*/
template<class T1, class T2>
double pearson(const vector<T1>& col1,const vector<T2>& col2) {
int n = col1.size();
double xy_sum = 0;
for(int i = 0; i < n; ++i) {
xy_sum += col1[i] * col2[i];
}
double x2_sum = 0;
for(int i = 0; i < n; ++i) {
x2_sum += pow(static_cast<double>(col1[i]),2);
}
double x_sum = 0;
for(int i = 0; i < n; ++i) {
x_sum += col1[i];
}
double y2_sum = 0;
for(int i = 0; i < n; ++i) {
y2_sum += pow(static_cast<double>(col2[i]),2);
}
double y_sum = 0;
for(int i = 0; i < n; ++i) {
y_sum += col2[i];
}
double deno = sqrt((x2_sum - 1.0 * pow(x_sum, 2) / n)*(y2_sum - 1.0 * pow(y_sum, 2) / n));
return (xy_sum - 1.0 * x_sum * y_sum / n)/ deno;
}
/**
* STL Style for pearson
*/
template<class InputIt1, class InputIt2>
double person_stl(InputIt1 firstX, InputIt1 lastX, InputIt2 firstY) {
int n = distance(firstX, lastX);
double xy_sum = inner_product(firstX, lastX, firstY, 0);
double x2_sum = inner_product(firstX, lastX, firstX, 0);
double y2_sum = inner_product(firstY, firstY + n, firstY, 0);
double x_sum = accumulate(firstX, lastX, 0);
double y_sum = accumulate(firstY, firstY + n, 0);
double deno = sqrt((x2_sum - 1.0 * pow(x_sum, 2) / n)*(y2_sum - 1.0 * pow(y_sum, 2) / n));
return (xy_sum - 1.0 * x_sum * y_sum / n)/ deno;
}
int main(int argc, char** argv) {
vector<int> col1,col2;
for (int i = 0; i < 10; ++i) {
col1.push_back(i);
col2.push_back(10-i);
}
cout << "Normal Style : " << pearson(col1,col2) << endl;
cout << "STL Style : " << person_stl(col1.begin(),col1.end(),col2.begin()) << endl;
return 0;
}
采用了两种方法实现了pearson系数,第一种采用的C++原始语法实现。第二种采用STL风格,可以看到前者用去了25行,而后者不到10行。
输出结果如下:
参考资料