遗传算法讲解与探讨
注: 遗传算法属于标准的随机算法,绝大多数随机算法比如退火算法、蚁群算法都有可以归结为遗传算法的一种特殊形式。本文是从通用的思想方式去讲解及探讨,更着重于如何理解完善该算法,而对算法具体实现方式,请参考相关文档。
绝大多数问题我们都可把其归结为状态空间的搜寻及选择的问题,通常我们的做法是逐一遍历所有的状态空间,进行比较选择得到最优值。比对一个找最大值的问题,下面就是其代码
for(int i=0;i<N;i++){
if(date[i]>Max)
Max=date[i];
}
思路就是对大小为N的状态空间就行遍历搜索。但很多时侯,状态空间N会是比较大,此时用这种方法,计算机也许几个世纪也得不到结果。比如较典型的一个NPC问题,巡回销售员问题(英文缩写为TSP问题),即要求在N个全连接的城市中找出一条距离最短的回路。这个问题的状态空间可以看作一个N维向量空间,每一个状态由N个值共同组成。如下图N=4时:
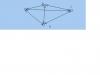
任何一个状态(即一个回路)可由Sa、Sb、Sc、Sd四个值构成,Sa可以在AB,AC,AD中任选一个,其它三个值也是类似。总的状态空间就是P(N-1)/2,当N很大时,我们就会考虑采用随机选择一些状态来进行尝试,
伪代码如下:
For(int i=0;i<nTryTimes;i++){
int pCity[N];//城市数组,每个城市从0到N编号
int n=0;//指定0号城市为起点城市
for(int j=1;j<N;j++){
while(IsSelected(n))//n被选过,则换一个
n=rand()%N;//随机选一个城市
pCity[j]=n;//指定n号声城市为下一要走的城市。
}
int nDistance=GetDistance(pCity);//获得该回路的距离
if(nDistance<Min)
Min=nDistance;
}
这种方法可以获得一个较优值,但不能保证得到的是最优值。
这就象买彩票一样,任何数都有可能会是大奖,没有规律可循,碰上大奖的机会是微乎其微的。实际上TSP问题和彩票问题是有一定区别的,彩票的状态解空间完全是随机分布的,而TSP问题的解空间则是有一定规律可寻的,最直观的一点就是一个状态值移动了一个城市的顺序后,得到的新状态的值和原状态的值是比较接近的,比如一个回路ABCDA,我们只移动B点的位置,改成回路ACBDA。二者的值是相对接近的(城市结点越多越明显),换句话说,就是解值相近的状态是按某一规则分布在一起的,这就为顺藤摸瓜的方式提供了可能。如果我们找到了一个较优值,那么顺着这个值按照某一演化规则,就可以找到若干和它相近的状态,只要原始状态的值越大,那么我们能够找到的大值状态的概率也就越大,也就是说新找到的这些状态中很可能就有更优一点的值,依次类推,我们就能逐渐的接近最优值。
整理一下刚才的解题思路,步骤如下:
1、先在状态空间中随机选取若干状态。
2、在这些状态中选出较优或合适的状态值。
3、以选中的状态值为基础,使用一些演化方式,演化到其它的状态,
4、重复2、3两个步骤直到获得满意的结果。
这就是遗传算法的基本思路。
只是在遗传算法中,不同的状态叫基因,演化方式有杂交方式(以两种状态为基础得到第三个状态),变异方式(只以一种状态为基础演化到其它状态),而第2步在遗传算法中就叫做优胜劣汰。
换一个思路来看,通常的遍历方式是以数组系列来进行的,从date[0]遍历到date[99],这种方式能够保证完全遍历,且不会重复,但是效率太差。遗传算法也是一种遍历方式,只是它的遍历不按序号来,首先是随机选,然后是基于已有的历史数据,并通过指定的规则得到新的数据,这种方式偏好性较强,对较优的状态会优先进行选择,这样效率就要高得多,找到最优值的机会也就更大,速度也更快。但是不可避免的会出现两个问题,
一是可能不能完全遍历,因为选择是有倾向的,就有可能即使给无限多的时间,也绝对不会选择到某些数据,而如果这些未被选的数据能够确定是次优的数据,则这是很有利的,但很多时侯我们并不能做出这个确认,这就会使我们错过了最优数据的选择,只能得到局部最优。
二是重复遍历的情况,会反复选择相同的一些数据,重复的选择带来的必然是效率的降低。
对应这两个问题的需要注意的也有两个方面:
一、如何选择、淘汰的问题。也就是选取哪些状态去演化,选择的依据是什么?选择的方式是什么。
比较典型的方法就是轮盘赌方法,这个方法能够保证会所有的数据都有被选中的机会。
二、演化的方式有哪些,如何选择演化方式?使用的演化方式如果进行无穷多次,能够保证会遍历到最优值吗?
我们的目的就是能够更快的获得最理想的值,而且当给定足够长(近于无穷)的时间情况下,理论上能保证一定能得到最优值。为了达到这个目标,就需要对状态空间的分布有一个深入的了解,发现的规律越多,越本质则我们越有可能获得最优值。


