Airbnb-Real-time Personalization using Embeddings for Search Ranking at Airbnb

Airbnb

Real-time Personalization using Embeddings for Search Ranking at Airbnb

Contributions

• Real-timr personalization（实时个性化）

• • 以前工作的个性化或者说是项目推荐都是通过离线生成user-item或者item-item表，然后在推荐的时候读取他们来部署到生产中。
  • 本文中实施了一个解决方案，就是用户最近与之交互的项目的embedding以在线的方式组合，以计算与需要排名的项目的相似度

• Adapting Training for Congregated Search （聚合搜索）

• • 旅游平台上的搜索通常是聚集的，用户只在某一个市场内进行搜索，例如Beijing，很少跨越不同的市场
  • 本文调整了嵌入训练算法以在进行负采样的时候考虑到这一点，从而获得更好的市场内列表相似性

• Leveraging Conversions as Global Context（利用转换作为全局上下文）

• • 将预定列表作为全局上下文

• User Type Embedding （用户类型嵌入）

• • 之前的工作捕捉用户长期兴趣的时候，为 每一个用户训练了一个单独的嵌入，但是，当目标比较稀疏的时候，没有足够的数据为用户训练出一个好的嵌入
  • 本文在用户类型级别训练嵌入，其中具有相同类型的用户将具有相同的嵌入

• Rejections as Explicit Negatives

• • 为了减少导致拒绝的推荐，本文将房源主拒绝视为负样本

Listing Embedding

Listing Embedding

\(S\) : a set of s click sessions obtained from N users

\(s = (l_1,...,l_m) \in S\) : each ession s is defined as un uninterrupted sequence of M listing ids that were clicked by the user

Aim:to learn d-dimensional real-valued representation \(v_{l_i}\in R^d\) of each unique listing \(l_i\),such that similar listing lie nearby in the embedding space.

\( v_l,v_l^{\prime}\) are the input and output vector representations of listing \(l\)

\(m\) hyperparameter is defined as a length of the relevant forward looking and backward looking context (neighborhood) for a clicked listing

\(V\) is a vocabulary defined as a set of unique listings ids in the data set

\[L = \sum_{s\in S}\sum_{l_i\in s}(\sum_{-m\geq j \leq m, i\neq0}\log P(l_{i+j}|l_i)) \]

\[P(l_{i+j}|l_i) = \frac{\exp)v_{l_i}^Tv_{l_{i+j}}^{\prime}}{\sum_{l=1}^{|V|}\exp(v_{l_i}^Tv_l^{\prime})} \]

To reduces computational complexity

\(D_p\) : a set of positive pairs (l,c) of cliked listings \(l\) and their contexts \(c\),(i.e. clicks on other listings by the same user that happened before and after click on listing l within a window of lengthm)

\(D_n\) : a set of negative pairs (l,c) of clicked listings and n randomly sampled listings from the entire vocabulary \(V\).

\[\arg \max _{\theta} \sum_{(l,c) \in D_p} \log{\frac{1}{1+e^{-v_c^{\prime}v_l}}} + \sum_{(l,c) \in D_n} \log{\frac{1}{1+e^{v_c^{\prime}v_l}}} \]

Booked Listing as Global Context

booked sessions & exploratory sessions

\(l_b\) is the embedding of the booked listing

\[\arg \max _{\theta} \sum_{(l,c) \in D_p} \log{\frac{1}{1+e^{-v_c^{\prime}v_l}}} + \sum_{(l,c) \in D_n} \log{\frac{1}{1+e^{v_c^{\prime}v_l}}} + \log{\frac{1}{1+e^{-v_{l_b}^{\prime}v_l}}} \]

As the window slides some listings fall in and out of the context set, while the booked listing always remains within it as global context (dotted line).

Adapting Training for Congregated Search

\(D_{m_n}\) a set of random negatives , sampled from the market of the central listing

\[\arg \max _{\theta} \sum_{(l,c) \in D_p} \log{\frac{1}{1+e^{-v_c^{\prime}v_l}}} + \sum_{(l,c) \in D_n} \log{\frac{1}{1+e^{v_c^{\prime}v_l}}} + \log{\frac{1}{1+e^{-v_{l_b}^{\prime}v_l}}} + \sum_{{l,m_n}\in D_{mn}} \log{\frac{1}{1+e^{v^{\prime}_{m_n}v_l}}} \]

Cold start listing embeddings

To create embeddings for new listings we propose to utilize existing embeddings of other listings.

Upon listing creation the host is required to provide information about the listing, such as location, price, listing type, etc. We use the provided meta-data about the listing to find 3 geographically closest listings (within a 10 miles radius) that have embeddings, are of same listing type as the new listing (e.g. Private Room) and belong to the same price bucket as the new listing (e.g. $20 − $25 per night). Next, we calculate the mean vector using 3 embeddings of identified listings to form the new listing embedding. Using this technique we are able to cover more than 98% of new listings

User-type & Listing-type Embdeeings

\(S_b\) : a set of booking sessions obtained from N users

\(s_b = (l_{b1},...,l_{bm})\) : a sequence of listing booked by user \(j\) ordered in time

Aim : to learn embedding \(v_{l_{id}}\) for each listing_id

Challenging

• First, booking sessions data \(S_b\) is much smaller than click sessions data \(S\) because bookings are less frequent events.
• Second, many users booked only a single listing in the past and we cannot learn from a session of length 1.
• Third, to learn a meaningful embedding for any entity from contextual information at least 5 − 10 occurrences of that entity are needed in the data, and there are many listing_ids on the platform that were booked less than 5 − 10 times.
• Finally, long time intervals may pass between two consecutive bookings by the user, and in that time user preferences, such as price point, may change, e.g. due to career change.

Training Procedure

\(S_b\) consisting of \(N_b\) booking sessions from N users

\(s_b \in (u_{type_1}l_{type_1},...,u_{type_M}l_{type_M}) \in S_b\) each session is defined as a sequence of booking events , i.e. \((user\_type,listing\_type)\)

\(D_{book}\) contains the user_type and listing_type from recent user history, specifically user bookings from near past and near future with respect to central item’s timestamp

\(D_{neg}\) contains random user_type or listing_type instances used as negatives.

For example, to update the central item which is a user_type (\(u_t\) ) we use

\[\arg \max_{\theta} \sum_{(u_t,c) \in D_{book}} \log{\frac{1}{1+e^{-v_c^{\prime}v_{u_t}}}} + \sum_{(u_t,c) \in D_{neg}} \log{\frac{1}{1+e^{v_c^{\prime}v_{u_t}}}} \]

Similarly, if the central item is a listing_type (\(l_t\) ) we optimize the following objective

\[\arg \max_{\theta} \sum_{(l_t,c) \in D_{book}} \log{\frac{1}{1+e^{-v_c^{\prime}v_{l_t}}}} + \sum_{(l_t,c) \in D_{neg}} \log{\frac{1}{1+e^{v_c^{\prime}v_{l_t}}}} \]

Explicit Negatives for Rejections

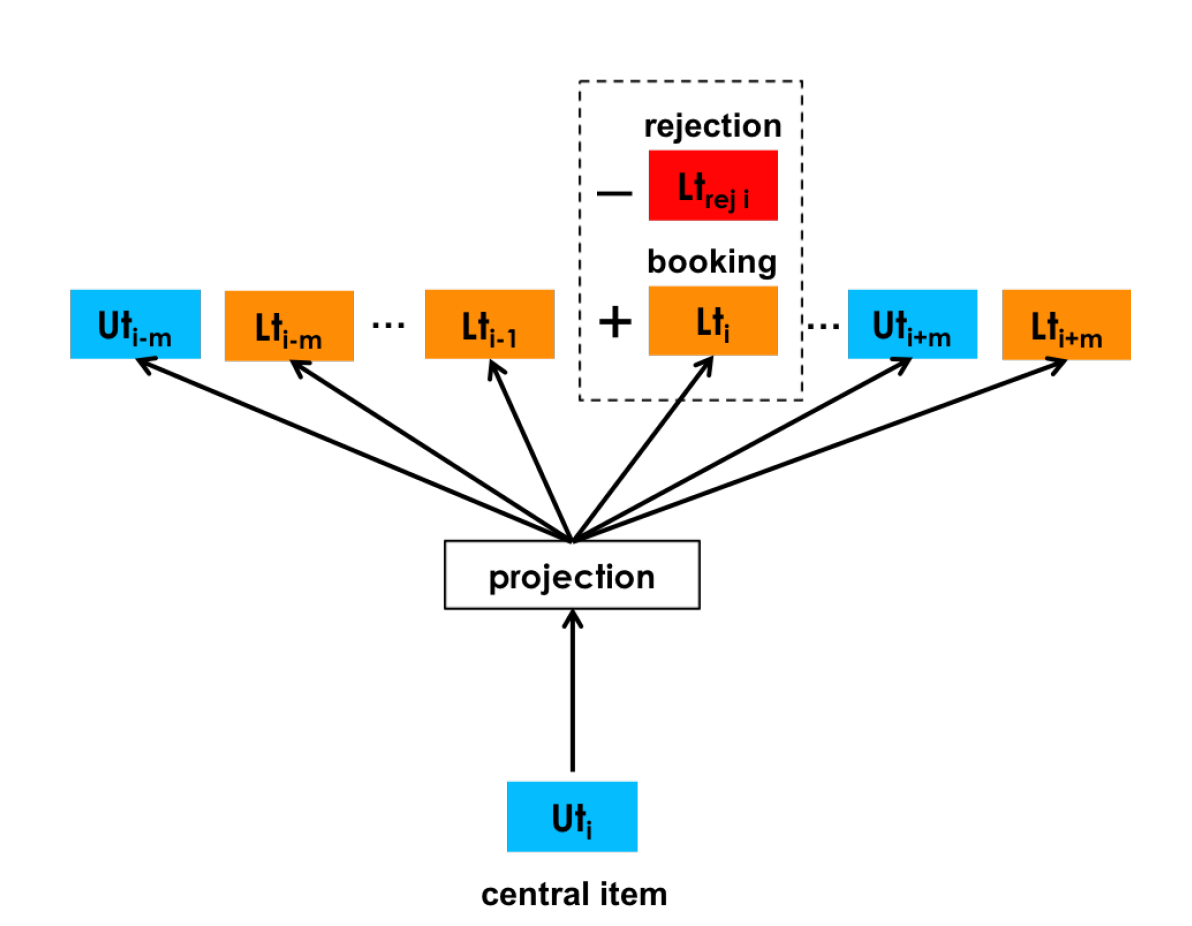
generate a set \(D_{reject}\)of pairs \((u_t , l_t )\) of user_type or listing_type that were involved in a rejection event.

\[\arg \max_{\theta} \sum_{(u_t,c) \in D_{book}} \log{\frac{1}{1+e^{-v_c^{\prime}v_{u_t}}}} + \sum_{(u_t,c) \in D_{neg}} \log{\frac{1}{1+e^{v_c^{\prime}v_{u_t}}}} + \sum_{(u_t,l_t)\in D_{reject}} \log{\frac{1}{1+\exp^{v^{\prime}_{l_t}v_{l_t}}}} \]

\[\arg \max_{\theta} \sum_{(l_t,c) \in D_{book}} \log{\frac{1}{1+e^{-v_c^{\prime}v_{l_t}}}} + \sum_{(l_t,c) \in D_{neg}} \log{\frac{1}{1+e^{v_c^{\prime}v_{l_t}}}} + \sum_{(u_t,l_t)\in D_{reject}} \log{\frac{1}{1+\exp^{v^{\prime}_{u_t}v_{l_t}}}} \]