chapter 15 DP

chapter 15 DP

写在最前

DP:dynamic programming (在这里programming指的是表格法，而并非计算机编写的程序)

书中例子

15.1 钢条切割

15.2 矩阵链乘法

15.3 最长公共子序列

15.4 最优二叉搜索树

思考题题

15.1 有向无环图中的最长简单路径

题目

给定一个有向无环图\(G=(V,E)\)，边权重为实数，给定图中两个顶点s和t。设计动态规划算法，求从s到t的最长加权简单路径，子问题图是什么样子的？算法的效率如何？

15.2 最长回文子序列

题目

回文(palindrome)是正序与逆序相同的非空字符串。例如，所有长度为1的字符串、civic、racecar、aibohphobia都是回文。设计高效算法，求给定输入字符串的最长回文子序列。例如，给定输入character，算法应该返回carac。算法的运行时间是怎样的？

15.3 双调欧几里得旅行商问题

题目

在欧几里得旅行商问题中，给定平面上 n n n个点作为输入，希望求出连接所有 n n n个点的最短巡游路线。下图(a)给出了一个7点问题的解。此问题是NP难问题，因此大家相信它并不存在多项式时间的求解算法（参见第34章）。J. L. Bentley建议将问题简化，限制巡游路线必须为双调巡游(bitonic tours)，即从最左边的点开始，严格向右前进，直至最右边的点，然后调头严格向左前进，直至回到起始点。下图(b)给出了相同7个点的最短双调巡游路线。问题简化之后，存在一个多项式时间的算法。

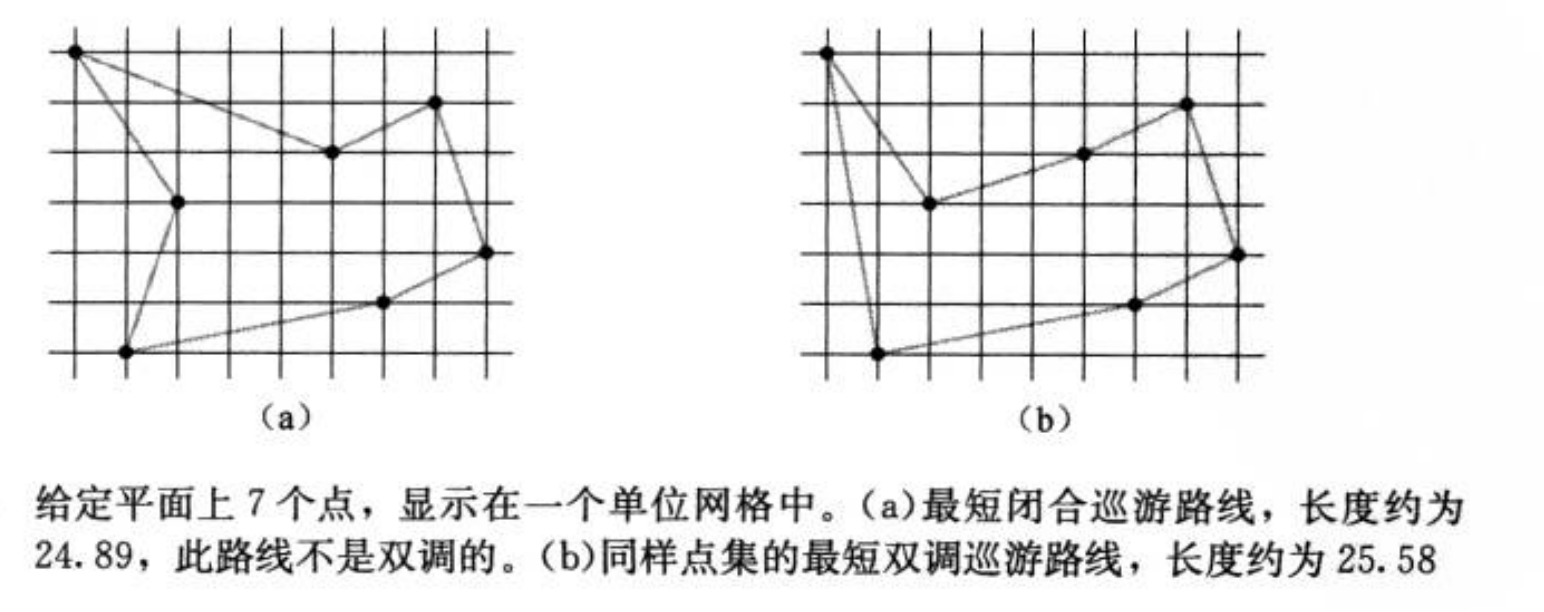
设计一个\(O(n^2)\)时间的最优双调巡游路线算法。你可以认为任何两个点的x坐标均不同，且所有实数运算都花费单位时间。（提示：由左至右扫描，对巡游路线的两个部分分别维护可能的最优解。）
15.3 双调欧几里得旅行商问题

15.4 整齐打印

题目

考虑整齐打印问题，即在打印机上用等宽字符打印一段文本。输入文本为n个单词的序列，单词长度分别为\(l_1,l_2,…,l_n\)个字符。我们希望将此段文本整齐打印在若干行上，每行最多M个字符。“整齐”的标准是这样的。如果某行包含从第i个到第j(i≤j)个的单词，且单词之间的间隔为一个空格符，则行尾的剩余空格符数量为\(M-j+i-\sum_{k=i}^{j}{l_k}\)，此值必须为非负的，否则一行无法容纳这些单词。我们希望能最小化所有行的（除最后一行外）剩余空格数的立方之和。设计一个动态规划算法，在打印机上整齐打印一段n个单词的文本。分析算法的时间和空间复杂度。

15.4 整齐打印

15.5 编辑距离

题目

为了将一个文本串\(x[1..m]\)转换为目标串\(y[1..n]\)，我们可以使用多种变换操作。我们的目标是，给定x和y，求将x转换为y的一个变换操作序列。我们使用一个数组z保存中间结果，假定它足够大，可存下中间结果的所有字符。初始时,z是空的；结束时，应有\(z[j]=y[j]，j=1,2,…,n\)。我们维护两个下标i和j，分别指向x和y中的位置，变换操作允许改变z的内容和这两个下标。初始时，\(i=j=1\)。在转换过程中应处理x的所有字符，这意味着在变换操作结束时，应当有\(i=m+1\)。我们可以使用如下6种变换操作：

• 复制(copy) — 从x复制当前字符到z，即进行赋值\(z[j]=x[i]\)，并将两个下标i和j都增1。此操作处理了\(x[i]\)。
• 替换(replace) — 将x的当前字符\(x[i]\)替换为另一个字符c，然后进行赋值\(z[j]=c\)，并将两个下标i和j都增1。此操作处理了\(x[i]\)。
• 删除(delete) — 删除x中的当前字符\(x[i]\)，即将i增1，j不变。此操作处理了\(x[i]\)。
• 插入(insert) — 将字符c插入z中,\(z[j]=c\)，将j增1，i不变。此操作未处理x中的字符。
• 旋转(twiddle，即交换) — 将x中的当前字符和下一个字符复制到z中，但交换顺序,\(z[j]=x[i+1]\)且\(z[j+1]=x[i]\)，将i和j都增2。此操作处理了\(x[i]\)和\(x[i+1]\)。
• 终止(kill) — 删除x中的剩余字符，令\(i=m+1\)。此操作处理了x中所有尚未处理的字符。如果执行此操作，则转换过程结束。
  　　下面给出了将源字符串algorithm转换为目标字符串altruistic的一种变换操作序列，下划线指出执行一个变换操作后两个下标i和j的位置：
  
  注意，还有其他方法将algorithm转换为altruistic。
  　　每个变换操作都有相应的代价。具体的代价依赖于特定的应用，但我们假定每个操作的代价是一个已知的常量。我们还假定复制和替换的代价小于删除和插入的组合代价，否则复制和替换操作就没有意义了。一个给定的变换操作序列的代价为其中所有变换操作的代价之和。在上例中，将algorithm转换为altruistic的代价为
  　　3•cost(copy)+cost(replace)+cost(delete)+4•cost(insert)+cost(twiddle)+cost(kill)
• a.给定两个字符串\(x[1..m]\)和\(y[1..n]\)以及变换操作的代价,x和y的编辑距离(editdistance)是将x转换为y的最小代价的变换操作序列的代价值。设计动态规划算法，求\(x[1..m]\)到\(y[1..n]\)的编辑距离，并打印最优变换操作序列。分析算法的时间和空间复杂度。

　　编辑距离问题是DNA序列对齐问题的推广。已有多种方法可以通过对齐两个DNA序列来衡量它们的相似度。有一种对齐方法是将空格符插入到两个序列x和y中，可以插入到任何位置（包括两端），使得结果序列x’和y’具有相同的长度，但不会在相同的位置出现空格符（即不存在j，使得x’[j]和y’[j]都是空格符）。然后为每个位置“打分”，位置j的分数为：
　　•+1，如果x’[j]=y’[j]且不是空格符
　　•−1，如果x’[j]≠y’[j]且都不是空格符
　　•−2，如果x’[j]或y’[j]是空格符
　　对齐方案的分数为每个位置的分数之和。例如，给定序列x=GATCGGCAT和y=CAATGTGAATC，一种对齐方案为

+表示该位置分数为+1，-表示分数为-1，*表示分数为-2，因此此方案的总分数为6•1 - 2•1 - 4•2 = -4。

• b. 解释如何将最优对齐问题转换为编辑距离问题，使用的操作为变换操作复制、替换、删除、插入、旋转和终止的子集。

a.

b.

15.6 公司聚会计划

题目

一位公司主席正在向Stewart教授咨询公司聚会的计划。公司的内部结构关系是层次化的，即员工按“主管─下属”关系构成一颗树，根结点为公司主席。人事部按“宴会交际能力”为每个员工打分，分值为实数。为了使所有参加聚会的员工都感到愉快，主席不希望员工及其直接主管同时出席。
　　公司主席向Stewart教授提供公司结构树，采用10.4节介绍的左孩子右兄弟表示法描述。树中每个结点除了保存指针外，还保存员工的名字和宴会交际评分。设计算法，求宴会交际评分之和最大的宾客名单。分析算法的时间复杂度。

15.7 译码算法

题目

15.8 基于接缝裁剪(seam carving)的图像压缩

题目

给定一幅彩色图像，它由一个\(m×n\)的像素数组\(A[1..m,1..n]\)构成，每个像素是一个红绿蓝(RGB)亮度的三元组。假定我们希望轻度压缩这幅图像。具体来说，我们希望从每一行中删除一个像素，使得图像变窄一个像素。但为了避免影响视觉效果，我们要求相邻两行中删除的像素必须位于同一列或相邻列。也就是说，删除的像素构成从顶端行到底端行的一条“接缝”(seam)相邻像素均在垂直或对角线方向上相邻。

• a. 证明：可能的接缝的数量是m的指数函数，假定\(n>1\)。
• b. 假定现在对每个像素\(A[i,j]\)，我们都已计算出一个实型的“破坏度”\(d[i,j]\)，表示删除像素\(A[i,j]\)对图像可视效果的破坏程序。
  直观地，一个像素的破坏度越低，它与相邻像素的相似度越高。再假定一条接缝的破坏度定义为它包含的像素的破坏度之和。设计算法，寻找破坏度最低的接缝。分析算法的时间复杂度。

a.
从第一行开始依次到最后一行选择删除点。第一行的删除点可以任意选择，即有n种选择。由于相邻两行的删除点也必须相邻，所以从第二行开始的每一行，删除点要么有2种选择，要么有3种选择，如下图所示。删除点有2种选择的情况出现在上一行的删除点为行首点或行末点的时候。

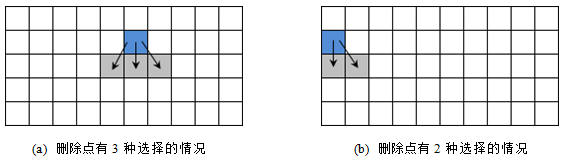
根据以上分析，采用计数原理即可得到一个\(m×n\)的图像的可能的接缝的数量在\(n•2^{m-1}\)和\(n•3^{m-1}\) 之间。所以，可能的接缝数量是m的指数函数。
b.
本题相对简单。用sd[i,j]sd[i,j]sd[i,j]表示以点[i,j][i,j][i,j]结尾的接缝的破坏度。以点[i,j][i,j][i,j]结尾的意思是，该条接缝只包含111~iii行，后面的行不考虑，并且第iii行的删除点是[i,j][i,j][i,j]。
　　对于一条以点[i,j][i,j][i,j]结尾的接缝，第i−1i-1i−1行的删除点有2种或3种选择。如果第i−1i-1i−1行的删除点有3种选择，那么删除点可以是[i−1,j−1][i-1,j-1][i−1,j−1]、[i−1,j][i-1,j][i−1,j]或[i−1,j+1][i-1,j+1][i−1,j+1]。从以第i−1i-1i−1行的这3个点结尾的接缝中选择破坏度最小的，再加上点[i,j][i,j][i,j]，即可得到以点[i,j][i,j][i,j]结尾的破坏度最小的接缝。再用link[i,j]link[i,j]link[i,j]表示第i−1i-1i−1行选择的是哪个点，−1-1−1表示选择[i−1,j−1][i-1,j-1][i−1,j−1]，000表示选择[i−1,j][i-1,j][i−1,j]，+1+1+1表示[i−1,j+1][i-1,j+1][i−1,j+1]。
　　第i−1i-1i−1行的删除点有2种选择的情况也可以做同样的分析。由此可以得到以下递归式。

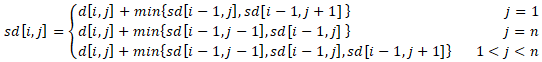
15.9 字符串拆分

题目

某种字符串处理语言允许程序员将一个字符串拆分为两段。由于此操作需要复制字符串，因此要花费n个时间单位来将一个n个字符的字符串拆分为两段。假定一个程序员希望将一个字符串拆分为多段，拆分的顺序会影响所花费的时间。例如，假定这个程序员希望将一个20个字符的字符串在第2个、第8个及第10个字符后进行拆分（字符由左至右，从1开始升序编号）。如果她按由左至右的顺序进行拆分，则第一次拆分花费20位时间单位，第二次拆分花费18个时间单位（在第8个字符处拆分字符串3~20），而第三次拆分花费12个时间单位。共花费50个时间单位。但如果她按由右至左的顺序拆分，第一次拆分花费20个时间单位，第二次拆分花费10个时间单位，第三次拆分花费8个时间单位，共花费38个时间单位。还可以按其他顺序，比如，她可以首先在第8个字符处进行拆分（时间20），接着在左边一段第2个字符处进行拆分（时间8），最后在右边一段第10个字符处进行拆分（时间12），总时间为40。
　　设计算法，对给定的拆分位置，确定最小代价的拆分顺序。更形式化地，给定一个n个字符的字符串S和一个保存\(m\)个拆分点的数组\(L[1..m]\)计算拆分的最小代价，以及最优拆分顺序。

如果整个字符串S[1..n]在第L[i]个字符(1≤i≤m)处被拆分，那么拆分下来的两个子串分别为S[1..L[i]]和S[L[i]+1..n]。假设一个子串是经由拆分得到的，它的左端是从原字符串的L[i]处拆分，它的右端是从原字符串的L[j]处拆分，其中1≤i<j≤m。那么，这个子串实际上为S[L[i]+1..L[j]]，并且这个子串的可选拆分点为L[i+1..j−1]。我们要对这个子串再行拆分，用sp[i,j]表示对这个子串首次拆分的拆分点在L中的索引，并用cost[i,j]表示对这个子串进行完全拆分所花费的时间。
　　上文提到，i和j的取值范围为1≤i<j≤m。为解决整个问题，需要对i和j的取值扩展一下。当i取值为0时，表示的子串为S[1..L[j]]；当j取值为m+1时，表示的子串为S[L[i]+1..n]。显然，当i=0并且j=m+1时，表示的子串实际上就是完整的字符串S[1..n]。我们最终要求解的就是i=0并且j=m+1的情况。相应地，我们要将拆分点数组L[1..m]也扩展一下，扩展为L[0..m+1]，其中L[0]=0，L[m+1]=n，其余数值保持不变。
　　我们现在求解一个子串的cost[i,j]。这个子串的长度为L[j]−L[i]，可选拆分点为L[i+1..j−1]。假设从L[k]处(i<k<j)进行拆分，那么cost[i,j]=L[j]−L[i]+cost[i,k]+cost[k,j]。我们遍历所有k的取值i<k<j，从中选取花费时间最小的。于是可以得到以下递归式。

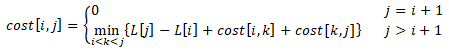
15.10 投资策略规划

题目

你所掌握的算法知识帮助你从Acme计算机公司获得了一份令人兴奋的工作，签约奖金1万美元。你决定利用这笔钱进行投资，目标是10年后获得最大回报。你决定请Amalgamated投资公司管理你的投资，该公司的投资回报规则如下。该公司提供n种不同的投资产品，从\(1~n\)编号。在第j年，第i种投资产品的回报率为\(r_{ij}\) 。换句话说，如果你在第j年在第i种投资产品投入d美元，那么在第j年年底，你会得到\(d·r_{ij}\)美元。回报率是有保证的，即未来10年每种投资产品的回报率均已知。你每年只能做出一次投资决定。在每年年底，你既可以将钱继续投入到上一年选择的投资产品中，也可以转移到其他投资产品中（转移到已有的投资产品，或者新的投资产品）。如果跨年时你不做投资转移，需要支付\(f_1\)美元的费用。否则，需要支付\(f_2\)美元的费用，其中\(f_2 \gt f_1\).

• a. 如上所述，本问题允许你每年将钱投入到多种投资产品中。证明：存在最优投资策略，每年都将所有钱投入到单一投资产品中（记住最优投资策略只需最大化10年的回报，无需关心任何其他目标，如最小化风险）。
• b. 证明：规划最优投资策略问题具有最优子结构性质。
• c. 设计最优投资策略规划算法，分析算法时间复杂度。
• d. 假定Amalgamated投资公司在上述规则上又加入了新的限制条款，在任何时刻你都不能在任何单一投资产品中投入15000美元以上。证明：最大化10年回报问题不再具有最优子结构性质。

a.
分三种情况。

• (1) 每一年都做投资转移
  这种情况下，显然每一年都应当选择回报率最大的那一款投资产品，才能使得10年总收益最大化。这里假设了每一年回报率最大的投资产品都不一样。
• (2) 每一年都不做投资转移
  假设每年都选择固定的一种投资产品。选择第1种投资产品的10年总收益为\(E_1\)​，选择第2种投资产品的10年总收益为\(E_2\)​，… …，选择第n种投资产品的10年总收益为\(E_n\)​。如果选择的是两种投资产品k1和k2，那么10年总收益必然是\(E_{k1}\)​与\(E_{k2}​的加权和，不会超过\)E_{k1}\(​与\)E_{k2}​中的较大者。因此，每年只选择一种投资产品所获得的总收益，不会比选择多种投资产品所获得的总收益要少。故在每一年都不做投资转移的情况下，每年只选择一种投资产品可以得到最大化收益。
• (3) 某些年份做投资转移，某些年份不做投资转移
  如果将连续不做投资转移的年份看做一个子问题，那么这个子问题属于情况(2)，在这些连续的年份之中都只选择一种投资产品，可以得到这个子问题的最大化收益。
  再将连续不做投资转移的年份合并为一个整体，我们可以将这个整体也当做一年。这样每一处有连续不做投资转移的年份都看做是一年。现在来看整个问题，其中的每一年都做了投资转移，这属于情况(1)。每一年都选择单一的投资产品也可得到最大化收益。
  综上所述，无论做不做投资转移，在每一年都选择单一的投资产品，10年后可以得到最大化收益。

b.
用e[i,j]表示在第j年选择第i种投资产品的前提下，前j年总的最大化收益。分析\(dp[i][j]\)需要考虑两种情况：

• 1. 第j年不做投资转移
     这种情况下，第j−1年也必须选择第i种投资产品。此时\(dp​_1[i][j]=(dp[i][j−1]−f_1​)⋅r_{ij}\)​。
• 2. 第j年做了投资转移
     这种情况下，第j−1年可以选择除i种之外的其他任意一种投资产品，显然我们要从中选择使得前j−1年总收益最大的那种投资产品。故\(dp_2​[i][j]=\max_{1<=k<= n \& k !=i} ​{(dp[k][j−1] −f_2​)⋅r_{ij}​}\)。

综合以上两种情况，dp[i][j]应当取二者中的较大值，即\(dp[i][j]=\max\{dp_1​[i][j],dp_2​[i][j]\}\)。我们还需用一个数组p[i][j]来保存第j−1年选择哪种投资产品。
从以上分析可以看出，规划最优投资策略问题具有最优子结构。因为求解第j年的最大化收益，依赖于第j−1年的最大化收益。

15.11 库存规划

题目

RinkyDink公司是一家制造溜冰场冰面修整设备的公司。这种设备每个月的需求量都在变化，因此公司希望设计一种策略来规划生产，需求是给定的，即它虽然是波动的，但是是可预测的。公司希望设计接下来n个月的生产计划。对第i个月，公司知道需求\(d_i\)即该月能够销售出去的设备的数量。令\(D = \sum_{i=1}^n d_i\)为后n个月的总需求。公司雇佣的全职员工，可以提供一个月制造m台设备的劳动力。如果公司希望一个月内制造多于m台设备，可以雇佣额外的兼职劳动力，雇佣成本为每制造一台机器付出美元。而且，如果在月末有设备尚未售出，公司还要付出库存成本。保存j台设备的成本可描述为一个函数 \(h(j)，j = 1,2,…,D\)。其中对所有 \(1 ≤ j ≤ D\)，满足 \(h(j) ≥ 0\)；对\(1≤j≤D−1\)，满足\(h(j)≤h(j+1)\)。
设计库存规划算法，在满足所有需求的前提下最小化成本。算法运行时间应为n和D的多项式函数。

状态定义：dp[i][j]:表示前i个月在总共生产j件商品的前提下的最小成本

状态转移方程

• if(i == 1)也就是第一天
  • \(if (j <= m)\),\(dp[i][j] = h(j-D_1)\)
  • \(if (j > m)\),\(dp[i][j] = h(j-D_1) + c(j-m)\)
• if (i> 1)
  • \(if(k<=m)\),\(\min_{0<=k<=j-D_{i-1}} {dp[i-1][j-k] + h(j-D_i)}\)
  • \(if(k>m)\),\(\min_{0<=k<=j-D_{i-1}} {dp[i-1][j-k] + h(j-D_i) + c(k-m)}\)

初始状态: i = 1

根据题意，有以下两点基本要求
1）要满足前n个月的总需求，那么n个月要生产D台设备
2）要满足前i个月的需求，那么前i个月生产的设备数量不能少于前i个月的需求之和

用\(dp[i][j]\)表示前i个月在总共生产j台设备下的最小成本。如果不考虑每一个月的需求，理论上j的取值范围是0-D，而i的取值范围是1-n。
用\(D_i\)表示前i个月的总需求,即\(D = \sum_{l=1}^id_l\)，显然有\(D_n = D\),假设第i个月选择生产k件设备，这意味着前i-1个月需要生产j-k台设备，第i个月的库存数量为\(j-D_i\)，相应的当月的库存成本是\(h(j-D_i)\),下面的动态规划递推公式中，\(j>=D_i\)并且\(j-k >= D_{i-1}\),也就是\(k<=j-D_{i-1}\)

\(if(k<=m)\),\(\min_{0<=k<=j-D_{i-1}} {dp[i-1][j-k] + h(j-D_i)}\)
\(if(k>m)\),\(\min_{0<=k<=j-D_{i-1}} {dp[i-1][j-k] + h(j-D_i) + c(k-m)}\)

我们还需要特别考虑一下\(i==1\)的情况。由于是第1个月，所以该月只能生产j台设备，此时\(dp[1][j]\)可按照下面步骤解决：
\(if (j <= m)\),\(dp[i][j] = h(j-D_1)\)
\(if (j > m)\),\(dp[i][j] = h(j-D_1) + c(j-m)\)

伪代码如下:

/**
params d : 保存了每一个月需求的数组
params m : 不额外雇佣劳动力的情况下，公司的每一个月的生产能力
params c : 额外雇佣劳动力生产一个产品的成本
return ： 返回一个数组，该数组保存了仅考虑前i个月并且生产设备总数为j的情况下，第i个月选择生产的设备数量的数组p
*/
public int[] inventoryPlay(int[] d,int m,int c){
	int n = d.length;
	int[] D = new int[n];
	D[1] = d[1];
	int maxD = D[1];
	for(int i = 2;i<n;i++){
		D[i] = D[i-1] + d[i];
		maxD = Math.max(maxD,D[i]);
	} 
	int[][] dp = new int[n][maxD];
	int[][] p = new int[n][maxD];
	// 对每一个月进行遍历
	for(int i = 1;i<n;i++){
		// 对生产的总的物品数量进行遍历，物品数量初始值从D_i开始 
		for(int j = D[i];j<maxD;j++){
			if(i==1){
				if(j<=m) dp[i][j] = h(j - D[i]);
				if(j>m) dp[i][j] = h(j-D[i]) + c(j-m);
			}
			else{
				dp[i][j] = Integer.MAX_VALUE;
				for(int k = 0;k<=j-D[i-1]]){
					int t = dp[i-1][j-k] + h(j-D[i]);
					if(k>m) t = t + c(k-m);
					if(t < dp[i][j]){
						dp[i][j] = t;
						p[i][j] = k;
					}
				}
			}
		}
	}
	return p;
}

15.12 签约棒球自由球员

题目

假设你是一支棒球大联盟球队的总经理。在寒季休季期间，你需要签入一些自由球员。球队老板给你的预算为X美元，你可以使用少于X美元来签入球员。但如果超支，球队老板就会解雇你。你正在考虑在N个不同位置签入球员，在每个位置上，有P个该位置的自由球员供你选择。由于你不希望任何位置过于臃肿，因此每个位置最多签入一名球员（如果在某个特定位置上你没有签入任何球员，则意味着计划继续使用现用球员）。为了确定一名球员的价值，你决定使用一种称为“VORP”或称为“球员替换价值”(Value Over Replacement Player)的统计评价指标(sabermetric),球员的VORP值越高，其价值越高。但VORP值高的球员的签约费用并不一定比VORP值低的球员高，因此还有球员价值之外的因素影响签约费用。
对每个可选择的自由球员，你知道他的三方面信息：

• 他打哪个位置
• 他的签约费用
• 他的VORP
  　　设计一个球员选择算法，使得总签约费用不超过X美元，而球员的总VORP值最大。你可以假定每位球员的签约费用是10万美元的整数倍。算法应输出签约球员的总VORP值、总签约费用，以及球员名单。分析算法的时间和空间复杂度。

本题要求预算为X美元的前提下签入N个不同位置的球员的最大化VORP值，用\(v[N,X]\)表示这个最大化VORP值。我们现在来提炼该问题的最优子结构。用\(v[i,x]\)表示预算为x美元\((0≤x≤X)\)的前提下从\(1 ~ i\)个不同位置\((1≤i≤N)\)签入球员的最大化VORP值。下面来建立v[i,x]的递归式。考虑第i个位置是否签入球员，分两种情况，用\(v_1​[i,x]\)和\(v_2​[i,x]\)分别表示两种情况下的最大化VORP值。
　　1) 第i个位置不签入球员
　　此时问题转化为预算仍然为x美元的前提下，从第1 ~ i−1个不同位置签入球员的最大化VORP值，即\(v_1​[i,x]=v[i−1,x]\)。
　　2) 第i个位置签入一个球员
　　用Si​[j]表示第i个位置的第j个球员(1≤j≤P)。如果从第i个位置签入第j个球员，该球员的签约费用和VORP值分别为\(S_i​[j].cost\)和\(S_i​[j].vorp\)，那么剩下的资金为\(x−S_i​[j].cost\)，我们接下来要用剩下的这些资金从1 ~ i−1个不同位置签入球员，即接下来要求解子问题\(v[i−1,x−S_i[j].cost]\)。此时总VORP值为\(S_i​[j].vorp+v[i−1,x−S_i​[j].cost]\)。当然，只有在满足\(S_i​[j].cost≤x\)
的条件下，才能从第i个位置签入第j个球员。由于每个位置最多只能签入一名球员，我们遍历从第i个位置签入任意一个球员的情况，从中选择总VORP值最大的情况。于是可以得到以下递归式。

求解过程中，我们用一个数组c[i,x]表示在求解v[i,x]时从第i个位置选择签入了哪个球员。如果c[i,x]=0，表示在第i个位置没有签入球员。