最长回文子序列
最长回文子序列
题目:给定一个字符串s,找到其中最长的回文子序列(注意,子序列跟子串是不一样的。子序列是从字符串中取出元素,相对顺序不变,但是可以不挨着。子串肯定是截取一段)
解法
- 递归
- 自顶向下的备忘录
- 自底向上的动态规划
- 状态定义:dp[i][j]表示s的第i个字符到第j个字符之间组成的子序列中,最长的回文子序列的长度是多少?
- 状态转移方程:(然后注意遍历顺序,i 从最后一个字符开始往前遍历,j 从 i + 1 开始往后遍历,这样可以保证每个子问题都已经算好了)
---> dp[i][j] = dp[i+1][j-1] +2; if s[i] == s[j]
---> dp[i][j] = max{dp[i+1][j] , dp[i][j-1]} ,else if s[i] != s[j]
- 初始化:dp[i][i] == 1
- 结果:dp[0][n-1]
动态规划求解的过程
All Coding
import java.util.*;
class Solution{
/**
给定一个字符串s,找到其中最长的回文子序列
注意,子序列跟子串是不一样的。子序列是从字符串中取出元素,相对顺序不变,但是可以不挨着。子串肯定是截取一段。
*/
public static void main(String[] args) {
String s = "bbbab";
System.out.println("-------------------");
System.out.println(lps1(s));
System.out.println("-------------------");
System.out.println(lps2(s));
System.out.println("-------------------");
System.out.println(lps3(s));
}
/**
递归
*/
public static int lps1(String s){
if(s == null || s.length() == 0) return 0;
int len = s.length();
char[] str = s.toCharArray();
return helper1(str,0,len-1);
}
public static int helper1(char[] str,int i,int j){
if(i==j) return 1;
if(i==j-1) return str[i] == str[j]?2:1;
if(str[i] == str[j]) return 2 + helper1(str,i+1,j-1);
else return Math.max(helper1(str,i,j-1),helper1(str,i+1,j));
}
/**
备忘录
*/
public static int lps2(String s){
if(s == null || s.length() == 0) return 0;
int len = s.length();
char[] str = s.toCharArray();
int[][] re = new int[len][len];
return helper2(str,0,len-1,re);
}
public static int helper2(char[] str,int i,int j,int[][] re){
if(re[i][j]!=0) return re[i][j];
if(i==j) return re[i][j] = 1;
if(i==j-1) return re[i][j] = str[i] == str[j]?2:1;
if(str[i] == str[j]) return re[i][j] = 2 + helper1(str,i+1,j-1);
else return re[i][j] = Math.max(helper1(str,i,j-1),helper1(str,i+1,j));
}
/**
dp,也就是自底向上
状态定义:dp[i][j]表示s的第i个字符到第j个字符之间组成的子序列中,最长的回文子序列的长度是多少?
状态转移方程:(然后注意遍历顺序,i 从最后一个字符开始往前遍历,j 从 i + 1 开始往后遍历,这样可以保证每个子问题都已经算好了。)
dp[i][j] = dp[i+1][j-1] +2; if s[i] == s[j]
dp[i][j] = max{dp[i+1][j] , dp[i][j-1]} ,else if s[i] != s[j]
初始化:dp[i][i] == 1
结果:dp[0][n-1]
*/
public static int lps3(String s){
if(s==null || s.length() == 0) return 0;
int len = s.length();
char[] str = s.toCharArray();
int[][] dp = new int[len][len];
for(int i = len-1;i>=0;i--){
dp[i][i] = 1;
for(int j = i+1;j<len;j++){
if(str[i] == str[j]) dp[i][j] = dp[i+1][j-1] +2;
else dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][len-1];
}
}
Saying Less Doing More


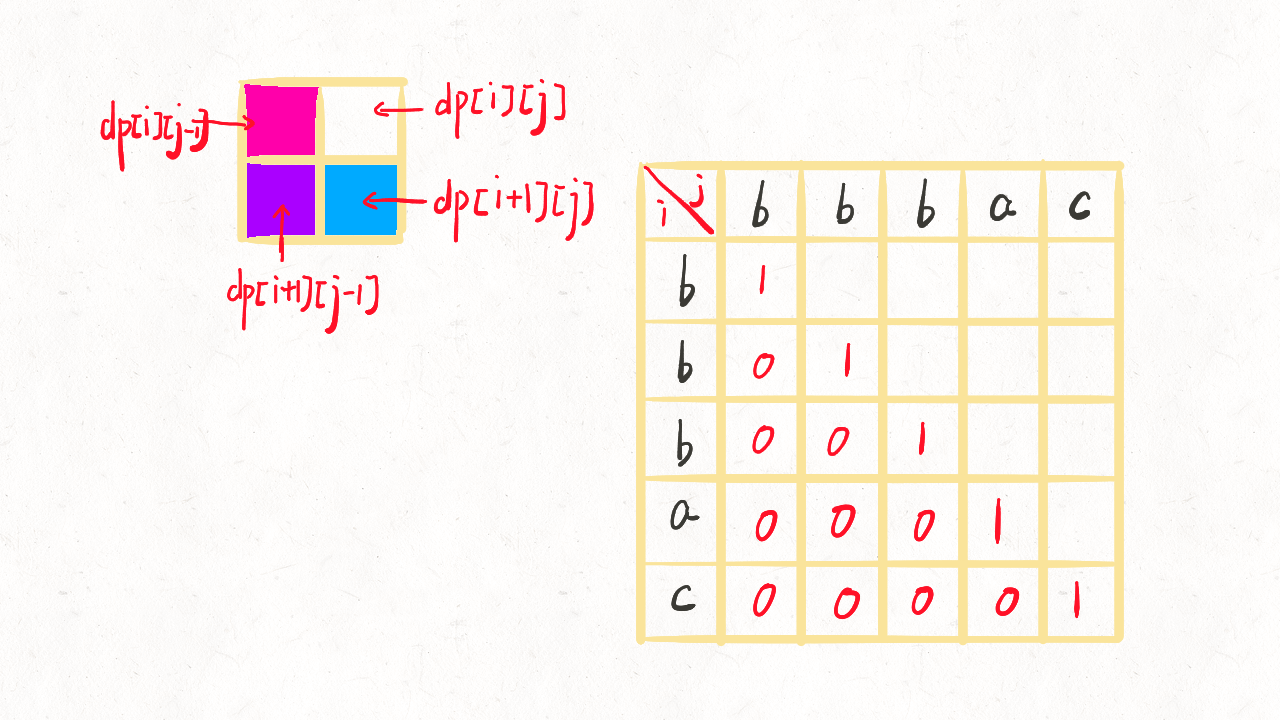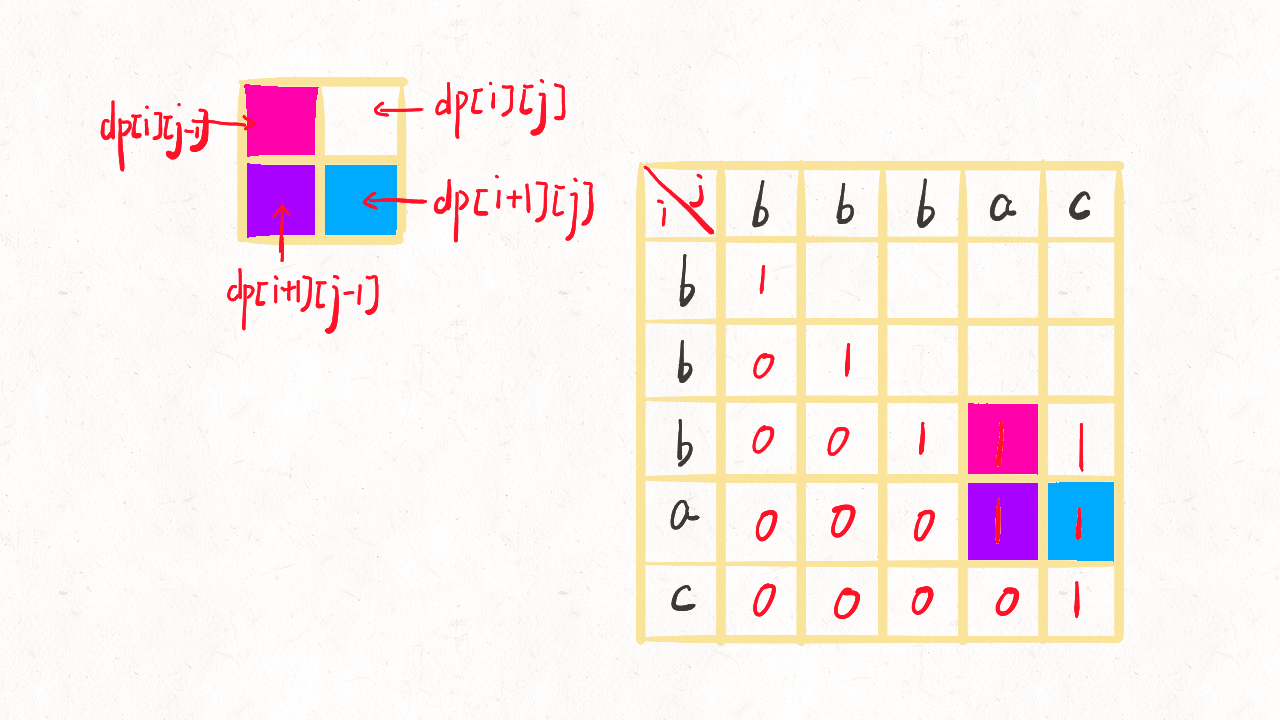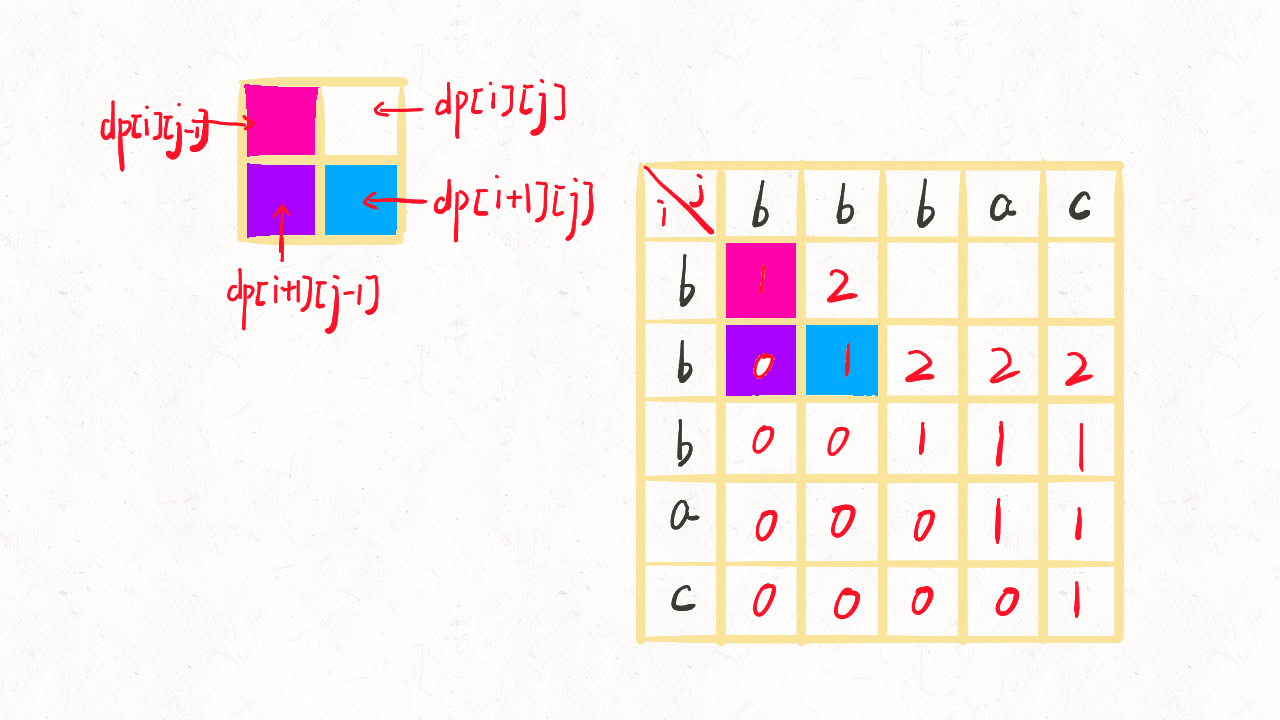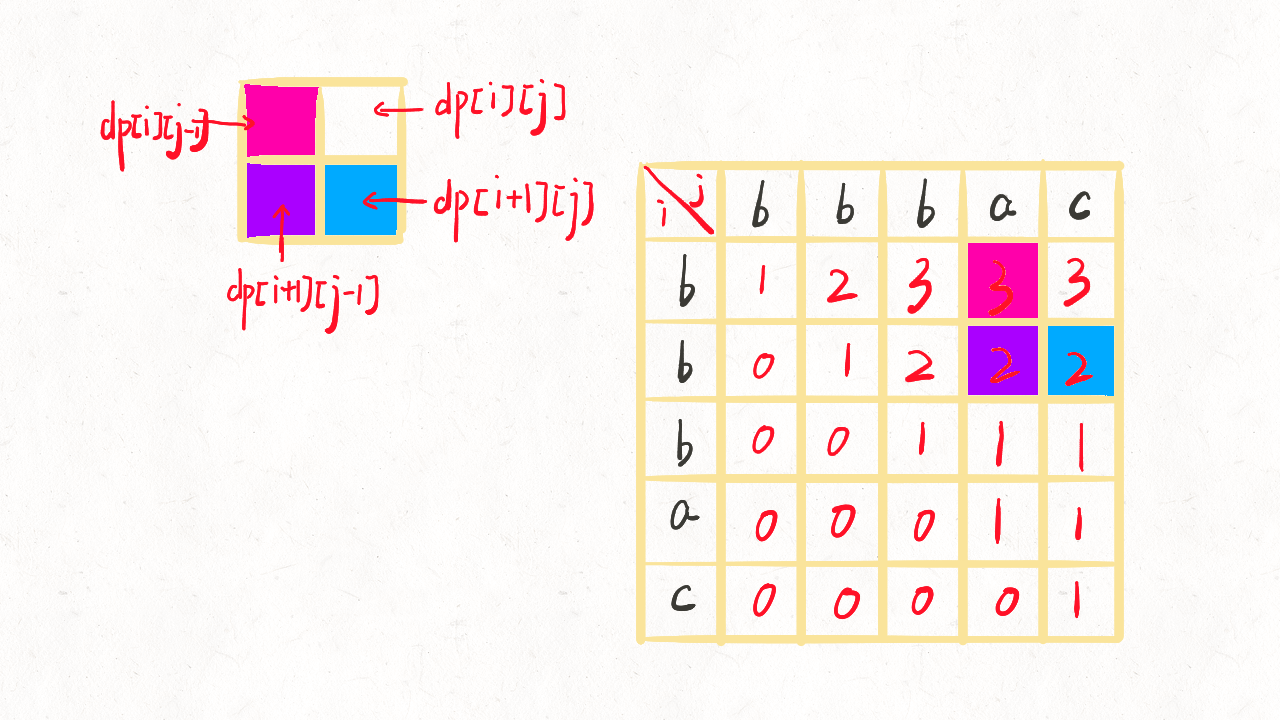

 浙公网安备 33010602011771号
浙公网安备 33010602011771号