cutRod

cutRod问题

问题：有一根铁条，不同的长度收益不同，求如何切割，可以让铁条的收益最大,铁条的收益与长度的对应关系如下表所示

length	0	1	2	3	4	5	6	7	8	9	10
profit	0	1	5	8	9	10	17	17	20	24	30

解决方案

• 递归
  分成子问题，例如4可以分为2+2，3+1，0+4，1+3，1+1+1+1，1+1+2
• 自顶向下的备忘录算法
  此方案仍然按照自然的递归形式编写整体的流程，但是呢，不同的是，在执行的过程中会保存每一个子问题的解（通常保存在一个数组中），当需要一个子问题的解的时候，首先会检查是否已经保存过此解。如果是，则就直接返回保存的数组中的值，如果不是，按照通常的方式解决此问题即可。
• 自底向上法
  这种方法一般需要恰当定义子问题的规模的概念，使得任何子问题都依赖于更小的子问题的求解。因而我们可以将子问题按规模排序，并且按照由小到大排序，当求解某一个问题的时候，其子问题已经被解决，并且每一个子问题就保存计算一次。
  - 状态定义：dp[i] 表示当铁条长度为i的时候的最大收益
  - 状态转移方程:dp[i] = Math.max(dp[i],p[j] + dp[i-j]) for j = 1 to i 表示从[i-j]的长度转移而来
  - 初始状态:dp[0] = 0 表示铁条的长度为0的时候，最大收益为0
• 自底向上并记录转移过程

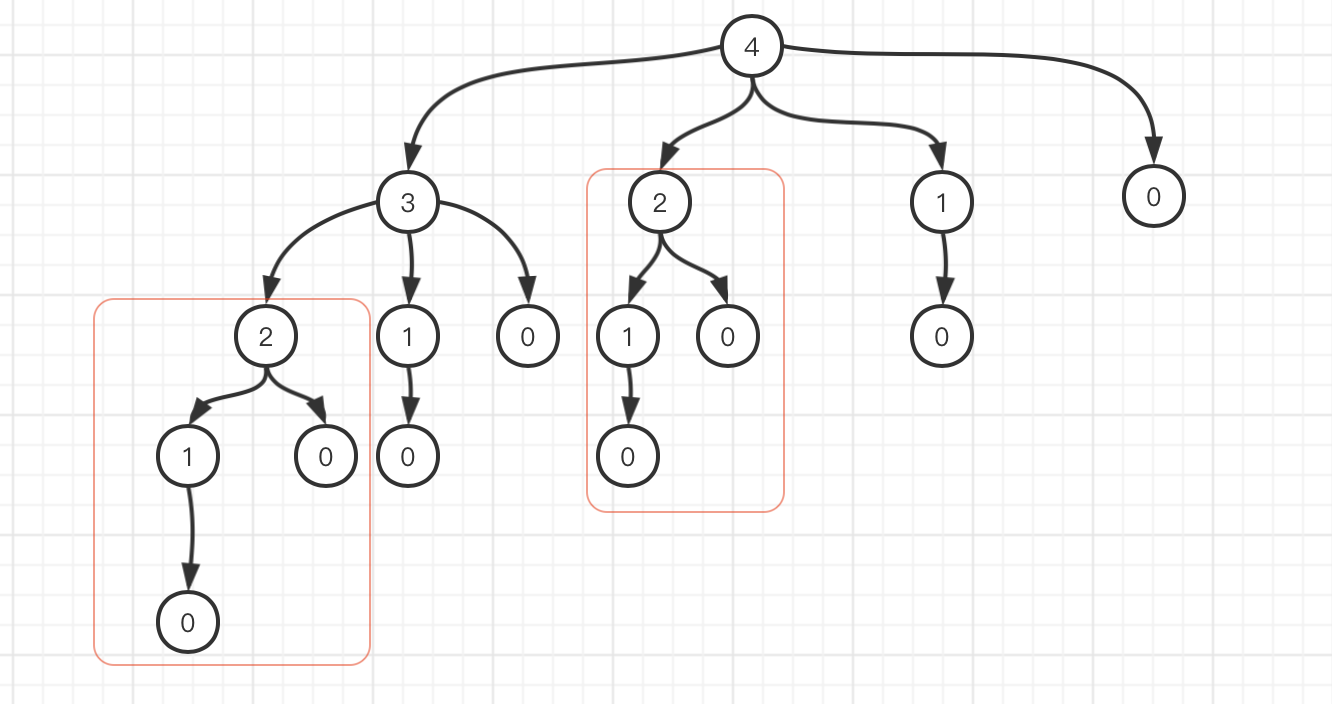
为什么递归会有重复计算？（以长度为4的铁条为例子）

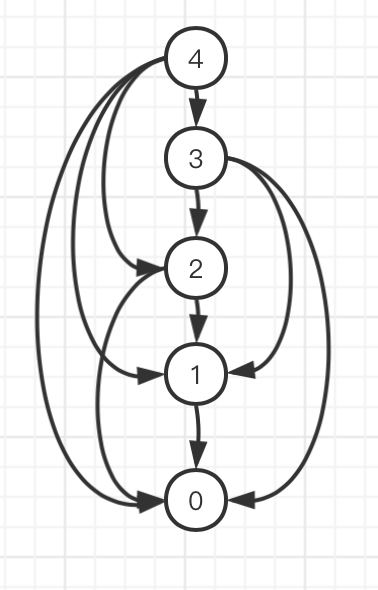
针对于动态规划的（也就是自底向上的方法的）子问题图

All Coding

import java.util.*;
class Solution{
	/**
	问题：有一根铁条，不同的长度收益不同，求如何切割，可以让铁条的收益最大
	铁条的收益与长度的对应关系如下表所示
	|length|0|1|2|3|4|5|6|7|8|9|10|
	|---|---|---|---|---|---|---|---|---|---|---|----|
	|profit|0|1|5|8|9|10|17|17|20|24|30|
	*/
	static int[] p = new int[]{0,1,5,8,9,10,17,17,20,24,30};
	static int[] r = new int[p.length];
	public static void main(String[] args) {
		Arrays.fill(r,Integer.MIN_VALUE);
		System.out.println("--------------------");
		System.out.println(cutRod(p,10));
		System.out.println("--------------------");
		System.out.println(memoizedCutRod(p,10,r));
		System.out.println("--------------------");
		System.out.println(bottomUpCutRod(p,10));
		System.out.println("--------------------");
		System.out.println(bottomUpCutRod2(p,7));
	}
	/**
	params:int[] p : 价格数组
	params:int n : 长度
	function：返回长度为n的钢条的最大收益
	方法：递归
	分成子问题，例如4可以分为2+2，3+1，0+4，1+3，1+1+1+1，1+1+2

	*/
	public static int cutRod(int[] p , int n){
		if(n == 0) return 0;
		int q = Integer.MIN_VALUE;
		for(int i = 1;i<=n;i++){
			q = Math.max(q,p[i] + cutRod(p,n-i));
		}
		return q;
	}
	/**
	带备忘录的自顶向下方法
	此方案仍然按照自然的递归形式编写整体的流程，但是呢，不同的是，在执行的过程中会保存每一个子问题的解（通常保存在一个数组中），当需要一个子问题的解的时候，首先会检查是否已经保存过此解。
	如果是，则就直接返回保存的数组中的值，如果不是，按照通常的方式解决此问题即可。
	params:int[] p : 价格数组
	params:int n : 长度
	params:int[] r : 备忘录record
	*/
	
	public static int memoizedCutRod(int[] p,int n,int[] r){
		if(r[n] >= 0) return r[n];
		if(n==0) return 0;
		int q = Integer.MIN_VALUE;
		for(int i = 1;i<=n;i++){
			q = Math.max(q,p[i] + memoizedCutRod(p,n-i,r));
		}	
		r[n] = q;
		return q;

	}
	/**
	自底向上方法
	这种方法一般需要恰当定义子问题的规模的概念，使得任何子问题都依赖于更小的子问题的求解。因而我们可以将子问题按规模排序，并且按照由小到大排序，当求解某一个问题的时候，其子问题已经被解决，并且每一个子问题就保存计算一次。
	状态定义：dp[i] 表示当铁条长度为i的时候的最大收益
	状态转移方程:dp[i] = Math.max(dp[i],p[j] + dp[i-j]) for j = 1 to i 表示从[i-j]的长度转移而来
	初始状态:dp[0] = 0 表示铁条的长度为0的时候，最大收益为0
	*/
	public static int bottomUpCutRod(int[] p,int n){
		int[] dp = new int[p.length];
		dp[0] = 0;
		for(int j = 1;j<=n;j++){
			int q = Integer.MIN_VALUE;
			for(int i =1;i<=j;i++){
				q=Math.max(q,p[i] + dp[j-i]);
			}
			dp[j] = q;
		}
		return dp[n];

	}
	/**
	自底向上方法并且记录转移过程
	*/
	public static int bottomUpCutRod2(int[] p,int n){
		int[] dp = new int[p.length];
		// 数组s用来记录转移过程
		int[] s = new int[p.length];
		dp[0] = 0;
		for(int j = 1;j<=n;j++){
			int q = Integer.MIN_VALUE;
			for(int i =1;i<=j;i++){
				if(q < p[i] + dp[j-i]){
					q = p[i]+dp[j-i];
					s[j] = i;
				}
			}
			dp[j] = q;
		}
		int t = n;
		while(t>0){
			System.out.print(s[t]+" ");
			t-=s[t];
		}
		System.out.println();
		return dp[n];
	}
}