1.13 NIM(3)两堆石头的游戏

1.13 NIM(3)两堆石头的游戏

基本问题：假设有两堆石子，两人轮流取石子，每次可以从一堆取任意个石子，或者从两堆取相等数量的任意个石子，但不能不取。若先把石子取光的一方为胜方，先取者有什么必胜策略？

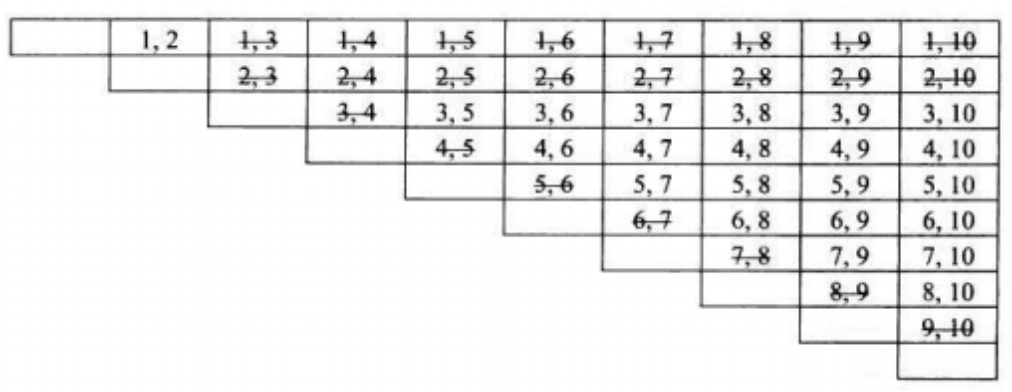
解题思路：参考质数筛子法，先列举（10，10）所可能的情况，筛选掉所有安全局面（先取者必胜称为“安全局面”，反之为“不安全局面”）

得到如下的递推式：
首先\((1,2)\)是一个安全局面，目标就是寻找所有的安全局面。

\[a_1 = 1,b_1 = 2 \]

\[an为未出现在2n-2内的最小整数 \]

\[b_n = a_n + n \]

通项公式为:

\[an=[a * n] , bn=[b * n] , a= \frac{1 + \sqrt{5}} {2} b=\frac{3 + \sqrt{5}}{2} \]