4.11 挖雷游戏的概率

4.11 挖雷游戏的概率

基本题目 用户的第一次点击不会碰到任何地雷，程序在此之后随机放地雷。第二次点击的时候要小心了，可能遇雷身亡。这个游戏局面一共有16*16=256个方块，P(A),P(B),P(C)代表位置A,B,C中是地雷的概率，求此概率？

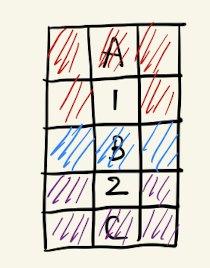
• 有两个雷的情况 \(C_{M-15}^{N-2}*C_3^1*C_5^1\),其中\(C_3^1\)是蓝色区域中的概率，\(C_5^1\)是紫色区域中的概率
  A处为雷的概率：\(0\)
  B处为雷的概率：\(C_{M-15}^{N-2}*1*C_5^1\)
  C处为雷的概率：\(C_{M-15}^{N-2}*C_3^1*1\)
• 有三个雷的情况\(C_{M-15}^{N-3}*C_5^1*C_5^2\),其中\(C_5^1\)是红色区域中的概率，\(C_5^2\)是紫色区域中的概率
  A处为雷的概率：\(C_{M-15}^{N-3}*1*C_5^2\)
  B处为雷的概率：\(0\)
  C处为雷的概率：\(C_{M-15}^{N-3}*C_5^1*C_4^1\)

总结：

\[P(A) = \frac{10*C_{M-15}^{N-3}}{15*C_{M-15}^{N-2} + 50*C_{M-15}^{N-3}} \]

\[P(A) = \frac{5*C_{M-15}^{N-2}}{15*C_{M-15}^{N-2} + 50*C_{M-15}^{N-3}} \]

\[P(A) = \frac{3*C_{M-15}^{N-2} + 20 * C_{M-15}{N-3}}{15*C_{M-15}^{N-2} + 50*C_{M-15}^{N-3}} \]