3.3 计算字符串的相似度

3.3 计算字符串的相似度

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

解法1

采用递归的方法进行计算
思想分析：重点是转化成为子问题的过程
s1[1,10] s2[1,10]
如果字符串s1的第1个字符与s2的第一个字符相同，那么距离为0，再去判断s1的第二个字符与s2的第二个字符
如果字符串s1的第i个字符与s2的第i个字符不相同，那么距离+1，我们可能可以通过以下方式更改：
	1，将s1的第i个删除，然后计算s1[i+1,10]与s2[i,10]的距离
	2，将s2的第i个删除，然后计算s1[i,10]与s2[i+1,10]的距离
	3，将s1的第i个字符修改成为s2的第i个字符，然后计算s1[i+1,10]与s2[i+1,10]的距离
	4，将s2的第i个字符修改称为s1的第i个字符，然后计算s1[i+1,10]与s2[i+1,10]的距离
	5，增加一个字符到s1的第i个元素之前，然后计算s1[i,10]与s2[i+1,10]的距离
	6，增加一个字符到s2的第i个元素之前，然后计算s1[i+1,10]与s2[i,10]的距离
但是值得注意的是，我们应该关注
	1，一步操作之后，将s1[i+1,10]与s2[i,10]变成相同字符串
	2，一步操作之后，将s1[i,10]与s2[i+1,10]变成相同字符串
	3，一步操作之后，将s1[i+1,10]与s2[i+1,10]变成相同字符串

class Test{
	public static void main(String[] args) {
		String s1 = "abc";
		String s2 = "cba";
		System.out.println(calculateStringDistance(s1,0,s1.length()-1,s2,0,s2.length()-1));
		System.out.println(calculateStringDistance2(s1,s2));

	}
	public static int calculateStringDistance(String s1,int start1,int end1,String s2,int start2,int end2){
		if(start1 > end1){
			if(start2 > end2) return 0;
			else return end2 - start2 + 1;
		}
		if(start2 > end2){
			if(start1 > end1) return 0;
			else return end1 - start1 + 1;
		}
		if(s1.charAt(start1) == s2.charAt(start2)) return calculateStringDistance(s1,start1+1,end1,s2,start2+1,end2);
		else{
			int t1 = calculateStringDistance(s1,start1,end1,s2,start2+1,end2);
			int t2 = calculateStringDistance(s1,start1+1,end1,s2,start2,end2);
			int t3 = calculateStringDistance(s1,start1+1,end1,s2,start2+1,end2);
			return Math.min(t1,Math.min(t2,t3))+1;
		}
	}
}

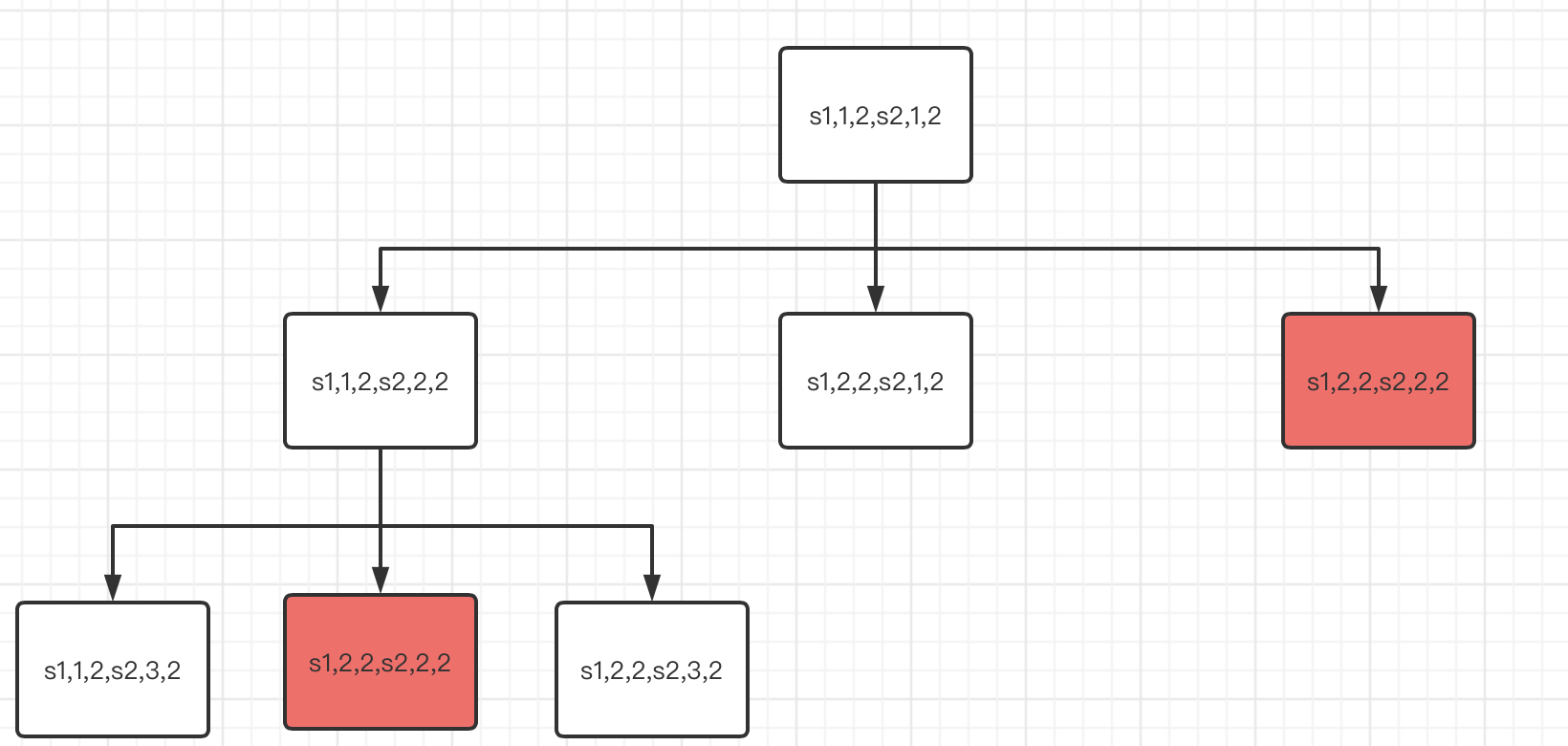
解法1的问题如下图，重复计算,重点看两个红色节点

解法2:动态规划

状态定义：
	dp[i][j] 表示s1的前i个字符和s2的前j个字符之间的距离
状态转移方程：
	if s1和s2的最后一个字母相同
		dp[i][j] = min{dp[i][j-1] +1 ,dp[i-1][j] + 1,dp[i-1][j-1]}
	if s1和s2的最后一个字母不同
		dp[i][j] = min{dp[i][j-1] + 1,dp[i-1][j] + 1,dp[i-1][j-1] + 1}
初始化定义：
	dp[i][0] = i
	dp[0][j] = j 

class Test{
	public static void main(String[] args) {
		String s1 = "abc";
		String s2 = "cba";
		System.out.println(calculateStringDistance(s1,0,s1.length()-1,s2,0,s2.length()-1));
		System.out.println(calculateStringDistance2(s1,s2));

	}
	public static int calculateStringDistance2(String s1,String s2){
		int n = s1.length();
		int m = s1.length();
		if(n * m == 0) return n+m;
		int[][] dp = new int[n+1][m+1];
		// 边界初始化
		for(int i = 0;i<n+1;i++) dp[i][0] = i;
		for(int j = 0;j<m+1;j++) dp[0][j] = j;
		for(int i = 1;i<n+1;i++){
			for(int j = 1;j<m+1;j++){
				if(s1.charAt(i-1) == s2.charAt(j-1)) dp[i][j] = Math.min(Math.min(dp[i][j-1] + 1,dp[i-1][j] +1),dp[i-1][j-1]);
				else dp[i][j] = Math.min(Math.min(dp[i-1][j] + 1,dp[i][j-1] + 1),dp[i-1][j-1]+1);
			}
		}
		return dp[n][m];
	}
}