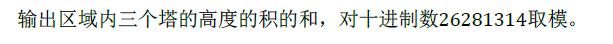题解 DTOJ #1515.三塔合一
欢迎访问 My Luogu Space。
【题目描述】
【输入输出格式】
输入格式:
输出格式:
【输入输出样例】
输入样例:
5 1 1 2 2
输出样例:
643
【标签】
模拟,数学推演。
【分析】
考虑通过发现规律来简化计算。
基本想法:
从题目中可以发现,第二、三座塔对应格子的乘积可以化成平方差,而每个格子的被减的平方项就是当前所在的层(每一圈算作一层)的右下角的值的平方,减数则是从右下角顺时针或者逆时针前进到达当前格子所用的步数(左上角的格子需单独处理)。
因此,从每层的左下角出发顺时针或者逆时针前进,直到左上角之前所经过的位置的二、三座塔的乘积之和为 \(\sum_{i=0}^{s}p^2-i^2\) ,其中 \(p\) 为当前层的右下角的值,\(s\) 为走到当前位置需要用的步数。
改进:
由于本题所被发现的性质依赖每一层的左下角的格子的值,因此本题可以通过“右下缀和”来更方便地计算答案。
通过一个值 \(c\) 来维护当前层的左下角格子的值( \(c\) 可找规律),并从最外层开始一层一层往内统计,每层都顺时针和逆时针走到不能走为止,最后将答案相加取模即可(还有第一层塔不能忽略,并且右下角的格子会被计算两次需要去掉一次或单独计算)。
每层的值可以化成 \(k*(s*p^2-\sum\limits_{i=0}^{s}i^2)\),其中 \(k\) 为第一座塔对应的值 (每一层对应的第一座塔的值是相等的),而 \(\sum\limits_{i=0}^{s}i^2\) 为平方数列前 \(n\) 项和,可通过公式 \(\frac{n*(n+1)*(2n+1)}{6}\) 来计算。
【代码】
[C++]
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const LL Mod = 26281314;
LL n, X1, Y1, X2, Y2;
LL Do(LL X){return X*(X+1)/2*(2*X+1)/3%Mod;} //计算平方数列前n项和
LL Work(LL X, LL Y){
LL r=n, mid=n/2+1, sum=0, c=1; //c维护每层的右下角值与左上角值
while(r>=X && r>=Y && r>=mid){ //从最外层往内统计
LL s1=0, s2=0, l=n-r+1; //s1、s2为步数,l为当前层的左上角的横纵坐标(横纵坐标相等)
if(l==r){ //当到达最中心一格时
sum += c%Mod*c%Mod*r%Mod;
sum %= Mod;
break;
}
if(Y<=l){ //能向上走到底
s1 += r-l;
if(X<=l) s1 += r-l-1; //能向左走到底
else s1 += r-X;
}
else s1 += r-Y;
if(X<=l){ //能向左走到底
s2 += r-l;
if(Y<=l) s2 += r-l-1; //能像上走到底
else s2 += r-Y;
}
else s2 += r-X;
if(X<=l && Y<=l){ //能走到左上角的格子
sum += c*l%Mod*c;
sum %= Mod;
}
c += (n-(n-r)*2-1)*2; //变为右下角的值
c %= Mod;
sum = ((sum+l*s1%Mod*c%Mod*c%Mod-Do(s1)*l%Mod+Mod)%Mod+Mod)%Mod;
sum = ((sum+l*s2%Mod*c%Mod*c%Mod-Do(s2)*l%Mod+Mod)%Mod+Mod)%Mod;
sum = (sum+l*c%Mod*c%Mod)%Mod; //统计上右下角的值
c += (n-(n-r)*2-1)*2; //变为下一层左上角的值
c %= Mod;
r--;
}
return sum;
}
int main(){
cin>>n>>X1>>Y1>>X2>>Y2;
LL ans = Work(X1, Y1);
ans = (ans-Work(X1, Y2+1)+Mod)%Mod; //“右下缀和”
ans = (ans-Work(X2+1, Y1)+Mod)%Mod;
ans = (ans+Work(X2+1, Y2+1))%Mod;
cout<<ans<<endl;
return 0;
}
【补充】
记得随时取模,多取模,拼命地取模!