Leetcode#84 Largest Rectangle in Histogram

原题地址

 

有两种方法，左右扫描或辅助栈。

方法I： 左右扫描法
考虑到最大面积的矩形高度一定跟某个条一样高，所以挨个枚举每个条，看其向左、向右最多能延伸到多远。在计算左右边界时，可以借助之前计算过的结果迭代（类似动归的感觉）优化以减少时间复杂度，这应该算是唯一的难点了。总的来说，向左一遍，向右一遍，整体求面积再一遍，一共需要3次遍历，时间复杂度是O(n)。

左右扫描法非常直观。

代码：

    int largestRectangleArea(vector<int> &height) {
        if (height.empty()) return 0;

        int n = height.size();
        int maxArea = 0;
        int *left = new int[n]; // 向左能延伸多远
        int *right = new int[n]; // 向右能延伸多远

        // 向右延伸
        right[n - 1] = 1;
        for (int i = n - 2; i >= 0; i--) {
            if (height[i] > height[i + 1])
                right[i] = 1;
            else {
                int j = i + 1;
                while (j < n && height[j] >= height[i])
                    j += right[j];
                right[i] = j - i;
            }
        }

        // 向左延伸
        left[0] = 1;
        for (int i = 1; i < n; i++) {
            if (height[i] < height[i - 1])
                left[i] = 1;
            else {
                int j = i - 1;
                while (j >= 0 && height[j] >= height[i])
                    j -= left[j];
                left[i] = i - j;
            }
        }

        // 求面积
        maxArea = height[0];
        for (int i = 0; i < n; i++) {
            maxArea = max(height[i] * (left[i] + right[i] - 1), maxArea);
        }

        return maxArea;
    }

 

 

方法II： 辅助栈法（网上很多人采用的方法）

根本思想是：依次遍历所有矩形条，尝试计算以该矩形条为高度的矩形面积。但是在遍历的时候我们不知道后面还有什么样的矩形条怎么办？没关系，对于没法确定面积的矩形，压栈，留着以后处理，而对于那些已经可以确定计算出面积的矩形条，留着也没用，弹栈。

如果我们能知道一个矩形条向左向右最远能延伸多远，我们就能计算出以该矩形条为高的矩形面积了！我们怎么知道向左向右能延伸多远？观察下面几种情况：

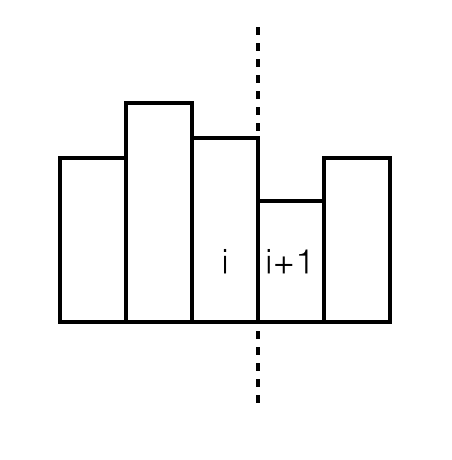
情况1，第i个矩形比右边相邻的第i+1个矩形高，如下图所示。意味着，以height[i]为高的矩形的右边界就是第i个矩形，因为右边界不能更右了（废话），也不会在左边（向左只会让矩形面积减小）。所以在这种情况下，我们可以立即确定以第i个矩形的高度height[i]为高度的最大矩形面积的右边界。

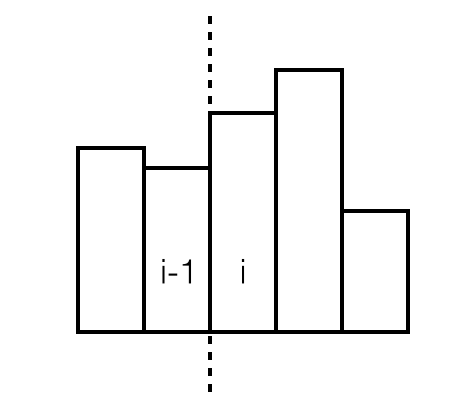
情况2，第i个矩形比左边相邻的第i-1个矩形高，如下图所示。意味着，以height[i]为高的矩形的左边界就是第i个矩形，因为左边界不能更左了（废话），也不会出现在右边（因为向右只会另矩形面积减小）。所以在这种情况下，我们立即就可以确定以第i个矩形的高度height[i]为高度的最大举行面积的左边界。

现在，我们依次遍历各个矩形条，遍历过的矩形条压入栈中保存，则不难发现下面的现象：

如果当前矩形条的高度高于栈顶的矩形条的高度，对应上面的情况2，我们可以立即得出，当前矩形一定是以它为高的矩形的左边界。那么现在我们还不能确定其右边界，所以除了入栈什么都不用做，如下图所示：

如果当前矩形条的高度小于或等于栈顶矩形条的高度，对应上面的情况1，我们可以立即得出：栈顶的矩形一定是以它为高的矩形的右边界所以，我们可以立刻得到以栈顶的矩形条高度为高度的最大矩形的面积（下图中带颜色的两个矩形）！既然我们算出了前一个条最大矩形的面积，那么也就没必要再留着它了。所以，可以放心把它删掉，或者说合并。

 

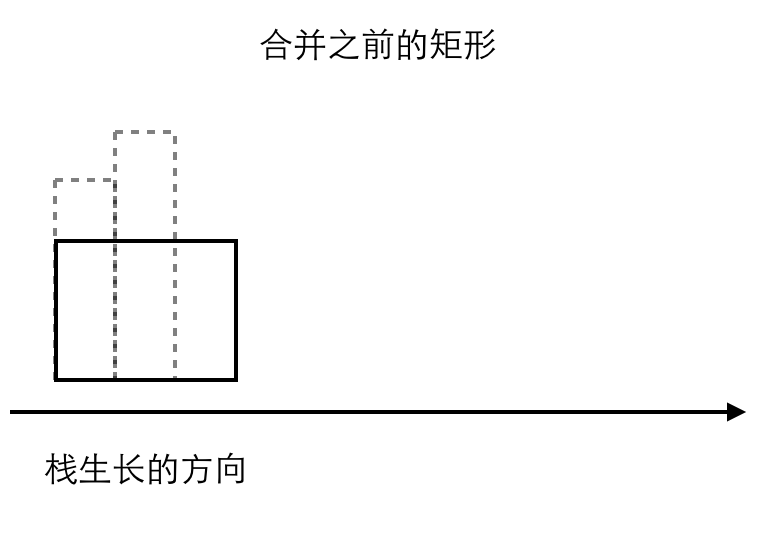
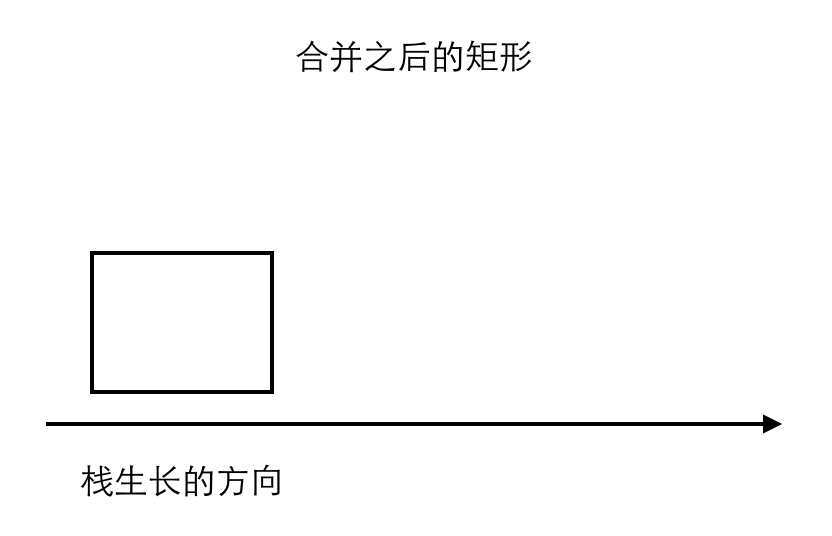
按照上述操作遍历完所有矩形条之后，栈中的矩形一定是下面这个样子。（栈里面所有的条肯定是按照高度依次递增的）

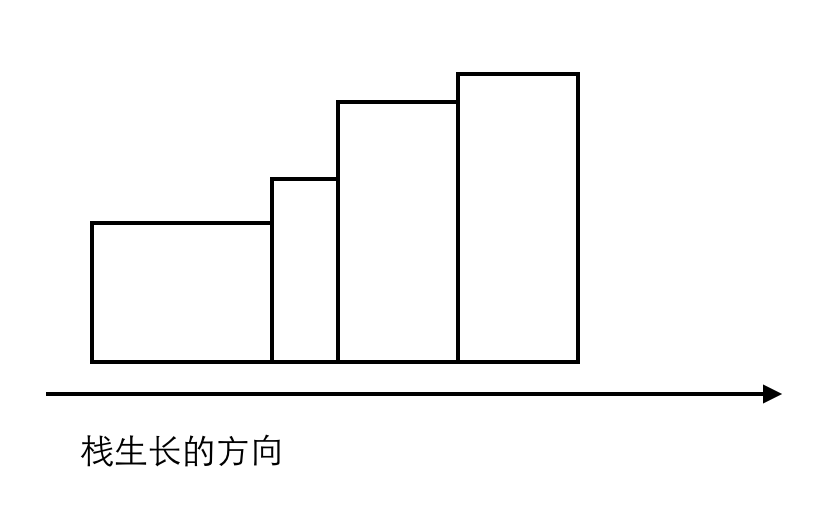
此时，对于任何一个矩形条，我们可以确定，它的右边界一定是整个栈里所保留的条形图的最右边界，而它的左边界一定是它这个条自己的左边界，所以，剩余的矩形条也可以立即算出其对应的最大矩形的面积。

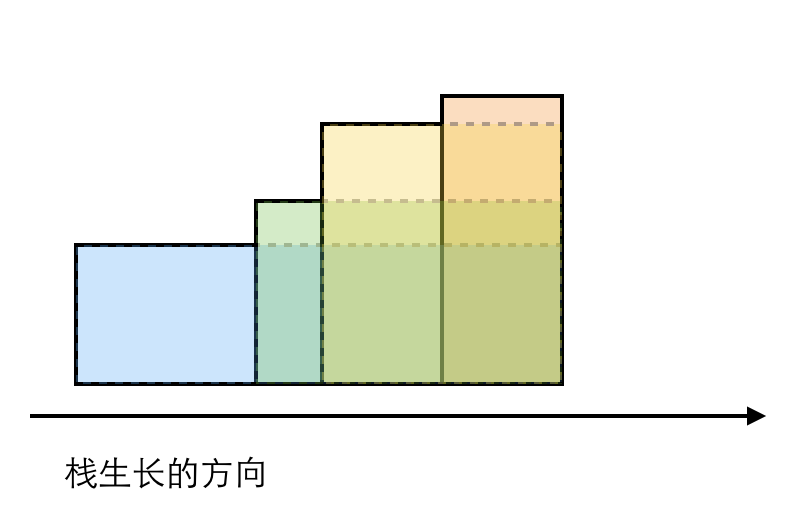
其实，只需要在所有的矩形条最后添加一个高度为0的虚拟矩形条，可以省略上面的两小步。这个虚拟矩形条起收割作用。（见代码第2行）

显然时间复杂度是O(n)。

 

具体代码实现有两个技巧：

1. 我们只需要在辅助栈保存矩形的右边界坐标即可，不需要保存高度，因为可以通过右边界坐标得到（height[i] ），也不需要保存左边界坐标，因为上一个矩形的右边界坐标+1就是当前矩形的左边界。

2. 在直方图最后添加一个高度为0的虚拟矩形条，这样保证一次遍历之后栈里面的矩形都被正确处理过了，否则需要再重复一遍。

代码：

    int largestRectangleArea(vector<int> &height) {
        height.push_back(0); // 添加虚拟矩形条
        stack<int> st;
        int n = height.size();
        int maxArea = 0;
        int h, w;

        for (int i = 0; i < n; i++) {
            if (st.empty() || height[st.top()] < height[i])
                st.push(i);
            else {
                while (!st.empty() && height[i] <= height[st.top()]) {
                    h = height[st.top()];
                    st.pop();
                    w = st.empty() ? i : i - (st.top() + 1);
                    maxArea = max(maxArea, h * w);
                }
                st.push(i);
            }
        }

        return maxArea;
    }