定义
倍增就是 “成倍增加” 的意思,比如1倍增后变成了2,2 倍增后就变成了4,4 变成8,以此类推...
分类
倍增算法总体上可以分为三种类型:
1.快速幂
2.LCA
3.RMQ(ST表)
快速幂
快速幂有什么用呢?
其实用它解决的问题非常简单;
例:2的0次幂是多少:很简单
2的10次幂是多少:可以?
2的18次幂是多少:没问题?
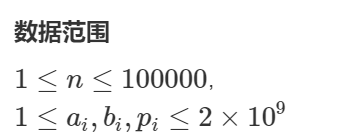
……………………
这种问题呢,就可以用到快速幂,倍增思想.
倍增思想:按倍增加.
例题感受
给定 nn 组 ai,bi,piai,bi,pi,对于每组数据,求出 abiimodpiaibimodpi 的值。
输入格式
第一行包含整数 nn。
接下来 nn 行,每行包含三个整数 ai,bi,piai,bi,pi。
输出格式
对于每组数据,输出一个结果,表示 abiimodpiaibimodpi 的值。
每个结果占一行。
数据范围
1≤n≤1000001≤n≤100000,
1≤ai,bi,pi≤2×1091≤ai,bi,pi≤2×109
输入样例:
2
3 2 5
4 3 9
输出样例:
4
1代码:
#include<bits/stdc++.h> #define ll long long using namespace std; int qmi(int a,int k,int q) { ll res=1; while(k) { if(k&1) res=(ll)res*a%q; //k的二进制末尾是1,说明其用2的次方表示k,从而可以表示出a的k次方 k>>=1; //k右移(相当于除以2),就是把二进制代表的数末尾删掉 a=(ll)a*a%q; //这是处理出a的各种次方,就是反复乘以,当上面if条件成立时,就用处理过的a } return res; } int main() { int n; scanf("%d",&n); while(n--) { int a,k,q; scanf("%d%d%d",&a,&k,&q); printf("%d\n",qmi(a,k,q)); } return 0; }
LCA
这个没啥好讲的,上模板了
#include<bits/stdc++.h>//标准头文件 using namespace std; const int MAXN = 1000010; inline void read(int &n) { char c = getchar(); bool flag = 0; n = 0; while (c < '0' || c > '9') c == '-' ? flag = 1, c = getchar() : c = getchar(); while (c >= '0' && c <= '9') n = n * 10 + c - 48, c = getchar(); flag == 1 ? n = -n : n = n; } struct node { int v, nxt; } edge[MAXN]; int head[MAXN]; int num = 1; inline void add_edge(int x, int y) { edge[num].v = y; edge[num].nxt = head[x]; head[x] = num++; } int f[MAXN][21]; int deep[MAXN]; int n, m, root; void dfs(int now) { for (int i = head[now]; i != -1; i = edge[i].nxt) if (!deep[edge[i].v]) deep[edge[i].v] = deep[now] + 1, f[edge[i].v][0] = now, dfs(edge[i].v); } void PRE() { for (int i = 1; i <= 19; i++) for (int j = 1; j <= n; j++) f[j][i] = f[f[j][i - 1]][i - 1]; } int LCA(int x, int y) { if (deep[x] < deep[y]) swap(x, y); for (int i = 19; i >= 0; i--) if (deep[f[x][i]] >= deep[y]) x = f[x][i]; if (x == y) return x; for (int i = 19; i >= 0; i--) if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i]; return f[x][0]; } int main() { memset(head, -1, sizeof(head)); read(n); read(m); read(root); for (int i = 1; i <= n - 1; i++) { int x, y; read(x); read(y); add_edge(x, y); add_edge(y, x); } deep[root] = 1; dfs(root); PRE(); for (int i = 1; i <= m; i++) { int x, y; read(x); read(y); printf("%d\n", LCA(x, y)); } return 0; }
ST表
例题:
P3865 【模板】ST 表
题目背景
这是一道 ST 表经典题——静态区间最大值
请注意最大数据时限只有 0.8s,数据强度不低,请务必保证你的每次查询复杂度为 O(1)O(1)。若使用更高时间复杂度算法不保证能通过。
如果您认为您的代码时间复杂度正确但是 TLE,可以尝试使用快速读入:
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
函数返回值为读入的第一个整数。
快速读入作用仅为加快读入,并非强制使用。
题目描述
给定一个长度为 NN 的数列,和 MM 次询问,求出每一次询问的区间内数字的最大值。
输入格式
第一行包含两个整数 N,MN,M,分别表示数列的长度和询问的个数。
第二行包含 NN 个整数(记为 a_iai),依次表示数列的第 ii 项。
接下来 MM 行,每行包含两个整数 l_i,r_ili,ri,表示查询的区间为 [l_i,r_i][li,ri]。
输出格式
输出包含 MM 行,每行一个整数,依次表示每一次询问的结果。
输入输出样例
8 8 9 3 1 7 5 6 0 8 1 6 1 5 2 7 2 6 1 8 4 8 3 7 1 8
9 9 7 7 9 8 7 9
通过题目,我们就可以看出这是一道水题,水水的黄题,
哪里有不要的道理?
代码
#include<bits/stdc++.h> using namespace std; inline int read() { int num=0,w=1; char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();} while(ch>='0'&&ch<='9') {num=(num<<1)+(num<<3)+ch-'0';ch=getchar();} return num*w; } int n,m,l,r,k; int a[100001]; int f[100001][30]; int Log[100001]; void st(){ Log[0]=-1; for(register int i=1;i<=n;i++) Log[i]=Log[i>>1]+1; for(register int i=1;i<=n;i++) f[i][0]=a[i]; for(register int j=1;j<=Log[n];j++) for(register int i=1;i+(1<<j)-1<=n;i++) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); return; } int main(){ n=read(),m=read(); for(register int i=1;i<=n;i++) a[i]=read(); st(); while(m--){ l=read(),r=read(); k=Log[r-l+1]; printf("%d\n",max(f[l][k],f[r-(1<<k)+1][k])); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号