搜索算法

深度优先搜索（爆搜）

引入：

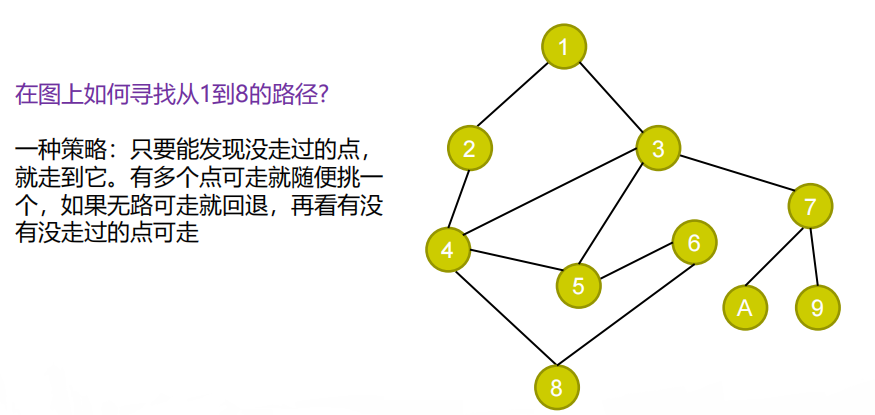
定义：

　　深度优先搜索(Depth-First-Search），简称DFS；

从起点出发，走过的点要做标记，发现有没走过的点，就随意挑一个往前走，走不

了就回退，此种路径搜索策略就称为“深度优先搜索”，简称“深搜”。

其实称为“远度优先搜索”更容易理解些。因为这种策略能往前走一步就往前走一

步，总是试图走得更远。所谓远近(或深度），就是以距离起点的步数来衡量的。

伪代码：

bool Dfs(V) {
    if( V 为终点）
            return true;
            if( V 为旧点)
                return false;
                将V标记为旧点;
        对和V相邻的每个节点U {
        if( Dfs(U) == true)
                return true;
        }
    return false;
}
int main() {
    将所有点都标记为新点;
    起点 = 1
           终点 = 8
                  cout << Dfs(起点）;
}

这里的搜索都是用做图，而图的储存我们用邻接矩阵和邻接表来存储.

例题：

P2404 自然数的拆分问题

题目描述

任何一个大于

输入格式

输入：待拆分的自然数

输出格式

输出：若干数的加法式子。

输入输出样例

输入 #1

输出 #1

1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4

代码：

#include<iostream>
using namespace std;
int a[100001]={1},n;
int search(int,int);
int print(int);
int search(int s,int t){
    for(int i=a[t-1];i<=s;i++){
        if(i<n){
            a[t]=i;
            s=s-i;
            if(s==0) print(t);
            else search(s,t+1);
            s+=i;
        }
    }
}
int print(int t){
    for(int i=1;i<t;i++){
        cout<<a[i]<<"+";
    }
    cout<<a[t]<<endl;
}
int main(){
    cin>>n;
    search(n,1);
    return 0;
}

P1219 [USACO1.5]八皇后 Checker Challenge

题目描述

一个如下的 $\times 66×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。$

上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 52 4 6 1 3 5 来描述，第 ii 个数字表示在第 ii 行的相应位置有一个棋子，如下：$

行号 $1\ 2\ 3\ 4\ 5\ 61 2 3 4 5 6$

列号 $2\ 4\ 6\ 1\ 3\ 52 4 6 1 3 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前

输入格式

一行一个正整数 $\times nn×n 大小的。$

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例

输入 #1

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

代码：

#include<bits/stdc++.h>
using namespace std;
int n,cnt=0;
bool lie[25];//列 
bool u[40];
bool v[40];
int a[40];
void pr(){
    if(cnt<3){
        for(int i=1;i<=n;i++){
            cout<<a[i]<<" ";
        }
        cout<<endl;
    }
}
void dfs(int x){
    if(x>n){
        pr();
        cnt++;
        return ;
    }
    for(int i=1;i<=n;i++){
        if(!lie[i]&&!u[x-i+n]&&!v[x+i]){
            lie[i]=1;
            u[x-i+n]=1;
            v[x+i]=1;
            a[x]=i;
            dfs(x+1);
            lie[i]=0;
            u[x-i+n]=0;
            v[x+i]=0;
        } 
    }
}
int main(){
    scanf("%d",&n);
    dfs(1);
    cout<<cnt; 
    return 0;
}

P1205 [USACO1.2] 方块转换 Transformations

题目描述

一块 $\times nn×n 正方形的黑白瓦片的图案要被转换成新的正方形图案。写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式：$

转 $90\degree90°：图案按顺时针转 90\degree90°。$
转 $180\degree180°：图案按顺时针转 180\degree180°。$
转 $270\degree270°：图案按顺时针转 270\degree270°。$
反射：图案在水平方向翻转（以中央铅垂线为中心形成原图案的镜像）。
组合：图案在水平方向翻转，然后再按照 $\sim 31∼3 之间的一种再次转换。$
不改变：原图案不改变。
无效转换：无法用以上方法得到新图案。

如果有多种可用的转换方法，请选择序号最小的那个。

只使用上述

输入格式

第一行一个正整数

然后

接下来

输出格式

单独的一行包括 $\sim 71∼7 之间的一个数字（在上文已描述）表明需要将转换前的正方形变为转换后的正方形的转换方法。$

输入输出样例

输入 #1

3
@-@
---
@@-
@-@
@--
--@

输出 #1

代码：

#include<bits/stdc++.h>
using namespace std;
int n;
char a[15][15];
char b[15][15];
char c[15][15];
char d[15][15];
bool work1() {
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++)
            b[j][n-i+1]=a[i][j];
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(b[i][j]!=c[i][j])
                return 0;
    return 1;
}
bool work2() {
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++)
            b[n-i+1][n-j+1]=a[i][j];
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(b[i][j]!=c[i][j])
                return 0;
    return 1;
}
bool work3() {
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++)
            b[n-j+1][i]=a[i][j];
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(b[i][j]!=c[i][j])
                return 0;
    return 1;
}
bool work4() {
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++)
            b[i][n-j+1]=a[i][j];
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(b[i][j]!=c[i][j])
                return 0;
    return 1;
}
bool work5() {
    work4();
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            a[i][j]=b[i][j];
    if(work1())
        return 1;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            a[i][j]=b[i][j];
    if(work2())
        return 1;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            a[i][j]=b[i][j];
    if(work3())
        return 1;
    return 0;
}
bool work6() {
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(b[i][j]!=c[i][j])
                return 0;
    return 1;
}
void work() {
    if(work1()) {
        cout<<1;
        return ;
    }
    if(work2()) {
        cout<<2;
        return ;
    }
    if(work3()) {
        cout<<3;
        return ;
    }
    if(work4()) {
        cout<<4;
        return ;
    }
    if(work5()) {
        cout<<5;
        return ;
    }
    if(work6()) {
        cout<<6;
        return ;
    }
    cout<<7;
}
int main() {
    cin>>n;
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++) {
            cin>>a[i][j];
            d[i][j]=a[i][j];
        }
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            cin>>c[i][j];
    work();
    return 0;
}

P1706 全排列问题

题目描述

按照字典序输出自然数

输入格式

一个整数

输出格式

由 $\sim n1∼n 组成的所有不重复的数字序列，每行一个序列。$

每个数字保留

输入输出样例

输入 #1

输出 #1

    1    2    3
    1    3    2
    2    1    3
    2    3    1
    3    1    2
    3    2    1
代码：

#include<bits/stdc++.h>
using namespace std;
int n;
bool vis[100];
int a[100];
void pr(){
    for(int i=1;i<=n;i++){
        cout<<setw(5)<<a[i];
    }
    cout<<endl;
}
void dfs(int x){
    if(x>n){
        pr();
    }
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            a[x]=i;
            vis[i]=1;
            dfs(x+1);
            vis[i]=0;
        }
    }
}
int main(){
    scanf("%d",&n);
    dfs(1);
    return 0;
}

广度优先搜索

定义：

　　广度优先搜索（Breadth First Search，BFS）广度优先搜索是一种分层的查找过程，每向前一层可能会访问一批顶点，

不像深度优先搜索有回溯的过程

例题：

走迷宫

给定一个

最初，有一个人位于左上角

请问，该人从左上角移动至右下角

数据保证

输入格式

第一行包含两个整数

接下来

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

输入样例：

输出样例：

code

#include<bits/stdc++.h>
using namespace std;
int bfs(string state) {
    queue<string> q;
    unordered_map<string, int> d;
    q.push(state);
    d[state] = 0;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    string end = "12345678x";
    while (q.size()) {
        auto t = q.front();
        q.pop();
        if (t == end) return d[t];
        int distance = d[t];
        int k = t.find('x');
        int x = k / 3, y = k % 3;
        for (int i = 0; i < 4; i ++ ) {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3) {
                swap(t[a * 3 + b], t[k]);
                if (!d.count(t)) {
                    d[t] = distance + 1;
                    q.push(t);
                }
                swap(t[a * 3 + b], t[k]);
            }
        }
    }
    return -1;
}
int main() {
    char s[2];
    string state;
    for (int i = 0; i < 9; i ++ ) {
        cin >> s;
        state += *s;
    }
    cout << bfs(state) << endl;
    return 0;
}

搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索搜索

posted on 2022-07-29 22:08 博然后深阅读(147) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

搜索算法

深度优先搜索（爆搜）

引入：

定义：

伪代码：

例题：

P2404 自然数的拆分问题

题目描述

输入格式

输出格式

输入输出样例

P1219 [USACO1.5]八皇后 Checker Challenge

题目描述

输入格式

输出格式

输入输出样例

P1205 [USACO1.2] 方块转换 Transformations

题目描述

输入格式

输出格式

输入输出样例

P1706 全排列问题

题目描述

输入格式

输出格式

输入输出样例

广度优先搜索

定义：

例题：

走迷宫

输入格式

输出格式

数据范围

输入样例：

输出样例：