2022.7.29学习笔记

主要内容：

1.AC自动机.
2.线性DP.
3.区间DP.
4.背包DP.
5.树形DP.
6.数位DP.

AC自动机

神犇：~~AC自动机，听这名字，就能推测是能自动 AC 的算法.~~

虽然不能自动帮我们AC所有算法题，但确实能让我们AC一些题目.

定义：

AC自动机主要用于解决多模式串的匹配问题，是字典树(trie树)的变种，一种伪树形

结构(主体是树形的，但是由于加入了失败指针，使得它变成了一个有向图)；

来看一下AC自动机与同类的区别.

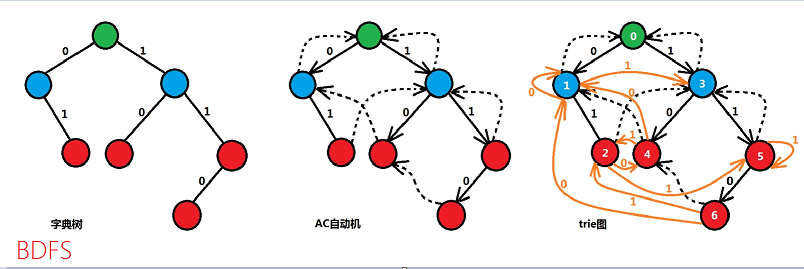
上例题：

1282. 搜索关键词

给定

请问，其中有多少个单词在文章中出现了。

注意：每个单词不论在文章中出现多少次，仅累计

输入格式

第一行包含整数

对于每组数据，第一行一个整数

输出格式

对于每组数据，输出一个占一行的整数，表示有多少个单词在文章中出现。

数据范围

输入样例：

1
5
she
he
say
shr
her
yasherhs

输出样例：

3

直接上AC自动机自动写的code：

#include<bits/stdc++.h>
using namespace std;
const int N = 10010, S = 55, M = 1000010;
int n;
int tr[N * S][26], cnt[N * S], idx;
char str[M];
int q[N * S], ne[N * S];
void insert() {
    int p = 0;
    for (int i = 0; str[i]; i ++ ) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++ idx;
        p = tr[p][t];
    }
    cnt[p] ++ ;
}
void build() {
    int hh = 0, tt = -1;
    for (int i = 0; i < 26; i ++ )
        if (tr[0][i])
            q[ ++ tt] = tr[0][i];
    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = 0; i < 26; i ++ ) {
            int p = tr[t][i];
            if (!p) tr[t][i] = tr[ne[t]][i];
            else {
                ne[p] = tr[ne[t]][i];
                q[ ++ tt] = p;
            }
        }
    }
}
int main() {
    int T;
    scanf("%d", &T);
    while (T -- ) {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ ) {
            scanf("%s", str);
            insert();
        }
        build();
        scanf("%s", str);
        int res = 0;
        for (int i = 0, j = 0; str[i]; i ++ ) {
            int t = str[i] - 'a';
            j = tr[j][t];
            int p = j;
            while (p) {
                res += cnt[p];
                cnt[p] = 0;
                p = ne[p];
            }
        }
        printf("%d\n", res);
    }
    return 0;
}

了解更多DP请点这（以前写过的动态规划合集）

https://www.cnblogs.com/boranhoushen/p/16479066.html

线性DP

经典例题：

1259：【例9.3】求最长不下降序列

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

设有由 $n (1 \leq n \leq 200)$

例如13，7，9，16，38，24，37，18，44，19，21，22，63，15。例中13，16，18，19，21，22，63就是一个长度为 $7$

【输入】

第一行为 $n$

【输出】

第一行为输出最大个数 $m a x$

第二行为 $m a x$

【输入样例】

14
13 7 9 16 38 24 37 18 44 19 21 22 63 15

【输出样例】

max=8
7 9 16 18 19 21 22 63

代码：

#include<iostream>
using namespace std;
int n,a[1001],f[1001],p[1001],ans;
void dfs(int i) {
    if(p[i]>0) dfs(p[i]);
    cout<<a[i]<<" ";
}
int main() {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    f[1]=1;
    p[1]=0;
    for(int i=2; i<=n; i++) {
        f[i]=0;
        for(int j=1; j<=i; j++)
            if(a[j]<=a[i]&&f[j]>f[i]) {
                f[i]=f[j];
                p[i]=j;
            }
        f[i]++;
    }
    int ans=0,k=0;
    for(int i=1; i<=n; i++)
        if(f[i]>ans) ans=f[k=i];
    cout<<"max="<<ans<<endl;
    dfs(k);
    return 0;
}

区间DP

经典例题：

1261：【例9.5】城市交通路网

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 8917 通过数: 6364

【题目描述】

下图表示城市之间的交通路网，线段上的数字表示费用，单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。

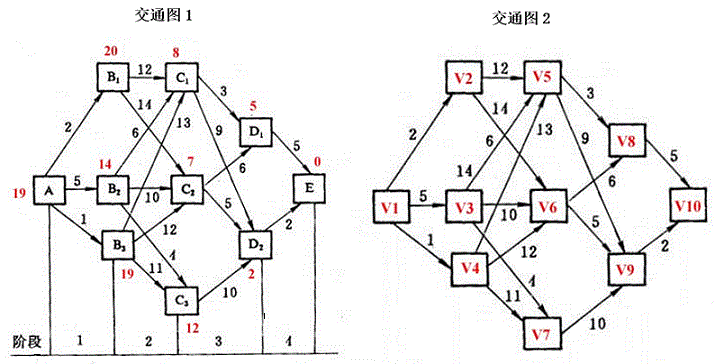
如图：求v1到v10的最短路径长度及最短路径。

【输入】

第一行为城市的数量N;

后面是N*N的表示两个城市间费用组成的矩阵。

【输出】

A->E的最省费用。

【输入样例】

10
0  2  5  1  0  0  0  0  0  0
0  0  0  0 12 14  0  0  0  0
0  0  0  0  6 10  4  0  0  0
0  0  0  0 13 12 11  0  0  0
0  0  0  0  0  0  0  3  9  0
0  0  0  0  0  0  0  6  5  0
0  0  0  0  0  0  0  0 10  0
0  0  0  0  0  0  0  0  0  5
0  0  0  0  0  0  0  0  0  2
0  0  0  0  0  0  0  0  0  0

【输出样例】

minlong=19
1 3 5 8 10

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=101;
const int inf=0x7f7f7f7f;
int n;
int map[maxn][maxn];
bool vis[maxn];
int dis[maxn];
int pre[maxn];
int f=1;
int read() {
    int x=0,f=1;
    char c=getchar();
    while(!isdigit(c)) {
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while(isdigit(c)) {
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}
void print(int x) {
    if(x==0)return;
    else {
        print(pre[x]);
        printf("%d ",x+1);
    }
}
void work() {
    n=read();
    memset(dis,inf,sizeof(dis));
    for (int i=0; i<n; i++)
        for (int j=0; j<n; j++) {
            map[i][j]=read();
            if(map[i][j]==0)
                map[i][j]=inf;
            else if(i==0)
                dis[j]=map[i][j];
        }
    dis[0]=0;
    for(int i=0; i<n; i++) {
        int  minn=inf,x=0;
        for (int j=0; j<n; j++) {
            if(!vis[j]&&minn>dis[j])
                minn=dis[j],x=j;
        }
        vis[x]=1;
        for (int j=0; j<n; j++)
            if(map[x][j]+dis[x]<dis[j]) {
                pre[j]=x;
                dis[j]=map[x][j]+dis[x];
            }
    }
    printf("minlong=%d\n",dis[n-1]);
    printf("1 ");
    print(n-1);
}
int main() {
    work();
    return 0;
}

背包DP

01背包：

code

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i )
        for (int j = m; j >= v[i]; j – )
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

完全背包：

code

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

多重背包：

code

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ )
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    cout << f[n][m] << endl;
    return 0;
}

分组背包：

code

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }
    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m] << endl;
    return 0;
}

树形DP

没有上司的舞会

Ural 大学有

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式

第一行一个整数

接下来

输出格式

输出最大的快乐指数。

数据范围

输入样例：

输出样例：

代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 6010;
int n;
int h[N], e[N], ne[N], idx;
int happy[N];
int f[N][2];
bool has_fa[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u) {
    f[u][1] = happy[u];
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        dfs(j);
        f[u][1] += f[j][0];
        f[u][0] += max(f[j][0], f[j][1]);
    }
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ ) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(b, a);
        has_fa[a] = true;
    }
    int root = 1;
    while (has_fa[root]) root ++ ;
    dfs(root);
    printf("%d\n", max(f[root][0], f[root][1]));
    return 0;
}

数位DP

338. 计数问题

给定两个整数

例如，

1024 1025 1026 1027 1028 1029 1030 1031 1032

其中 0 出现

输入格式

输入包含多组测试数据。

每组测试数据占一行，包含两个整数

当读入一行为 0 0 时，表示输入终止，且该行不作处理。

输出格式

每组数据输出一个结果，每个结果占一行。

每个结果包含十个用空格隔开的数字，第一个数字表示 0 出现的次数，第二个数字表示 1 出现的次数，以此类推。

数据范围

输入样例：

输出样例：

1 2 1 1 1 1 1 1 1 1
85 185 185 185 190 96 96 96 95 93
40 40 40 93 136 82 40 40 40 40
115 666 215 215 214 205 205 154 105 106
16 113 19 20 114 20 20 19 19 16
107 105 100 101 101 197 200 200 200 200
413 1133 503 503 503 502 502 417 402 412
196 512 186 104 87 93 97 97 142 196
398 1375 398 398 405 499 499 495 488 471
294 1256 296 296 296 296 287 286 286 247

代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int get(vector<int> num, int l, int r) {
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}
int power10(int x) {
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}
int count(int n, int x) {
    if (!n) return 0;
    vector<int> num;
    while (n) {
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();
    int res = 0;
    for (int i = n - 1 - !x; i >= 0; i -- ) {
        if (i < n - 1) {
            res += get(num, n - 1, i + 1) * power10(i);
            if (!x) res -= power10(i);
        }
        if (num[i] == x) res += get(num, i - 1, 0) + 1;
        else if (num[i] > x) res += power10(i);
    }
    return res;
}
int main() {
    int a, b;
    while (cin >> a >> b , a) {
        if (a > b) swap(a, b);
        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }
    return 0;
}

（接到一些同学提的意见，说不要水博客了，蒟蒻本蒟也不是水博客，

是真的没学会，但以后我会尽量将内容多写一些）

posted on 2022-07-29 21:09 博然后深阅读(70) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

2022.7.29学习笔记

主要内容：

AC自动机

定义：

上例题：

1282. 搜索关键词

输入格式

输出格式

数据范围

输入样例：

输出样例：

线性DP

经典例题：

1259：【例9.3】求最长不下降序列

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

区间DP

经典例题：

1261：【例9.5】城市交通路网

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

背包DP

01背包：

完全背包：

多重背包：

分组背包：

树形DP

没有上司的舞会

输入格式

输出格式

数据范围

输入样例：

输出样例：

数位DP

338. 计数问题

输入格式

输出格式

数据范围

输入样例：

输出样例：