2022.7.25学习笔记

主要内容：

1.单调栈

2.单调队列

3.前缀和

4.差分

5.STL

6.贪心

7.分治

8.二分

单调栈

定义：

1.单调栈，顾名思义，即保证内部元素单调（从大到小或者从小到

大）的栈。我们只要在插入新元素的时候，将栈顶所有在插

入新元素后不满足单调的元素依次弹出，再插入新元素即可。

2.单调栈中的元素满足单调性。

3.通常用在DP的优化中。

特点及分类：

1.栈内元素单调按照递增（递减）顺序排列的栈。

2.分为单调递增栈和单调递减栈，通过单调栈可以访问到下一个比它大（小）的元素，也

就是从数组中找到左右两边比它大的数或者比它小的数，而且时间复杂度是O(n)。

3.单调递增栈：从栈底到栈顶是递增的，栈中保留的都是比当前入栈元素小的值。（不唯一）

4.单调递减栈：从栈底到栈顶是递减的，栈中保留的都是比当前入栈元素大的值。（不唯一）

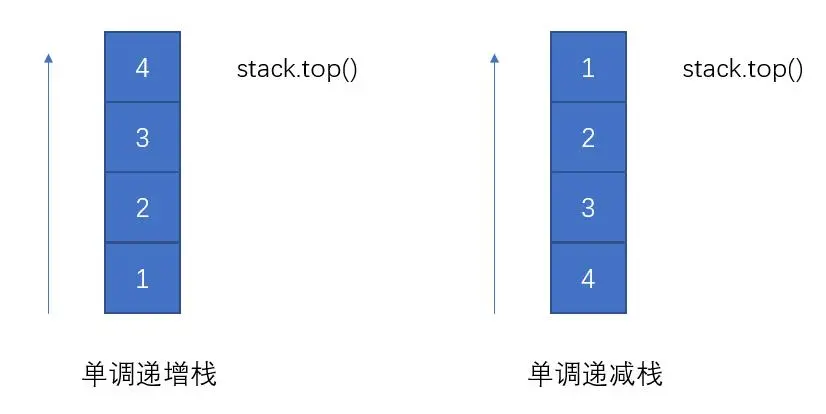
例题：

P5788 【模板】单调栈（https://www.luogu.com.cn/problem/P5788）

题目描述

给出项数为 $a_{1 \dots n}a1…n。$

定义函数 $a_iai 的元素的下标，即 f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}f(i)=mini<j≤n,aj>ai{j}。若不存在，则 f(i)=0f(i)=0。$

试求出 $f(1\dots n)f(1…n)。$

输入格式

第一行一个正整数

第二行 $a_{1\dots n}a1…n。$

输出格式

一行 $f(1\dots n)f(1…n) 的值。$

输入输出样例

输入 #1

5
1 4 2 3 5

输出 #1

2 5 4 5 0

说明/提示

【数据规模与约定】

对于 $30\%30% 的数据，n\leq 100n≤100；$

对于 $60\%60% 的数据，n\leq 5 \times 10^3n≤5×103 ；$

对于 $100\%100% 的数据，1 \le n\leq 3\times 10^61≤n≤3×106，1\leq a_i\leq 10^91≤ai≤109。$

#include<bits/stdc++.h>
using namespace std;
const int N=10e6+5;
long long n,a[N],q[N],f[N];
long long top=0;
int main() {
    scanf("%d",&n);
    for(int i=1; i<=n; i++) scanf("%d",&a[i]);
    for(int i=n; i>=1; i--) {
        while (a[i]>=a[q[top]]&&top>0) top--;
        f[i]=q[top];
        q[++top]=i;
    }
    for(int i=1; i<=n; i++) printf("%d ",f[i]);
    return 0;
}

注意数据范围，不然……

单调队列

定义：

1.单调队列，顾名思义，即保证内部元素单调（从大到小或者从小到

大）的队列。我们只要在插入新元素的时候，将队尾所有在插

入新元素后不满足单调的元素依次弹出，再插入新元素即可。

2.单调队列中的元素满足单调性。

3.单调队列只能解决一个叫滑动窗口的问题。

例题：

P1886 滑动窗口 /【模板】单调队列（https://www.luogu.com.cn/problem/P1886）

题目描述

有一个长为

例如：

The array is

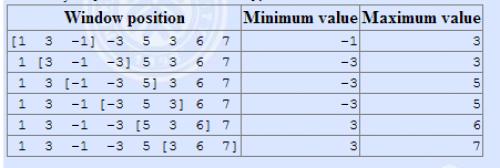
输入格式

输入一共有两行，第一行有两个正整数

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

输入输出样例

输入 #1

8 3
1 3 -1 -3 5 3 6 7

输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明/提示

【数据范围】
对于 $50\%50% 的数据，1 \le n \le 10^51≤n≤105；对于 100\%100% 的数据，1\le k \le n \le 10^61≤k≤n≤106，a_i \in [-2^{31},2^{31})ai∈[−231,231)。$

#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,k,a[N+5],s[N+5];
int head=1,tail=0;
int main() {
    scanf("%d%d",&n,&k);
    for(int i=1; i<=n; i++) {
        scanf("%d",&a[i]);
    }
    for(int i=1; i<=n; i++) {
        while(head<=tail&&s[head]+k<=i) head++;
        while(head<=tail&&a[i]<a[s[tail]]) tail--;
        s[++tail]=i;
        if(i>=k) printf("%d ",a[s[head]]);
    }
    cout<<endl;
    memset(s,0,sizeof(s));
    for(int i=1; i<=n; i++) {
        while(head<=tail&&s[head]+k<=i) head++;
        while(head<=tail&&a[i]>a[s[tail]]) tail--;
        s[++tail]=i;
        if(i>=k) printf("%d ",a[s[head]]);
    }
    return 0;
}

这里没什么可讲的，重点就是四个while循环

前缀和

定义：

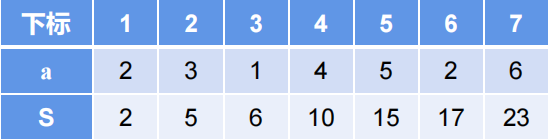
1.对于一维数组a，前缀和S[i]表示的就是a[1]+a[2]+…+a[i].（a[i]=a[i-1]+a[i]）

一维前缀和模板：

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m;
int a[N],s[N];
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++) scanf("%d", &a[i]);
    for(int i=1; i<=n; i++) s[i]=s[i-1]+a[i];//前缀和的初始化
    while(m--) {
        int l,r;
        cin>>l>>r;
        printf("%d\n",s[r]-s[l-1]);//区间和的计算
    }
    return 0;
}

2.二维前缀和S[i][j]=S[i-1,j]+S[i,j-1]-S[i-1,j-1]+a[i,j].

二维前缀和模板：

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],s[N][N];
int main() {
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            scanf("%d",&a[i][j]);//正常输入输出 
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)//前缀和的初始化
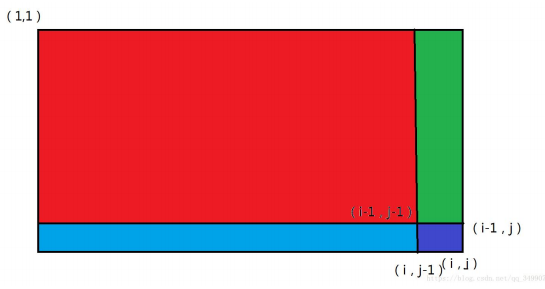
            s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1];//提前计算 
    while(q--) {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);//将数据带入求区间和 
    }
    return 0;
}

差分

1.一维差分：b[1]=a[1]; b[2]=a[2]-a[1]; b[3]=a[3]-a[2]; .......

一维差分模板：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main() {
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++) {
        scanf("%d",&a[i]);
        b[i]=a[i]-a[i-1];//构建差分数组
    }
    int l,r,c;
    while(m--) {
        scanf("%d%d%d",&l,&r,&c);
        b[l]+=c;//表示将序列中[l, r]之间的每个数加上c
        b[r+1]-=c;
    }
    for(int i=1; i<=n; i++) {
        b[i]+=b[i-1];//求前缀和运算
        printf("%d ",b[i]);
    }
    return 0;
}

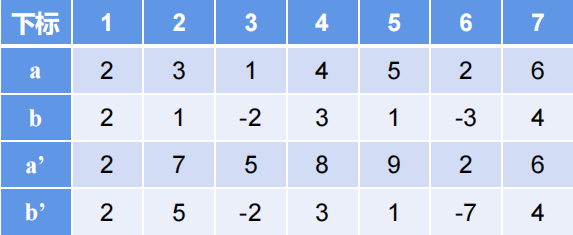
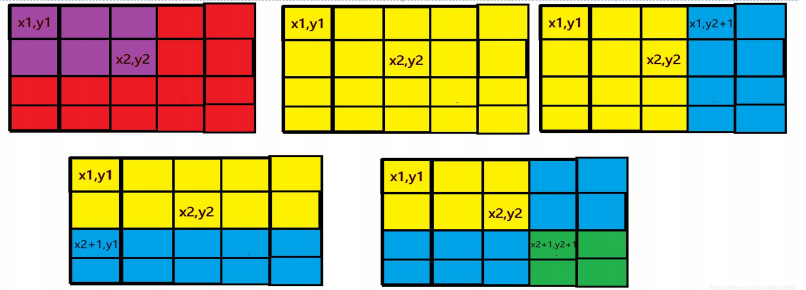
2.二维差分：b[x][y]=a[x][y]+a[x-1][y-1]-a[x-1][y]-a[x][y-1]

二维差分模板：

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c) {
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
int main() {
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            cin>>a[i][j];
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=m; j++) {
            insert(i,j,i,j,a[i][j]);//构建差分数组
        }
    }
    while(q--) {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;//代入数据 
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=m; j++) {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];//方程求 
        }
    }
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=m; j++) {
            printf("%d ",b[i][j]);//输出 
        }
        printf("\n");
    }
    return 0;
}

STL

定义：

　　STL(Standard Template Library,标准模板库)，是惠普实验室开发的一系列软件的统称。现在主要出现在 c++中，但是在引入 c++之前该技术已经存在很长时间了。STL 从广义上分为: 容器(container) 算法(algorithm) 迭代器(iterator),容器和算法之间通过迭代器进行无缝连接。STL 几乎所有的代码都采用了模板类或者模板函数，这相比传统的由函数和类组成的库来说提供了更好的代码重用机会。 STL(Standard Template Library)标准模板库,在我们 c++标准程序库中隶属于 STL 的占到了 80%以上。

优点：

　　有了STL，不必再写大多的标准数据结构和算法，并且可获得非常高的性能。

分类：

　　容器：可容纳各种数据类型的通用数据结构,是类模板
　　迭代器：可用于依次存取容器中元素，类似于指针
　　算法：用来操作容器中的元素的函数模板

容器概述：

1.顺序容器
vector, deque,list
2.关联容器
set, multiset, map, multimap
3.容器适配器
stack, queue, priority_queue

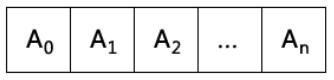
 vector 头文件 <vector>
　　动态数组。元素在内存连续存放。随机存取任何元素都能在常数时间
完成。在尾端增删元素具有较佳的性能(大部分情况下是常数时间）。

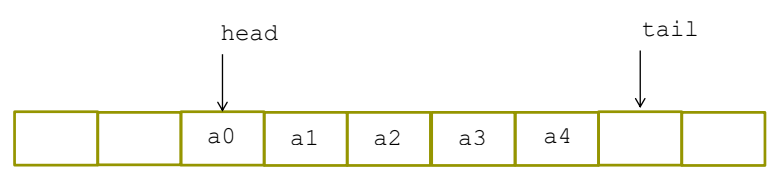
 deque 头文件 <deque>
　　双向队列。元素在内存连续存放。随机存取任何元素都能在常数时间
完成(但次于vector)。在两端增删元素具有较佳的性能(大部分情况下是常
数时间）。

 list 头文件 <list>
　　双向链表。元素在内存不连续存放。在任何位置增删元素都能在常数
时间完成。不支持随机存取。

关联容器:

 set/multiset 头文件 <set>
　　set 即集合。set中不允许相同元素，multiset中允许存在相同的元素。
 map/multimap 头文件 <map>
　　map与set的不同在于map中存放的元素有且仅有两个成员变量，一个
名为first,另一个名为second, map根据first值对元素进行从小到大排序，
并可快速地根据first来检索元素。
　　map同multimap的不同在于是否允许相同first值的元素。

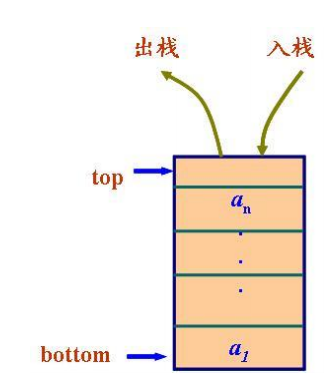
 stack 头文件 <stack>　　

　　栈。是项的有限序列，并满足序列中被删除、检索和修改

的项只能是最近插入序列的项（栈顶的项）。后进先出。

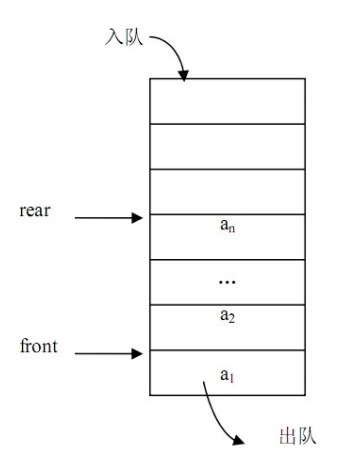
 queue 头文件 <queue>

　　队列。插入只可以在尾部进行，删除、检索和修改只允许从头

部进行。先进先出。

容器适配器:

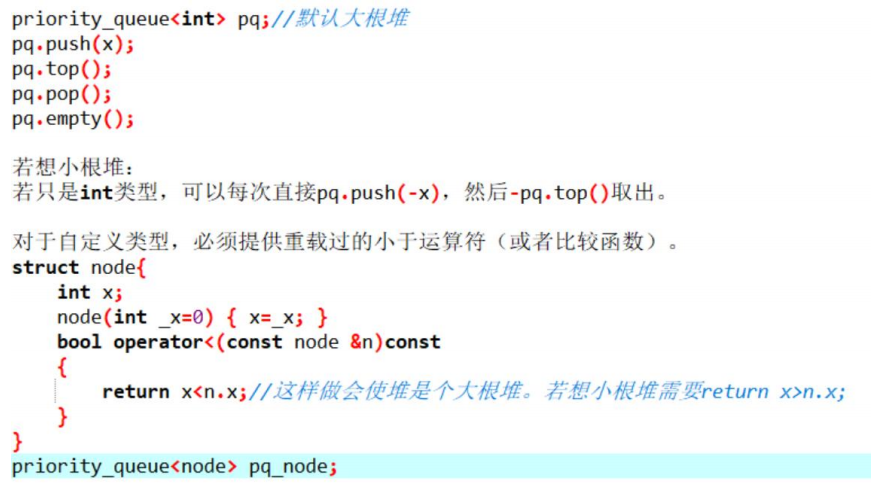
 priority_queue 头文件 <queue>
　　优先级队列。最高优先级元素总是第一个出列

顺序容器和关联容器中都有的成员函数:

　　begin 返回指向容器中第一个元素的迭代器
　　end 返回指向容器中最后一个元素后面的位置的迭代器
　　rbegin 返回指向容器中最后一个元素的迭代器
　　rend 返回指向容器中第一个元素前面的位置的迭代器
　　erase 从容器中删除一个或几个元素
　　clear 从容器中删除所有元素

顺序容器的常用成员函数:

　　front 返回容器中第一个元素的引用
　　back 返回容器中最后一个元素的引用
　　push_back 在容器末尾增加新元素
　　pop_back 删除容器末尾的元素
　　erase 删除迭代器指向的元素(可能会使该迭代器失效），或删
除一个区间，返回被删除元素后面的那个元素的迭代器

迭代器:

定义一个容器类的迭代器的方法可以是：

容器类名::iterator 变量名;或：容器类名::const_iterator 变量名;

访问一个迭代器指向的元素：

* 迭代器变量名

　　迭代器上可以执行 ++ 操作, 以使其指向容器中的下一个元素。
如果迭代器到达了容器中的最后一个元素的后面，此时再使用
它，就会出错，类似于使用NULL或未初始化的指针一样。

迭代器示例:

#include<bits/stdc++.h>
//#include<vector>
using namespace std;
int main() {
    vector<int> v; //一个存放int元素的数组，一开始里面没有元素
    v.push_back(1);
    v.push_back(2);
    v.push_back(3);
    v.push_back(4);
    vector<int>::const_iterator i; //常量迭代器
    for(i=v.begin(); i!=v.end(); i++) cout<<*i << ",";
    cout<<endl;
    vector<int>::reverse_iterator r; //反向迭代器
    for(r=v.rbegin();r!=v.rend();r++) cout<<*r<< ",";
    cout<<endl;
    vector<int>::iterator j; //非常量迭代器
    for(j=v.begin();j!=v.end();j++) *j=100;
    for(i=v.begin();i!=v.end();i++) cout<<*i<<",";
    return 0;
}

algorithm :

●algorithm 库封装了许多函数。

●copy(A + l, A + r, B) 把 A 数组里 [l, r) 开区间拷贝到 B 数组开头。A+l,

A+r 可以换成 vector 的 v.begin(), v.end(), 或者 v.begin()+i。下同

●fill(A + l, A + r, v) 把 A 数组里 [l, r) 都赋值为 v。

●swap(x, y) 交换两个元素。注意由于大部分 stl 容器只包含一个指针，交

换是 O(1) 的。

●reverse(A + l, A + r) 翻转区间 [l, r)。

●sort(A + l, A + r) 排序区间 [l, r)。

●unique(A + l, A + r) 把区间里连续的相同的元素移至末尾，返回剩下的元

素结尾位置。int m = unique(A, A + n) – A;

●nth_element(A + l, A + k, A + r) 把 [l, r) 部分排序，使得 A[k] 这个位置

的元素是正确的，比它小的在左边而比它大的在右边。

●比如 nth_element(A, A + 5, A + 10) 会把第 6 小的（注意从 0 开始）放

到 A[5]，前 5 小以任意顺序放到 A[0...4]，其他以任意顺序放到 A[6...9]。

●lower_bound(A + l, A + r, x) 返回第一个大于等于 x 的位置（要求序列有

序）。取其下标可以 lower_bound(A + l, A + r, x) – A;

●upper_bound 同理，返回第一个大于 x 的位置。

●binary_search(A + l, A + r, x) 二分查找判断 x 是否在这个区间里出现，

只返回true/false。

算法模拟：

#include<bits/stdc++.h>
//#include<list>
//#include<algorithm>
using namespace std;
class A {
    private:
        int n;
    public:
        A(int n_) {//今天天大新知识，活学活用class 
            n = n_;
        }
        friend bool operator<( const A & a1, const A & a2);
        friend bool operator==( const A & a1, const A & a2);
        friend ostream & operator <<( ostream & o, const A & a);
};
bool operator<( const A & a1, const A & a2) {return a1.n < a2.n;}
bool operator==( const A & a1, const A & a2) {return a1.n == a2.n;}
ostream & operator <<( ostream & o, const A & a) {
    o << a.n;
    return o;
}
template <class T>
void PrintList(const list<T> & lst) {
//不推荐的写法，还是用两个迭代器作为参数更好
    int tmp = lst.size();
    if( tmp > 0 ) {
        typename list<T>::const_iterator i;
        i = lst.begin();
        for( i = lst.begin(); i != lst.end(); i ++)
            cout << * i << ",";
    }
}
int main() {
    list<A> lst1,lst2;
    lst1.push_back(1);
    lst1.push_back(3);
    lst1.push_back(2);
    lst1.push_back(4);
    lst1.push_back(2);
    lst2.push_back(10);
    lst2.push_front(20);
    lst2.push_back(30);
    lst2.push_back(30);
    lst2.push_back(30);
    lst2.push_front(40);
    lst2.push_back(40);
    cout << "1) ";
    PrintList( lst1);
    cout << endl;
    cout << "2) ";
    PrintList( lst2);
    cout << endl;
    lst2.sort();
    cout << "3) ";
    PrintList( lst2);
    cout << endl;
    lst2.pop_front();
    cout << "4) ";
    PrintList( lst2);
    cout << endl;
    lst1.remove(2);
    cout << "5) ";
    PrintList( lst1);
    cout << endl;
    lst2.unique(); 
    cout << "6) ";
    PrintList( lst2);
    cout << endl;
    lst1.merge (lst2); 
    cout << "7) ";
    PrintList( lst1);
    cout << endl;
    cout << "8) ";
    PrintList( lst2);
    cout << endl;
    lst1.reverse();
    cout << "9) ";
    PrintList( lst1);
    cout << endl;
    lst2.push_back (100);
    lst2.push_back (200);
    lst2.push_back (300);
    lst2.push_back (400);
    list<A>::iterator p1,p2,p3;
    p1 = find(lst1.begin(),lst1.end(),3);
    p2 = find(lst2.begin(),lst2.end(),200);
    p3 = find(lst2.begin(),lst2.end(),400);
    lst1.splice(p1,lst2,p2, p3);
    cout << "10) ";
    PrintList( lst1);
    cout << endl;
    cout << "11) ";
    PrintList( lst2);
    cout << endl;
    return 0;
}

贪心

　　贪心，一个让本蒟蒻头疼的算法，有时候只需for+while和if-else，有时

的代码行数又让人感动.

　　由于贪心有很多种不同的题型，像DP一样，但也没法像DP一样找出转移方程，所以就不介绍

定义什么的了，原因有两点{

　　1.贪心题型太零散，太碎，不好总结.

　　2.个人水平有限.

　　3.（也是最主要的）现在是北京时间“22：04”，本蒟蒻睁不动眼了（早上4：34起的），但还有许多内容没写完.

}

综合以上几个原因，所以用两个例题来理解.

例题：

1228：书架

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 11146 通过数: 6463

【题目描述】

John最近买了一个书架用来存放奶牛养殖书籍，但书架很快被存满了，只剩最顶层有空余。

John共有 $N$

为了到达书架顶层，奶牛可以踩着其他奶牛的背，像叠罗汉一样，直到他们的总高度不低于书架高度。当然若奶牛越多则危险性越大。为了帮助John到达书架顶层，找出使用奶牛数目最少的解决方案吧。

【输入】

第1行：空格隔开的整数 $N$

第2~N+1行：第 $i + 1$

【输出】

能达到书架高度所使用奶牛的最少数目。

【输入样例】

【输出样例】


这道题思路其实很简单，只要现将奶牛的高度排序，再进行从大到小遍历，if+累加就可以了.

上菜：

#include<bits/stdc++.h>
using namespace std;
int n,a[20001],b;
int cmp(int a,int b){
    return a>b;
}
int main(){
    cin>>n>>b;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1,cmp);
    int ans=0,s=0;
    for(int i=1;i<=n;i++){
        if(s<b){
            ans++;
            s+=a[i];
        }else break;
    }
    cout<<ans<<endl;
    return 0;
}

1322：【例6.4】拦截导弹问题(Noip1999)

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统，但是这种拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，由于该系统还在试用阶段。所以一套系统有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度不大于30000的正整数）。计算要拦截所有导弹最小需要配备多少套这种导弹拦截系统。

【输入】

n颗依次飞来的高度（1≤n≤1000）。

【输出】

要拦截所有导弹最小配备的系统数k。

【输入样例】

389 207 155 300 299 170 158 65

【输出样例】

【提示】

输入：导弹高度： 4 3 2

输出：导弹拦截系统k=1

当我还是蒟蒻中的蒟蒻时，这道题就是噩梦.

但后来会了之后，也没那么难，歇菜：

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int main() {
    int t,r=0,k[N];
    while(cin>>t) {
        int mi=30*N,s;
        for(int i=0; i<r; i++) {
            if(t<=k[i]) {
                if(mi>k[i]-t) {
                    mi=k[i]-t;
                    s=i;
                }
            }
        }
        if(mi<30*N)k[s]=t;
        else k[r++]=t;
    }
    cout<<r;
    return 0;
}

分治

原理：

分而治之，可以将一个大问题转化成多个子问题（快排、归并、二分……）.

例题：

汉诺塔：

只给重点：

void move(int n, char a, char b, char c) {
    if(n > 1) move(n-1, a, c, b);
    if(n > 1) move(n-1, b, a, c);
}
int main() {
    int n;
    scanf("%d", &n);
    move(n,'a','b','c');
    return 0;
}

快排（大到小）：

#include<bits/stdc++.h>
using namespace std;
const int N=10005;
int a[N];
void qsort(int l,int r) {
    if(l>=r) return ;
    int i=l,j=r,temp=a[r];
    while(i<j) {
        while(a[i]<=temp&&i<j) i++;
        a[j]=a[i];
        while(a[j]>=temp&&j>i) j--;
        a[i]=a[j];
    }
    a[i]=temp;
    qsort(l,i-1);
    qsort(i+1,r);
}
int main() {
    int n;
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    for(int i=1;i<=n;i++) printf("%d ",a[i]);    
    return 0;
}

小到大的话，这里可以偷个懒，输出时倒着输出.

归并（从小到大）：

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N];
void merge(int l1,int r1,int l2,int r2){
    int i=l1,j=l2,k=l1,temp[N];
    while(i<=r1&&j<=r2){
        if(a[i]<a[j]){
            temp[k++]=a[i++];
        }else{
            temp[k++]=a[j++];
        }
    }
    while(i<=r1) temp[k++]=a[i++];
    while(j<=r2) temp[k++]=a[j++];
    for(int i=l1;i<=r2;i++){
        a[i]=temp[i];
    }
}
void merge_sort(int l,int r){
    if(l==r) return ;
    int mid=l+(r-l)/2;
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    merge(l,mid,mid+1,r);
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];                                                            
    merge_sort(1,n);
    for(int i=1;i<=n;i++) printf("%d ",a[i]);
    return 0;
}

偷懒技巧同上.

二分算法

二分和分治差不多，不细讲.

需要时有序序列.

三个指针，r，l，mid.

例题：

P2249 【深基13.例1】查找

题目描述

输入 $n(n\le10^6)n(n≤106) 个不超过 10^9109 的单调不减的（就是后面的数字不小于前面的数字）非负整数 a_1,a_2,\dots,a_{n}a1,a2,…,an，然后进行 m(m\le10^5)m(m≤105) 次询问。对于每次询问，给出一个整数 q(q\le10^9)q(q≤109)，要求输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 -1 。$

输入格式

第一行 2 个整数 n 和 m，表示数字个数和询问次数。

第二行 n 个整数，表示这些待查询的数字。

第三行 m 个整数，表示询问这些数字的编号，从 1 开始编号。

输出格式

m 个整数表示答案。

输入输出样例

输入 #1

11 3
1 3 3 3 5 7 9 11 13 15 15
1 3 6

输出 #1

1 2 -1

说明/提示

$10^6106 规模的数据读入，请用 scanf。用 cin 会超时。$

code：

#include<bits/stdc++.h>
using namespace std;
int n,m,q,a[1000005];
int find(int x) { 
    int l=1,r=n;
    while (l<r) {
        int mid=l+(r-l)/2;
        if (a[mid]>=x) r=mid;
        else l=mid+1;
    }
    if (a[l]==x) return l; 
    else return -1;
}
int main() {
    scanf("%d%d",&n,&m); 
    for (int i=1 ; i<=n ; i++) scanf("%d",&a[i]); 
    for (int i=1 ; i<=m ; i++) {
        scanf("%d",&q);
        int ans=find(q); 
        printf("%d ",ans); 
    }
    return 0;
}

posted on 2022-07-26 19:22 博然后深阅读(83) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

2022.7.25学习笔记

主要内容：

单调栈

定义：

特点及分类：

例题：

P5788 【模板】单调栈（https://www.luogu.com.cn/problem/P5788）

题目描述

输入格式

输出格式

输入输出样例

说明/提示

单调队列

定义：

例题：

P1886 滑动窗口 /【模板】单调队列（https://www.luogu.com.cn/problem/P1886）

题目描述

输入格式

输出格式

输入输出样例

说明/提示

前缀和

定义：

差分

STL

定义：

优点：

有了STL，不必再写大多的标准数据结构和算法，并且可获得非常高的性能。

分类：

容器概述：

关联容器:

容器适配器:

顺序容器和关联容器中都有的成员函数:

顺序容器的常用成员函数:

迭代器:

定义一个容器类的迭代器的方法可以是：

访问一个迭代器指向的元素：

algorithm :

算法模拟：

贪心

例题：

1228：书架

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

1322：【例6.4】拦截导弹问题(Noip1999)

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

【提示】

分治

原理：

例题：

快排（大到小）：

归并（从小到大）：

二分算法

例题：

P2249 【深基13.例1】查找

题目描述

输入格式

输出格式

输入输出样例

说明/提示

　　有了STL，不必再写大多的标准数据结构和算法，并且可获得非常高的性能。