动态规划
定义:
1.动态规划(Dynamic Programming 简称DP)是解决“多阶段决策问题”的一种高效算法。
2. 通过合理组合子问题的解从而解决整个问题解。其中的子问题并不是独立的,这些子问题又包含有公共的子子问题.
3.动态规划算法就是对每个子问题只求一次,并将其结果保存在一张表中(数组),以后再用到时直接从表中拿过来使用,避免重复计算相同的子问题.
4.“不做无用功”的求解模式,大大提高了程序的效率.
5. 常用于解决统计类问题(统计方案总数)和最优值问题(最大值或最小值).
步骤:
1.根据时间或空间确定要去的状态.
2.写出动态规划方程.
3.求解:记忆化搜索;递推(倒推或者正推).
常见DP:
1.坐标型.
2.线性型.
3.区间型.
4.背包型.
5.树型.
例题:(01背包||完全背包请看博客文章)
https://www.cnblogs.com/boranhoushen/articles/16268592.html
https://www.cnblogs.com/boranhoushen/articles/16260203.html
1258:【例9.2】数字金字塔
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
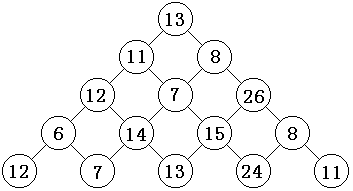
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
【输入】
第一个行包含R(1≤R≤1000)R(1≤R≤1000),表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100100。
【输出】
单独的一行,包含那个可能得到的最大的和。
【输入样例】
5 13 11 8 12 7 26 6 14 15 8 12 7 13 24 11
【输出样例】
86
【代码】:
#include<bits/stdc++.h> using namespace std; int n,a[1001][1001],f[1001][1001]; int main(){ cin>>n; for(int i=1;i<=n;i++){ for(int j=1;j<=i;j++){ cin>>a[i][j]; } } f[1][1]=a[1][1]; for(int i=2;i<=n;i++){ for(int j=1;j<=i;j++){ f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j]; } } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,f[n][i]); cout<<ans; return 0; }
1259:【例9.3】求最长不下降序列
时间限制: 1000 ms 内存限制: 65536 KB【题目描述】
设有由n(1≤n≤200)n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)b(1)、b(2)、……、b(n)若存在i1<i2<i3<…<iei1<i2<i3<…<ie 且有b(i1)<=b(i2)<=…<=b(ie)b(i1)<=b(i2)<=…<=b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为77的不下降序列,同时也有7 ,9,16,18,19,21,22,63组成的长度为88的不下降序列。
【输入】
第一行为n,第二行为用空格隔开的n个整数。
【输出】
第一行为输出最大个数max(形式见样例);
第二行为max个整数形成的不下降序列,答案可能不唯一,输出一种就可以了,本题进行特殊评测。
【输入样例】
14 13 7 9 16 38 24 37 18 44 19 21 22 63 15
【输出样例】
max=8 7 9 16 18 19 21 22 63
【代码】:
#include<bits/stdc++.h> using namespace std; int n,a[1001],f[1001],p[1001],ans; void dfs(int i){ if(p[i]>0) dfs(p[i]); cout<<a[i]<<" "; } int main(){ cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; f[1]=1; p[1]=0; for(int i=2;i<=n;i++) { f[i]=0; for(int j=1;j<=i;j++) if(a[j]<=a[i]&&f[j]>f[i]) { f[i]=f[j]; p[i]=j; } f[i]++; } int ans=0,k=0; for(int i=1;i<=n;i++) if(f[i]>ans) ans=f[k=i]; cout<<"max="<<ans<<endl; dfs(k); return 0; }
1270:【例9.14】混合背包
时间限制: 1000 ms 内存限制: 65536 KB【题目描述】
一个旅行者有一个最多能装V公斤的背包,现在有n件物品,它们的重量分别是W1,W2,...,WnW1,W2,...,Wn,它们的价值分别为C1,C2,...,CnC1,C2,...,Cn。有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
【输入】
第一行:二个整数,M(背包容量,M<=200),N(物品数量,N<=30);
第2..N+1行:每行三个整数Wi,Ci,PiWi,Ci,Pi,前两个整数分别表示每个物品的重量,价值,第三个整数若为0,则说明此物品可以购买无数件,若为其他数字,则为此物品可购买的最多件数(PiPi)。
【输出】
仅一行,一个数,表示最大总价值。
【输入样例】
10 3 2 1 0 3 3 1 4 5 4
【输出样例】
11
【提示】
选第一件物品1件和第三件物品2件。
【代码】:
#include<bits/stdc++.h> using namespace std; const int N=201; int qread () { int x=0,f=1; char ch=getchar(); while (ch>'9'||ch<'0') { if(ch=='-') f=-1; ch=getchar(); } while (ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+ch-48; ch=getchar(); } return x*f; } int i,j,m,n,wi,ci,ti,k,f[N]={0}; int main () { m=qread();n=qread(); for(i=1;i<=n;i++) { wi=qread();ci=qread();ti=qread(); if(ti==0) { for(j=wi;j<=m;j++) if(f[j]<f[j-wi]+ci) f[j]=f[j-wi]+ci; } for(k=1;k<=ti;k++) for(j=m;j>=wi;j--) if(f[j]<f[j-wi]+ci) f[j]=f[j-wi]+ci; } printf("%d",f[m]); return 0; }
1272:【例9.16】分组背包
时间限制: 1000 ms 内存限制: 65536 KB题目描述】
一个旅行者有一个最多能装V公斤的背包,现在有n件物品,它们的重量分别是W1,W2,...,WnW1,W2,...,Wn,它们的价值分别为C1,C2,...,CnC1,C2,...,Cn。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
【输入】
第一行:三个整数,V(背包容量,V≤200),N(物品数量,N≤30)和T(最大组号,T≤10);
第2..N+1行:每行三个整数Wi,Ci,PWi,Ci,P,表示每个物品的重量,价值,所属组号。
【输出】
仅一行,一个数,表示最大总价值。
【输入样例】
10 6 3 2 1 1 3 3 1 4 8 2 6 9 2 2 8 3 3 9 3
【输出样例】
20
【代码】:
#include<bits/stdc++.h> using namespace std; int V,N,T; int w[31]; int c[31]; int p[11][31]; int dp[201]; int main(){ cin>>V>>N>>T; for(int i=1;i<=N;i++){ int t; cin>>w[i]>>c[i]>>t; int len=sizeof(p[t])/sizeof(int); for(int j=1;j<=len;j++){ if(p[t][j]==0){ p[t][j]=i; break; } } } for(int i=1;i<=T;i++){ for(int j=V;j>=0;j--){ int len=sizeof(p[i])/sizeof(int); for(int k=1;k<=len;k++){ if(j>=w[p[i][k]]) dp[j]=max(dp[j],dp[j-w[p[i][k]]]+c[p[i][k]]); } } } cout<<dp[V]<<endl; return 0; }
1274:【例9.18】合并石子
时间限制: 1000 ms 内存限制: 65536 KB【题目描述】
在一个操场上一排地摆放着N堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的得分。
计算出将N堆石子合并成一堆的最小得分。
【输入】
第一行为一个正整数N (2≤N≤100);
以下N行,每行一个正整数,小于10000,分别表示第i堆石子的个数(1≤i≤N)。
【输出】
一个正整数,即最小得分。
【输入样例】
7 13 7 8 16 21 4 18
【输出样例】
239
【代码】:
#include<bits/stdc++.h> using namespace std; int min(int a,int b){return a>b ? b:a;} int f[101][101],s[101],n,k,x; int main(){ cin>>n; for(int i=1; i<=n; i++) { cin>>x; s[i]=s[i-1]+x; } memset(f,127/3,sizeof(f)); for(int i=1;i<=n;i++) f[i][i]=0; for(int i=n-1;i>=1;i--){ for(int j=i+1;j<=n;j++){ for(int k=i;k<=j-1;k++){ f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]); } } } cout<<f[1][n]; return 0; }
1281:最长上升子序列
时间限制: 1000 ms 内存限制: 65536 KB题目描述】
一个旅行者有一个最多能装V公斤的背包,现在有n件物品,它们的重量分别是W1,W2,...,WnW1,W2,...,Wn,它们的价值分别为C1,C2,...,CnC1,C2,...,Cn。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
【输入】
第一行:三个整数,V(背包容量,V≤200),N(物品数量,N≤30)和T(最大组号,T≤10);
第2..N+1行:每行三个整数Wi,Ci,PWi,Ci,P,表示每个物品的重量,价值,所属组号。
【输出】
仅一行,一个数,表示最大总价值。
【输入样例】
7 1 7 3 5 9 4 8
【输出样例】
4
【代码】:
#include<bits/stdc++.h> using namespace std; int n,a[1001],f[1001],ans; int main(){ cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; f[1]=1; for(int i=2;i<=n;i++){ f[i]=0; for(int j=1;j<=i;j++) if(a[j]<a[i]) f[i]=max(f[i],f[j]); f[i]++; } ans=0; for(int i=1;i<=n;i++) ans=max(ans,f[i]); cout<<ans<<endl; return 0; }
1265:【例9.9】最长公共子序列
时间限制: 1000 ms 内存限制: 65536 KB【题目描述】
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X=<x1,x2,…,xm>X=<x1,x2,…,xm>,则另一序列Z=<z1,z2,…,zk>Z=<z1,z2,…,zk>是X的子序列是指存在一个严格递增的下标序列<i1,i2,…,ik><i1,i2,…,ik>,使得对于所有j=1,2,…,k有:
Xij=ZjXij=Zj
例如,序列Z=<B,C,D,B>是序列X=<A,B,C,B,D,A,B>的子序列,相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例如,若X=<A,B,C,B,D,A,B>和Y=<B,D,C,A,B,A>,则序列<B,C,A>是X和Y的一个公共子序列,序列 <B,C,B,A>也是X和Y的一个公共子序列。而且,后者是X和Y的一个最长公共子序列.因为X和Y没有长度大于4的公共子序列。
给定两个序列X=<x1,x2,…,xm>X=<x1,x2,…,xm>和Y=<y1,y2….yn>Y=<y1,y2….yn>.要求找出X和Y的一个最长公共子序列。
【输入】
共有两行。每行为一个由大写字母构成的长度不超过1000的字符串,表示序列X和Y。
【输出】
第一行为一个非负整数。表示所求得的最长公共子序列的长度。若不存在公共子序列.则输出文件仅有一行输出一个整数0。
【输入样例】
ABCBDAB BDCABA
【输出样例】
4
【提示】
最长公共子串(Longest Common Substirng)和最长公共子序列(Longest Common Subsequence,LCS)的区别为:子串是串的一个连续的部分,子序列则是从不改变序列的顺序,而从序列中去掉任意的元素而获得新的序列;也就是说,子串中字符的位置必须是连续的,子序列则可以不必连续。字符串长度小于等于1000。
【代码】:
#include<bits/stdc++.h> using namespace std; const int MAXN = 5005; string X,Y; int f[MAXN][MAXN]; int main(){ cin>>X>>Y; int n=X.length(),m=Y.length(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ f[i][j]=max(f[i-1][j],f[i][j-1]); if(X[i-1]==Y[j-1]) f[i][j]=max(f[i][j],f[i-1][j-1]+1); } cout<<f[n][m]<<endl; return 0; }
DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP DP





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现