Hello!大家好,今天继续给大家带来一道动态规划的题目:
1268:【例9.12】完全背包问题
时间限制: 1000 ms 内存限制: 65536 KB提交数: 25172 通过数: 13449
【题目描述】
设有nn种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为MM,今从nn种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于MM,而价值的和为最大。
【输入】
第一行:两个整数,MM(背包容量,M≤200M≤200)和NN(物品数量,N≤30N≤30);
第2..N+12..N+1行:每行二个整数Wi,CiWi,Ci,表示每个物品的重量和价值。
【输出】
仅一行,一个数,表示最大总价值。
【输入样例】
10 4 2 1 3 3 4 5 7 9
【输出样例】
max=12
【题目分析】
(只分析重点部分)
这道题也是开一个二维数组:
状态变量:f[i][j]表示前i件物品放入容量为j的背包的最大价值。
当前背包容量为j,我们要考虑第i件物品能否放入?是否放入?
第一种情况:
当前背包容量j<w[i],不能放入,则f[i][j]=f[i-1][j]。
第二种情况:
当前背包容量j>=w[i],能放入,但要考虑代价大小
(1) 若第i件物品不放入背包,则f[i][j]=f[i-1][j]。
(2) 若第i件物品放入背包,则f[i][j]=f[i][j-w[i]]+c[i]。
对于前i件物品,背包容量为j-w[i]时可能已经放入了第i件物品,容量为j时还可以再放入第i件物品,所以用f[i][j-w[i]]更新f[i][j]。
举个栗子:
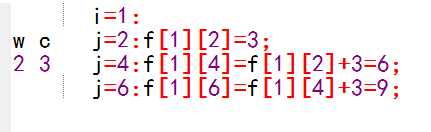
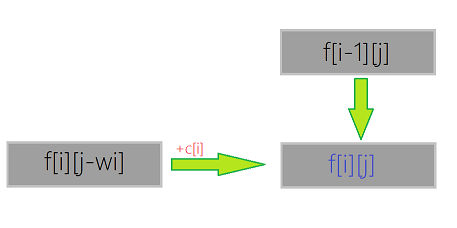
由此可得转移方程:
f[i][j]=f[i-1][j],(j<w[i]);
f[i][j]=max(f[i-1][j],f[i][j-w[i]]+c[i]),(j>=w[i]);
后面就不难了。
【代码思路】
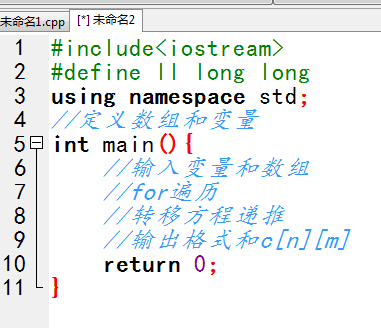
【参考代码】
(保护知识产权,严禁抄袭)
(本题代码已在一本通上通过)
#include<iostream> #define ll long long using namespace std; ll a[10001],b[10001],c[10001][10001]; int main(){ int n,m; cin>>m>>n; for(int i=1;i<=n;i++){ cin>>a[i]>>b[i]; } for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(j<a[i]){ c[i][j]=c[i-1][j]; }else{ c[i][j]=max(c[i-1][j],c[i][j-a[i]]+b[i]); } } } cout<<"max="<<c[n][m]; return 0; }
《 再 见 ! ! ! 》



