F.binary_cross_entropy_with_logits函数与F.binary_cross_entropy函数的关系（二分类问题）
二元交叉熵（Binary cross entropy）是二分类中常用的损失函数，它可以衡量两个概率分布的距离，二元交叉熵越小，分布越相似，其公式如下：
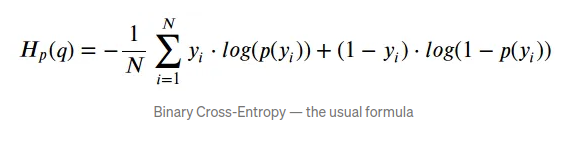
我们用jupyter notebook举例解释一下，
假设 1个图像样本由神经网络处理后的输出是 size 10×4 的tensor，随机生成一个tensor，
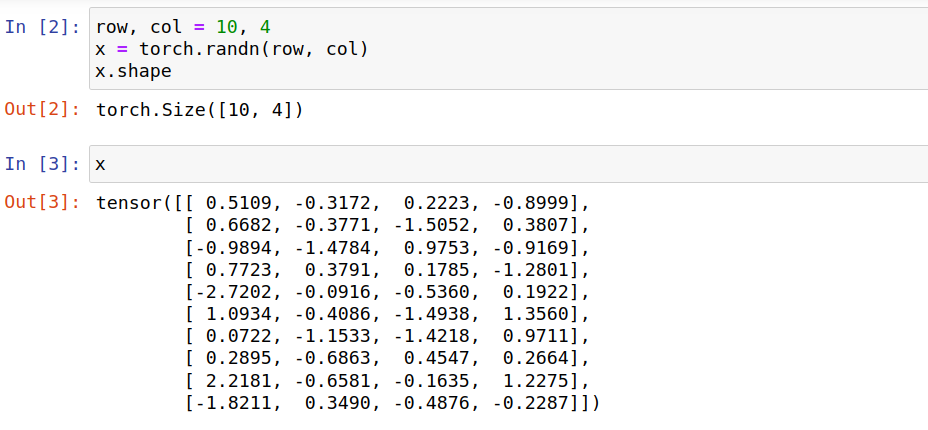
使用Sigmoid对该tensor进行概率变换，tensor的每个数值的变换都是相互独立的，下面得出预测的概率分布，
我们在这里随机生成一个真值的概率分布y，
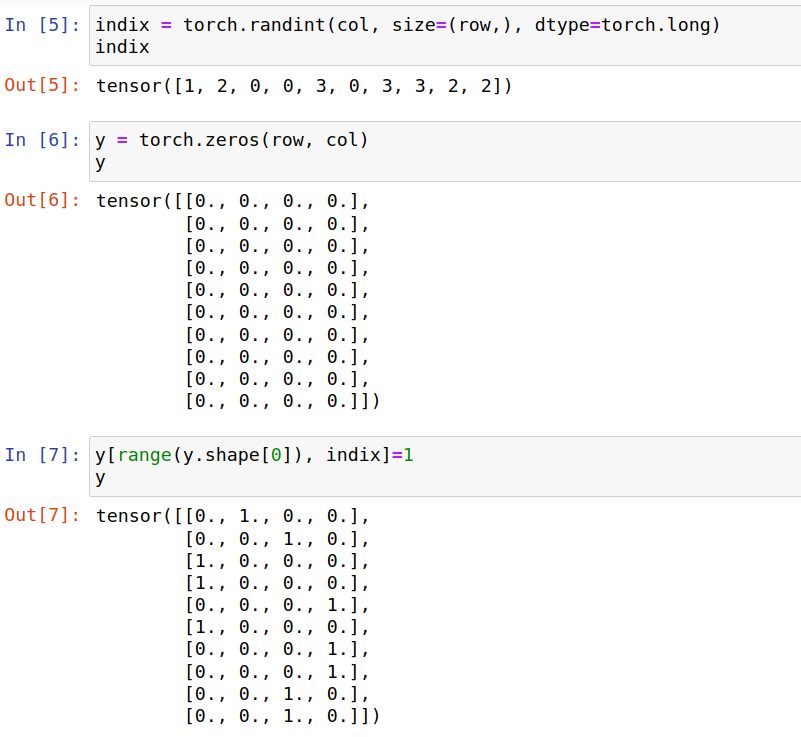
自己定义一下BCELoss，需要输入预测的概率分布和真值的概率分布，BCELoss对每一对概率值（probm,n，ym,n）单独计算交叉熵，然后求和，再求平均，
手动计算一下，结果一致，
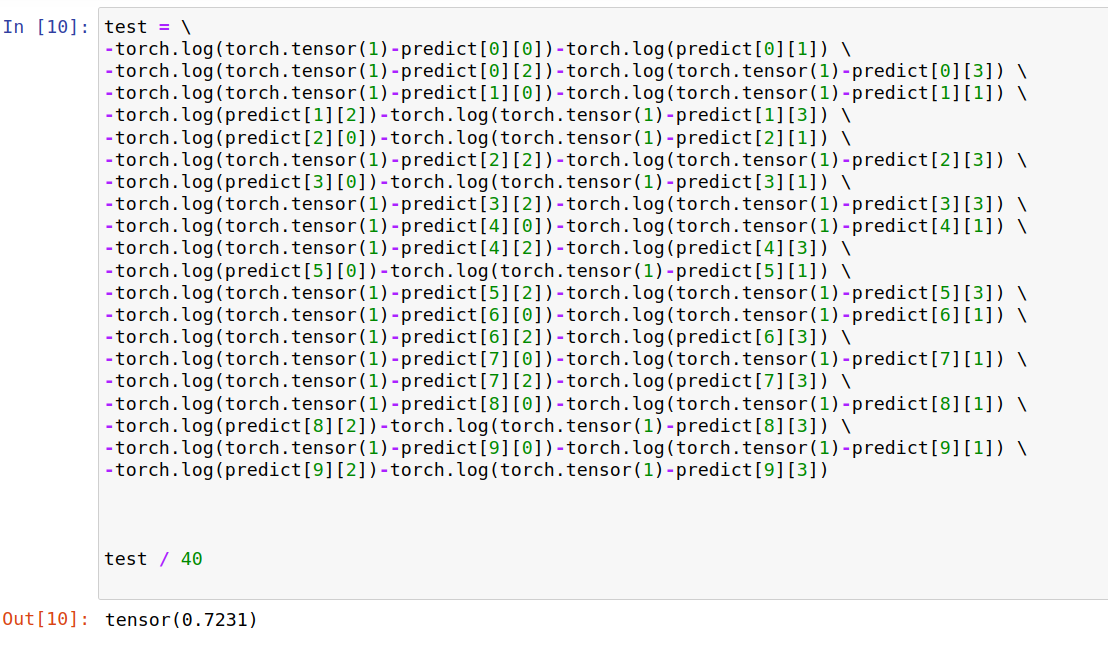
使用F.binary_cross_entropy 验证一下，同样需要输入预测的概率分布和真值的概率分布，
再使用F.binary_cross_entropy_with_logits验证一下，直接输入神经网络的输出和真值的概率分布，
相比F.binary_cross_entropy函数，F.binary_cross_entropy_with_logits函数在内部使用了sigmoid函数，也就是
F.binary_cross_entropy_with_logits = sigmoid + F.binary_cross_entropy。
实际使用时：
假设输入神经网络的batch_size= 8，每个图像样本经过处理后的输出是 size = 10×4 的tensor，每个 tensor 被看作 40 个样本点的集合，那么 8个图像样本得到 320个样本点，
F.binary_cross_entropy_with_logits函数和 F.binary_cross_entropy函数的 reduction 参数都默认是‘mean’模式，直接使用默认值的话，结果是320个样本点的二元交叉熵的平均值，
若要计算8个图像样本的二元交叉熵的平均值，可以设置 reduction=‘sum’ ， 这样能得到 320个样本点的二元交叉熵的和，然后除以batch_size 就能得到8个图像样本的二元交叉熵的平均值，
loss = F.binary_cross_entropy_with_logits(predict, y, weight, reduction='sum') / batch_size
这里的predict 和 y都是 8×10×4 的shape。
BCELoss与BCEWithLogitsLoss的关联：BCEWithLogitsLoss = Sigmoid + BCELoss，
注：术语 cross-entropy loss 与 log loss（或称 logistic loss or logarithmic loss）可以互换使用。
Enjoy it!
