深度学习中的激活函数之 sigmoid、tanh和ReLU

 

 

 

三种非线性激活函数sigmoid、tanh、ReLU。

sigmoid： y = 1/(1 + e^-x)

tanh： y = (e^x - e^-x)/(e^x + e^-x)

ReLU：y = max(0, x)

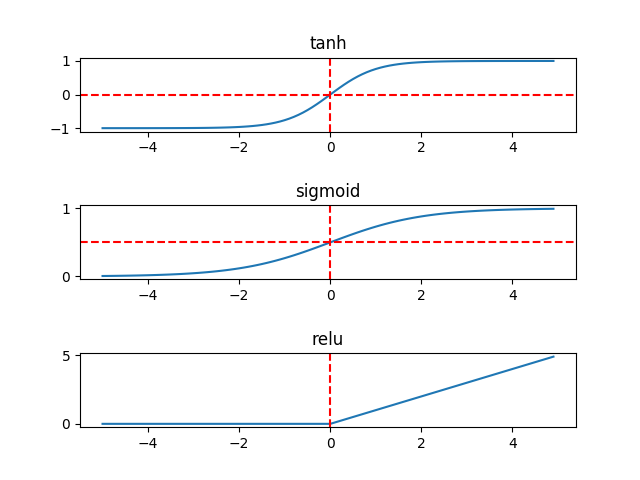
在隐藏层，tanh函数要优于sigmoid函数，可以看作是sigmoid的平移版本，优势在于其取值为 [-1, 1]，数据的平均值为0，而sigmoid的平均值为0.5，有类似数据中心化的效果。

但在输出层，sigmoid可能会优于tanh，原因在于我们希望输出结果的概率落在0~1之间，比如二元分类问题，sigmoid可以作为输出层的激活函数。

在实际情况中，特别是在训练深层网络时，sigmoid和tanh会在端值趋近饱和，造成训练速度减慢，故深层网络的激活函数多是采用ReLU，浅层网络可以采用sigmoid和tanh函数。

 

为弄清在反向传播中如何进行梯度下降，来看一下三个函数的求导过程：

1. sigmoid求导

sigmoid函数定义为  y = 1/(1 + e^-x)  = (1 + e^-x)^-1

相关的求导公式：(xⁿ)' = n * x^n-1   和  (e^x)^' = e^x

应用链式法则，其求导过程为：

                                                        dy/dx = -1 * (1 + e-x)-2 * e-x * (-1)

                                                     = e-x * (1 + e-x)-2

                                                     = (1 + e-x - 1) / (1 + e-x)2

                                                     = (1 + e-x)-1 - (1 + e-x)-2
                                                     = y - y2
                                                     = y(1 -y)

2. tanh求导

tanh函数定义为 y = (e^x - e^-x)/(e^x + e^-x)

相关的求导公式：(u/v)^' = (u^' v - uv^') / v² 

应用链式法则，其求导过程为：

                                                                dy/dx = ( (e^x - e^-x)^' * (e^x + e^-x) - (e^x - e^-x) * (e^x + e^-x)^' ) / (e^x + e^-x)² 

　　　　　　　　　　　　　　　　             =  ( (e^x - (-1) * e^-x) * (e^x + e^-x) - (e^x - e^-x) * (e^x + (-1) * e^-x) ) / (e^x + e^-x)² 　　

　　　　　　　　　　　　　　　　             =  ( (e^x + e^-x)²  -  (e^x - e^-x)² ) / (e^x + e^-x)² 

　　　　　　　　　　　　　　　　             =  1 -  ( (e^x - e^-x)/(e^x + e^-x) )² 

　　　　　　　　　　　　　　　　             = 1 - y² 

3. ReLU求导

ReLU函数定义为 y = max(0, x)

简单地推导得 当x <0 时，dy/dx = 0; 当 x >= 0时，dy/dx = 1

 

接下来着重讨论下ReLU

在深度神经网络中，通常选择线性整流函数（ReLU，Rectified Linear Units）作为神经元的激活函数。ReLU源于对动物神经科学的研究，2001年，Dayan 和 Abbott 从生物学角度模拟出了脑神经元接受信号更精确的激活模型，如图：

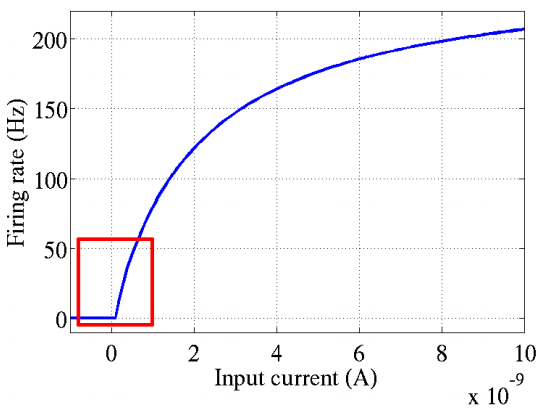
其中横轴是刺激电流，纵轴是神经元的放电速率。同年，Attwell等神经学科学家通过研究大脑的能量消耗过程，推测神经元的工作方式具有稀疏性和分布性；2003年，Lennie等神经学科学家估测大脑同时被激活的神经元只有1~4%，这进一步表明了神经元工作的稀疏性。

那么，ReLU是如何模拟神经元工作的呢

 

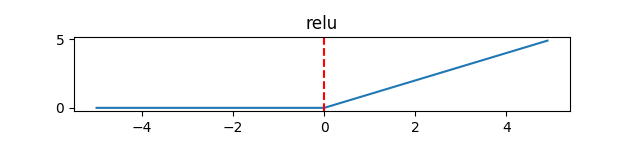
从上图可以看出，ReLU其实是分段线性函数，把所有的负值都变为0，正值不变，这种性质被称为单侧抑制。因为单侧抑制的存在，才使得神经网络中的神经元也具有了稀疏激活性。尤其在深度神经网络中（如CNN），当模型增加N层之后，理论上ReLU神经元的激活率将降低2的N次方倍。或许有人会问，ReLU的函数图像为什么非得长成这样子。其实不一定这个样子。只要能起到单侧抑制的作用，无论是镜面翻转还是180°翻转，最终神经元的输入也只是相当于加上了一个常数项系数，并不会影响模型的训练结果。之所以这样定义，或许是为了符合生物学角度，便于我们理解吧。

这种稀疏性有什么作用呢？因为我们的大脑工作时，总有一部分神经元处于活跃或抑制状态。与之类似，当训练一个深度分类模型时，和目标相关的特征往往也就几个，因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征，使网络拟合训练数据。

相比其他激活函数，ReLU有几个优势：（1）比起线性函数来说，ReLU的表达能力更强，尤其体现在深度网络模型中；（2）较于非线性函数，ReLU由于非负区间的梯度为常数，因此不存在梯度消失问题（Vanishing Gradient Problem），使得模型的收敛速度维持在一个稳定状态。（注）梯度消失问题：当梯度小于1时，预测值与真实值之间的误差每传播一层就会衰减一次，如果在深层模型中使用sigmoid作为激活函数，这种现象尤为明显，将导致模型收敛停滞不前。