使用滚动平均实现平滑数据

使用滚动平均实现平滑数据

时间序列数据通常包含一些噪声。而去除噪声最简单的方式就是使用一种简单的一致核来平滑数据。这种方式也叫滚动平均。
卷积是组合两个数组的一种数学运算，其中一个数组是我们的数据，通过一个核数组对其进行卷积。在卷积过程中，将核集中在一个数据点上。
然后将核中的每个数据点与每个相应的数据点相乘，将所有的结果加起来，形成新的数据点。
实例：

data = [2, 3, 1, 4, 1]
kernel = [1, 2, 3, 4]
np.convolve(data, kernel)
结果：# array([ 2,  7, 13, 23, 24, 18, 19,  4])

下面将计算过程一步一步细化：
首先，np.convolve会翻转kernel得到flipped kernel [4, 3, 2, 1]

[4, 3, 2, 1]  # The flipped kernel
          x
         [2, 3, 1, 4, 1]  # The data
          2= 2
         [2]
 
   [4, 3, 2, 1]
          x  x
         [2, 3, 1, 4, 1]
          4+ 3= 7
         [2, 7]
 
      [4, 3, 2, 1]
          x  x  x
         [2, 3, 1, 4, 1]
          6+ 6+ 1=13
         [2, 7, 13]
 
         [4, 3, 2, 1]
          x  x  x  x
         [2, 3, 1, 4, 1]
          8+ 9+ 2+ 4= 23
         [2, 7,13, 23]
             [4, 3, 2, 1]
              x  x  x  x
          [2, 3, 1, 4, 1]
             12+ 3+ 8+ 1 = 24
                [4, 3, 2]
                 x  x  x
          [2, 3, 1, 4, 1]
                 4+ 12+ 2 = 18
                   [4, 3]
                    x  x
          [2, 3, 1, 4, 1]
                    16+ 3 = 19
                       [4]
                        x
          [2, 3, 1, 4, 1]
                        4

方法np.convolve的一般语法是np.convolve(data, kernel, mode='valid'), 这里的mode决定了边界的取舍, 默认mode='full'。

• mode='valid': 将不匹配完全kernel的数据的边界全部去掉,在实例中也就是kernel的长度是4，那么数据也要取4，其余的数据不要。
• mode='same': 新生成的数组与原数组的形状一致，也就是说，新生成的数组和原数组维度一致。
• mode='full': 边界不省略，保留全部计算。

实例：

data = [2, 3, 1, 4, 1]
kernel = [1, 2, 3, 4]
np.convolve(data, kernel, mode='valid')
结果：# array([23, 24])

实例：

data = [2, 3, 1, 4, 1]
kernel = [1, 2, 3, 4]
np.convolve(data, kernel, mode='same')
结果：# array([ 7, 13, 23, 24, 18])

小tips ： 最好对kernel进行归一化，原因在于如果不进行归一化，有可能导致原始信号的量纲变得很大，导致不可想象的错误。此外，kernel的大小也对卷积效果有影响。

实例：

kernel_size = 10
kernel = np.ones(kernel_size) / kernel_size
data_convolved_10 = np.convolve(data, kernel, mode='same')
 
kernel_size = 20
kernel = np.ones(kernel_size) / kernel_size
data_convolved_20 = np.convolve(data, kernel, mode='same')
 
plt.plot(data_convolved_20)
plt.plot(data_convolved_10)
plt.legend(("Kernel Size 10", "Kernel Size 20"))

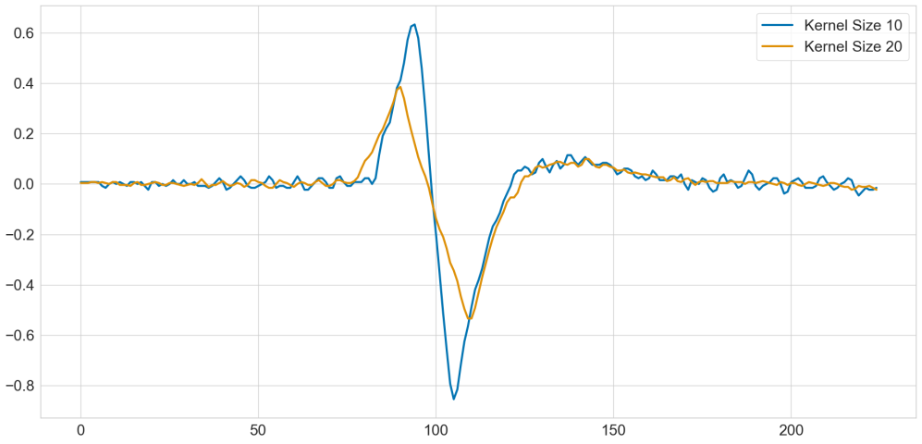
结论：较大的核会导致较小的尖峰，波峰也会改变。具体来说，滚动均值是一个低通滤波器，这意味着它使低频信号单独存在，而使高频信号更小。数据的急剧增加具有很高的频率。如果我们使核更大，滤波器对高频信号的衰减会更大。
这就是滚动平均的工作原理。它消除了高频噪声。这也意味着我们必须小心，不要用滚动平均滤波器过多地扭曲信号。