回归分析-线性回归

使用kaggle比赛中的公开数据IceCreamData数据来完成温度和销售利润的线性关系。本实例使用python来仿真实现。

1. 下载数据，IceCreamData需要注册和下载到本地。大体背景是你拥有一家冰淇淋公司，你想创建一个模型，可以根据外部空气温度(度)预测每天的收入。

2. 导入数据

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(theme='grade3',context='notebook',ticks=True,grid=False)
sales_df = pd.read_csv('yourpath/IceCreamData.csv')
sales_df.shape

3. 分析数据

拿到数据之后，首先需要对数据进行理解和分析，可视化是较为有效的技术手段。当然一些基本的统计或者观察也不可缺少。

• 查看数据基本信息

sales_df.info()

• 查看数据统计值

sales_df.describe() # 查看数据的一些统计信息，如最大、最小、均值、反差

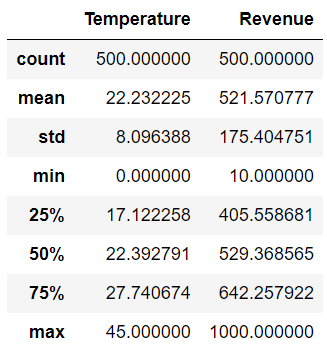
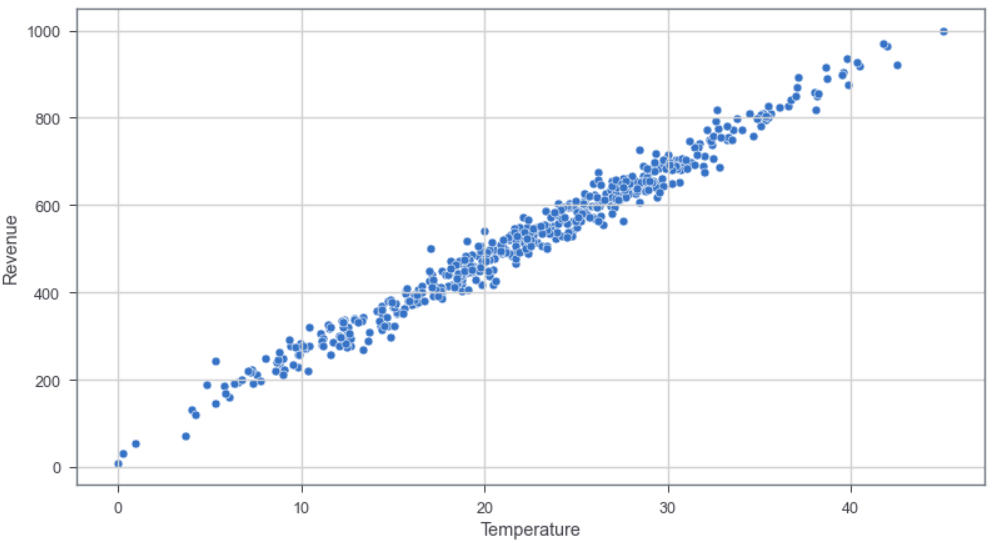
• 查看数据：可视化看散点分布

plt.figure(figsize=(13,7))
sns.scatterplot(x='Temperature',y='Revenue',data=sales_df) #绘制散点图
plt.grid()

• 查看数据：可视化看散点分布与正态分布图

sns.jointplot(x='Temperature',y='Revenue',data=sales_df)
plt.grid()

• 查看数据：可视化散点图与正态分布图

sns.pairplot(sales_df)
plt.rcParams['font.sans-serif']=['SimHei']
plt.grid()
plt.suptitle('散点图和正态分布图',fontsize=20) 

• 查看数据：使用直线拟合可视化

plt.figure(figsize=(13,7))
sns.regplot(x='Temperature',y='Revenue',data=sales_df)
plt.grid()

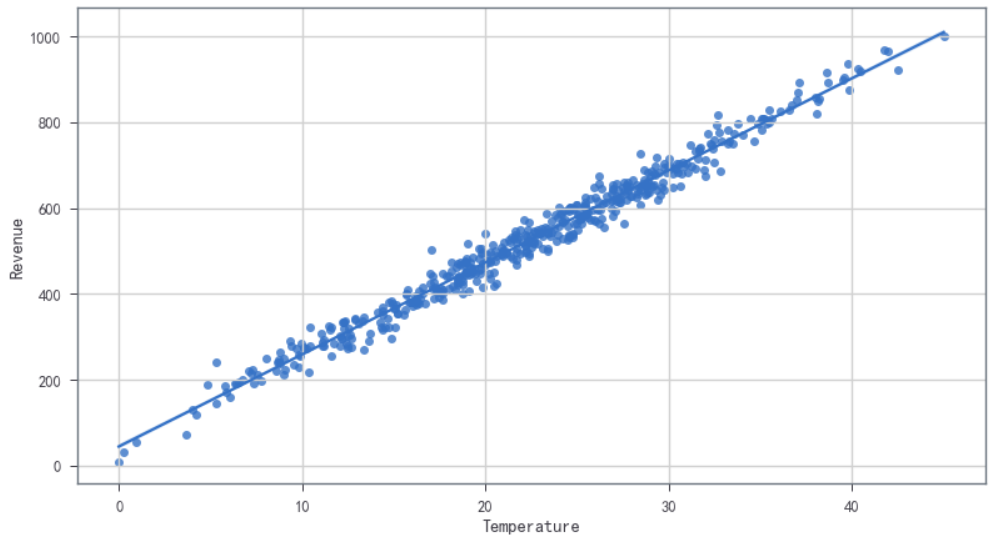
小结：从上述的数据查看可视化，数据分析看，线性回归模型就能以后不错的回归效果

4. 数据处理和线性回归模型建模

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X = sales_df['Temperature']
y = sales_df['Revenue']

X = np.array(X) # 将pandas的series类型转化为Numpy的Array(数组)
y = np.array(y)
X = X.reshape(-1, 1) # 将X数组重新构建为500行，1列
y = y.reshape(-1, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2) #训练集和测试集的分割
SimpleLinearRegression = LinearRegression(fit_intercept=True)
SimpleLinearRegression.fit(X_train, y_train)
print('Linear Model Coeff(m)%.2f'%SimpleLinearRegression.coef_)
print('Linear Model Coeff(b)%.2f'%SimpleLinearRegression.intercept_)

获得了m值和b值，即斜率是21.44，截距是45.66

• 对训练集的数据，可视化温度和销售收入之间的回归曲线

# 得到散点图
plt.scatter(X_train, y_train, color='green')
# 得到预测的销售收入，与实际温度之间的线性回归曲线
plt.plot(X_train, SimpleLinearRegression.predict(X_train),color='blue')
# 设置x,y坐标轴的名称
plt.ylabel('Revenue[$]')
plt.xlabel('Temperature[DegC]')
# 设置图形标题
plt.title('Revenue Generated vs. Temperature')

• 查看训练集的温度和销售收入的相关系数

accuracy_LinearRegression = SimpleLinearRegression.score(X_train,y_train)
accuracy_LinearRegression

结果：0.9792858307245188

• 查看测试集的温度与销售收入的回归关系

plt.scatter(X_test,y_test,color='red')
plt.plot(X_test, SimpleLinearRegression.predict(X_test),color='blue')
plt.ylabel('Revenue[$]')
plt.xlabel('Temperature[DegC]')
plt.title('Revenue Generated vs. Temperature')

• 查看测试数据集的温度与销售收入的相关系数

pre_LinearRegression = SimpleLinearRegression.score(X_test,y_test)
pre_LinearRegression

结果：0.9808887231054377

5. 线性回归模型的优劣分析

import statsmodels.api as sm
X2 = sm.add_constant(X_train)
est = sm.OLS(y_train, X2).fit()
print(est.summary())

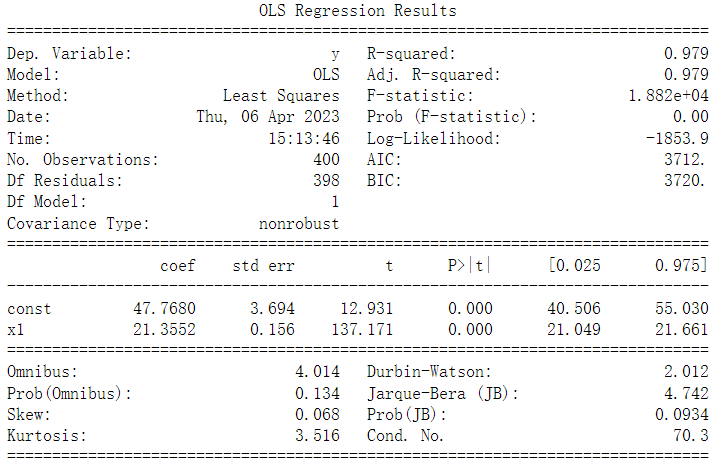
对于模型评估而言，通常需要关心上图中的R-squared、Adj.R-squared和P值信息。这里的R-squared为0.979，Adj.R-squared为0.979，
说明模型的线性拟合程度较高；这里的P值有两个，常数项（const）和特征变量（温度）的P值都约等于0<0.05，所以这两个变量都和目标变量（收入）显著相关，即真的具有相关性，而不是由偶然因素导致的。

对于上图的参数的一些详细解释

• Dependent variable（因变量）：因变量是依赖其他变量的变量。在这里y是因变量，y依赖x 。
• Model（模型）：最小二乘法是使用最为广泛的方法。该模型给出了真实总体回归线的最佳近似。OLS的原理是最小化误差的平方\(argmin \sum e_{i}^{2}\)
• Method：表示最小二乘法
• Date:日期
• Time：时间
• Number of observations(样本数)：观察的次数就是样本的大小
• Degree of freedom(df) of residuals（残差自由度）：自由度是计算平方和所依据的独立观测的数量。D.f Residuals = 400 - 1 - 1 = 398, Degrees of freedom, D.f = N – K, N为样本数，K为变量数 + 1
• Df of model: 模型自由度，Df of model = K – 1 = 2 – 1 = 1
• Covariance Type：协方差类型通常是非鲁棒的，这意味着不需要消除数据来计算特征之间的协方差。协方差显示两个变量如何相对于彼此移动。
• R–squared value: \(R^{2}\)是决定系数，是提供有关模型拟合优度的信息的度量。这里，\(y\)的97.9%的变化可以用x来解释，\(R^{2}\)的最大可能值可以是1，意味着\(R^{2}\)值越大回归效果越好。

\[\begin{equation} R^{2} = 1-\frac{sum squared regression(SSR)}{total sum of squares(SST)}\\ = 1 - \frac{\sum (y_{i}-\hat{y_{i}})^{2}}{\sum (y_{i}-\bar{y})^{2}}\notag % \notag 取消编号 \end{equation} \]

• Adj. R-squared（Adjusted R-Squared）：修正R-squared基于模型中独立变量的个数来调整统计值。\(R^{2}\)表示数据点拟合曲线或直线的拟合程度。Adjusted R-Squared也表示数据点拟合曲线或直线的拟合程度，但是会根据模型中的数据点进行调整。如果增加更多的无用变量给模型，adjusted r-squared就会下降。如果增加更多有用的变量，adjusted r-squared会增加。
  \(R_{adj}^{2} = 1 - [\frac{(1-R^{2} (n-1))}{n-k-1}]\)，其中n为样本数，k为独立回归子的数量，即模型中变量的数量，不包括常量。也就是Df of model，这里是1。
• F–statistic：F检验表示回归的拟合优度。这个检验类似于t检验或我们对假设做的其他检验。F统计量的计算方法如下:
  \(F = \frac{R^{2}/(k-1)}{(1-R^{2})/(n-k}\),带入\(R^{2}\), \(n\), \(k\), \(F = (0.979/1)/(0.021/398) = 1.882e+04\)
• Prob(F-statistic)：F统计和Prob(F)检验回归模型的总体显著性。检验了所有回归系数都等于零的零假设。 Prob(F)的值是完整模型的零假设为真的概率（即，所有回归系数都为零）。例如，如果Prob(F)的值为0.01000，则100中有1次机会所有回归参数都为零。
• Log-Likelihood：似然法是衡量特定模型与数据拟合程度的一种度量。它解释了参数\(\theta\)解释观察到的数据的好坏。log似然函数类似。公式如下：

\[\begin{equation} ln[f(x_{1})*f(x_{2})*...*f(x_{n})]\\ =\sum_{i=1}^{n}ln[f(x_{i})]\notag \end{equation} \]

• AIC(Akaike Information Criterion): Akaike信息标准是根据模型的最大对数似然性和用于达到该似然性的参数数量（K）计算的。\(AIC = 2k - 2(log-likelihood)\) 给定任何两个估计模型，首选AIC值较低的模型；较低的AIC意味着解释变量较少，拟合更好，或两者兼而有之。
• BIC(Bayesian Information Criterion):Schwarz的贝叶斯信息标准（BIC）是一个模型选择工具。如果模型是在特定数据集（训练集）上估计的，则BIC评分给出了新的数据集（测试集）上模型性能的估计。\(BIC = k*ln(n) - 2*(log-likelihood)\)，给定任何两个估计模型，首选BIC值较低的模型；较低的BIC意味着解释变量较少，拟合更好，或两者兼而有之。
• Constant term: 常数项是回归线的截距 y = mx + b中的b
• Coefficient term:系数项表示y的变化与X的单位变化，即如果X上升1个单位，则y上升21.3552。
• Standard error of parameters:标准误差也称为标准偏差。标准误差显示了这些参数的抽样可变性。
  截断参数的标准误差：\(se(b_{1}) = \sqrt{(\frac{\sum x_{i}^{2}}{n\sum (x_{i}-\bar{x} )^{2}} )\sigma ^{2}}\)
  系数项（斜率）标准误差：$se(b_{2}) = \sqrt{\frac{\sigma^{2} }{\sum (x_{i} - \bar{x} ) } } $， \(\sigma^{2}\)为回归标准误差（SER），且\(\sigma^{2}\)等于剩余平方和（Residual Sum Of Square，RSS，就是\(\sum e_{i}^{2}\)）
• t–statistics: 理论上，我们假设误差项服从正态分布，因此参数\(b_{1}\)和\(b_{2}\)也具有正态分布。
  • \(b_{1} \sim N(B_{1}, \sigma_{b1}^{2})\)
  • \(b_{2} \sim N(B_{1}, \sigma_{b2}^{2})\) \(B_{1}\)和\(B_{2}\)分别为\(b_{1}\)和\(b_{2}\)的均值
    t-统计的计算根据以下假设：
  • \(H_{0}：B_{2} = 0\) 变量X对y没影响
  • \(H_{1}：B_{2} \ne 0\) 变量X对y有影响
    计算t-统计：
    \(t = (b_{1} - B_{1})/se(b_{1})\)
    对于上面的汇总表格，\(b_{1} = 47.7680\)，\(se(b_{1}) = 3.694\), 因此\(t = (47.7680 - 0)/3.694 = 12.931\),类似地，可以计算\(b_{2}\)的t-统计 = 137.171
• p – values: 理论上，我们读到p值是获得t统计量至少与H0相矛盾的概率，因为假设零假设是正确的。在汇总表中，我们可以看到两个参数的p值都等于0。
  这不是确切的0，但由于我们有非常大的统计量(12.931和137.171)p-value将近似为0。
• Confidence intervals:有很多方法来检验这个假设，包括上面提到的p值方法。置信区间法就是其中之一。5%是得出C.I.的标准显著性水平(\(\propto\))。\(B_{1}\)的置信区间是\((b_{1}-t_{\propto /2}se(b_{1}), b_{1}+t_{\propto /2}se(b_{1}))\)。通过查表计算\(b_{1}\)置信区间是（40.506 ，55.030），同理可以得到\(b_{2}\)的置信区间。
• Omnibus：D’Angostino’s test，它提供了一个联合统计检验，以确定是否存在偏斜和偏峰。Omnibus检验的公式\(K = Z_{1}(g_{1})^{2} + Z_{2}(g_{2})^{2}\)。式中Z1和Z2是两个正态化函数，g1和g2则分别是偏度和峰度，
  在Z1和Z2的作用下，K的结果就接近于卡方分布，我们就能用卡方分布来检验了。
• Prob(Omnibus): 将上面的统计数据变成概率
• Skew（Skewness）：关于平均值的数据对称性的度量。正态分布的误差应对称分布在平均值周围（线上下相等）。
  \(Skew(X) = E[(\frac{X-\mu }{\sigma } )^{3}] = \frac{EX^{3}-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}\)
• Kurtosis：分布形状的度量。比较接近平均值的数据量和远离平均值的数据量（在尾部）。
  \(Kurt(X) = E[(\frac{X-\mu }{\sigma })^{4}] = \frac{E[(X-\mu )^{4}]}{(E[(X-\mu)^{2}])^{2}}\)
• Durbin-Watson：是用来检验回归分析中残差的一阶自相关性的(尤其针对时间序列数据).DW检验是一种检验线性回归模型残差自相关性的方法，它基于对残差的一阶差分进行假设检验。当DW检验结果显著大于或小于2时，说明残差存在自相关性，DW统计量的取值范围是[0, 4]，DW=2时表示不存在自相关性
• Jarque-Bera (JB)：Jarque-Bera检验的公式\(JB = \frac{n}{6} (g_{1}^{2} +\frac{1}{4}g_{2}^{2})\)。与Omnibus检验类似，这两个检验都是基于所用数据是正态分布的，即有如下假设。Jarque–Bera检验。如果统计量\(\gg 0\)，则表示数据不是正态分布。
  原假设H0：数据是正态分布的。
  备择假设H1：数据不是正态分布。
• Prob(JB):JB统计量的概率形式
• Cond. No. :条件数。用于诊断多重共线性

6. 线性回归模型的预测

给定温度值，得到销售收入值

Temp = np.array([37])
Temp = Temp.reshape(-1,1)
Revenue = SimpleLinearRegression.predict(Temp)
print('Revenue Prediction = ',Revenue)

Revenue Prediction = [[837.90987079]]
即给定37度，得到837.91的销售收入。