秘密共享技术
尽管密码学提供了很多实用技术来保证信息安全，但是仅通过加密、解密、签名和认证等密码技术不能完整解决信息安全问题。原因在于加密等密码技术的核心是秘钥的安全保密，不是对算法或硬件本身的保护，而秘钥的安全性要求比一般数据高很多，仅通过加密等密码技术不足以达到其安全要求。因此秘密共享技术应运而生，为重要信息和秘密数据的安全存储与访问控制提供了有效的解决方法。其核心思想是将秘密进行适当地拆分，并由不同的参与者管理，单个参与者无法恢复秘密，只有若干个参与者协同才行恢复秘密。更重要的是当其中部分参与者出问题时，仍可以完整恢复秘密，使用秘密共享技术保管秘密具有以下优点：
（1）为秘密合理地创建副本，克服了“保存副本数量越多，安全性泄露的风险就越大，保存副本数量越少则副本丢失的风险越大”的矛盾
（2）有利于防止权力过于集中导致的被滥用问题
（3）不增加风险的情况下，增加了系统的可靠性
在分布式网络环境，尤其适合使用秘密共享技术来保证网络安全，并提高网络可靠性。下面介绍Shamir秘密共享技术。
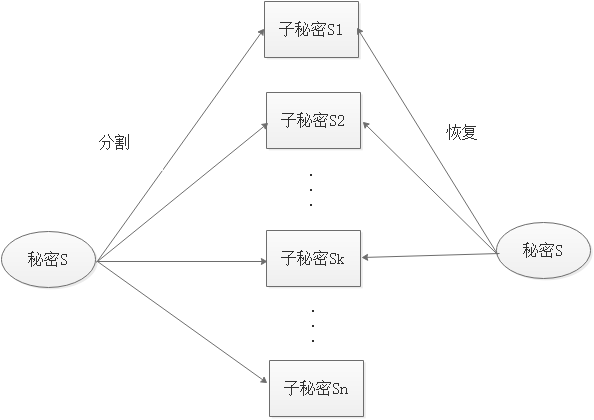
图1 Shamir的秘密共享基本原理
如图1所示为Shamir的秘密共享基本原理。秘密持有者将秘密S分为n个子秘密，只有拿到k个及以上子秘密才能成功恢复原始秘密S。这个k就是最少持有的可以恢复原始秘密的S的子秘密个数，称为门限值。少于k个子秘密都不能恢复原始秘密S。
Shamir的秘密共享的具体过程可分为三个阶段：初始化阶段、子秘密分发阶段和秘密恢复阶段。
（1）初始化阶段
秘密持有者随机从有限域GF(p)中选取n个不同发非零元素x1, x2, …xn标识每个子秘密持有者Pi(i=1,2,…,n)，同时公开xi。
（2）子秘密分发阶段
首先，秘密持有者要分发的秘密\(S\in Z_{q}\)，且q是一个大素数。然后，秘密持有者在GF(p)内任意选择k-1个元素aj（j=1,2,…,k-1）构成多项式
\[ h(x) = a_{k-1}x^{k-1}+\cdots +a_{1}x+a_{0} \: mod \: p \]
其中p是一个大素数且p>S，秘密\(S=h(0)=a_{0}\)。
最后，秘密持有者使用下面公式为所有子秘密持有者Pi生成n个子秘密Si，并将其发送给相应的Pi
\[S_{i}= h(x_{i})\: mod \: p \quad i = 1,\cdots ,n\]
（3）秘密恢复阶段
任何一个子秘密持有者只要拥有k个子秘密，就可以通过拉格朗日插值公式重构出秘密持有者构造的秘密分发多项式，进而恢复原始秘密S。
\[h(x) = \sum_{r=1}^{k}S_{i_{r}}\prod_{j\neq r,j=1}^{k}\frac{x-x_{i_{j}}}{x_{i_{r}-x_{i_{j}}}}\:mod \:p\]
